九年级(初三)数学下学期下册试题
如图,  是
是  的弦,C为
的弦,C为  上一点,过点C作
上一点,过点C作  的垂线与AB的延长线交于点D,连接
的垂线与AB的延长线交于点D,连接 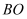 并延长,与
并延长,与  交于点E,连接EC,
交于点E,连接EC,  .
.
 是
是  的弦,C为
的弦,C为  上一点,过点C作
上一点,过点C作  的垂线与AB的延长线交于点D,连接
的垂线与AB的延长线交于点D,连接 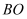 并延长,与
并延长,与  交于点E,连接EC,
交于点E,连接EC,  .
.

-
(1) 求证:CD是
 的切线;
的切线;
-
(2) 若
 ,
,  ,求
,求  的半径.
的半径.
-
(3) 在(2)的条件下,在线段AD上有一点P,连接
 、
、  ,则
,则  的最小值为.
的最小值为.
某校组织学生到恩格贝  和康镇
和康镇  进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,  和
和  分别位于学校
分别位于学校  的正北和正东方向,
的正北和正东方向,  位于
位于  南偏东37°方向,校车从
南偏东37°方向,校车从  出发,沿正北方向前往
出发,沿正北方向前往  地,行驶到15千米的
地,行驶到15千米的  处时,导航显示,在
处时,导航显示,在  处北偏东45°方向有一服务区
处北偏东45°方向有一服务区  ,且
,且  位于
位于  ,
,  两地中点处.
两地中点处.
 和康镇
和康镇  进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,  和
和  分别位于学校
分别位于学校  的正北和正东方向,
的正北和正东方向,  位于
位于  南偏东37°方向,校车从
南偏东37°方向,校车从  出发,沿正北方向前往
出发,沿正北方向前往  地,行驶到15千米的
地,行驶到15千米的  处时,导航显示,在
处时,导航显示,在  处北偏东45°方向有一服务区
处北偏东45°方向有一服务区  ,且
,且  位于
位于  ,
,  两地中点处.
两地中点处. 
(参考数据:  ,
,  ,
,  )
)
-
(1) 求
 ,
,  两地之间的距离;
两地之间的距离;
-
(2) 校车从
 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达  地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
某物体如图所示,它的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .
如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由  改为
改为  .已知原传送带
.已知原传送带  长为
长为  .
.
 改为
改为  .已知原传送带
.已知原传送带  长为
长为  .
. 
-
(1) 求新传送带
 的长度;
的长度;
-
(2) 如果需要在货物着地点
 的左侧留出
的左侧留出  的通道,试判断距离
的通道,试判断距离  点
点  的货物
的货物  是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
位于第一象限的点E在反比例函数y=  的图象上,点F在x轴的正半轴上,O是坐标原点.若EO=EF,△EOF的面积等于2,则k=( )
的图象上,点F在x轴的正半轴上,O是坐标原点.若EO=EF,△EOF的面积等于2,则k=( )
 的图象上,点F在x轴的正半轴上,O是坐标原点.若EO=EF,△EOF的面积等于2,则k=( )
的图象上,点F在x轴的正半轴上,O是坐标原点.若EO=EF,△EOF的面积等于2,则k=( )
A . 4
B . 2
C . 1
D . ﹣2
当45°<θ<90°时,下列各式中正确的是( )
A . tanθ>cosθ>sinθ
B . sinθ>cosθ>tanθ
C . tanθ>sinθ>cosθ
D . cosθ>sinθ>tanθ
如图,A,B是反比例函数  图象上的两点,过点A作
图象上的两点,过点A作  轴,垂足为C,AC交OB于点
轴,垂足为C,AC交OB于点  若D为OB的中点,
若D为OB的中点,  的面积为6,则k的值为
的面积为6,则k的值为
 图象上的两点,过点A作
图象上的两点,过点A作  轴,垂足为C,AC交OB于点
轴,垂足为C,AC交OB于点  若D为OB的中点,
若D为OB的中点,  的面积为6,则k的值为
的面积为6,则k的值为
面对新冠疫情,中国举全国之力采取了很多强有力的措施,将疫情及时控制,其中对感染者和接触者进行隔离治疗和观察有效地控制住病毒的传播,数学中为对两个图形进行隔离,在平面直角坐标系中,对“隔离直线”给出如下定义:点
 是图形
是图形
 上的任意一点,点
上的任意一点,点
 是图形
是图形
 上的任意一点,若存在直线
上的任意一点,若存在直线
 满足
满足
 且
且
 , 则称直线l:
, 则称直线l:
 是图形
是图形
 与
与
 的“隔离直线”.例如:如图1,直线l:
的“隔离直线”.例如:如图1,直线l:
 是函数图象与正方形的一条“隔离直线”.
是函数图象与正方形的一条“隔离直线”.
 是图形
是图形
 上的任意一点,点
上的任意一点,点
 是图形
是图形
 上的任意一点,若存在直线
上的任意一点,若存在直线
 满足
满足
 且
且
 , 则称直线l:
, 则称直线l:
 是图形
是图形
 与
与
 的“隔离直线”.例如:如图1,直线l:
的“隔离直线”.例如:如图1,直线l:
 是函数图象与正方形的一条“隔离直线”.
是函数图象与正方形的一条“隔离直线”.

-
(1) 在直线
 ,
,
 ,
,
 中,是图1函数
中,是图1函数
 的图象与正方形OABC的“隔离直线”的为;
的图象与正方形OABC的“隔离直线”的为;
-
(2) 如图2,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是
 ,
,
 与⊙O的“隔离直线”有且只有一条,求出此“隔离直线”的表达式;
与⊙O的“隔离直线”有且只有一条,求出此“隔离直线”的表达式;
-
(3) 正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点
 是此正方形的中心.若存在直线
是此正方形的中心.若存在直线
 是函数
是函数
 的图象与正方形A1B1C1D1的“隔离直线”,求t的取值范围.
的图象与正方形A1B1C1D1的“隔离直线”,求t的取值范围.
已知一个长方体的体积是100cm3 , 它的长是ycm,宽是10cm,高是xcm.
(1)写出y与x之间的函数关系式;
(2)当x=2cm时,求y的值.
已知线段a=4,b=9,线段c是a,b的比例中项,则线段c=。
三角形的面积为12cm2 , 把它的底y表示成这边上的高x的函数,那么表达式是 ,其图象位于第 象限.
在Rt△ABC中,∠C=90°,sinA= , 则tanA=
, 则tanA=
 , 则tanA=
, 则tanA=
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到的这个几何体的形状图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,扇形的圆心角为120°,半径为6,将此扇形围成一个圆锥,则圆锥的底面半径为.

已知:如图, 是
是 的直径C,D是
的直径C,D是 上两点,过点C的切线交
上两点,过点C的切线交 的延长线于点E,
的延长线于点E, , 连接
, 连接 .
.
 是
是 的直径C,D是
的直径C,D是 上两点,过点C的切线交
上两点,过点C的切线交 的延长线于点E,
的延长线于点E, , 连接
, 连接 .
. 
-
(1) 求证:
 ;
;
-
(2) 若
 , 求
, 求 的半径.
的半径.
某高速公路全长为  ,那么汽车行完全程所需的时间
,那么汽车行完全程所需的时间  与行驶的平均速度
与行驶的平均速度  之间的关系式为.
之间的关系式为.
 ,那么汽车行完全程所需的时间
,那么汽车行完全程所需的时间  与行驶的平均速度
与行驶的平均速度  之间的关系式为.
之间的关系式为.
如图,点M是反比例函数y=  (x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
 (x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( )
(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为( ) 
A . 1
B . 2
C . 4
D . 不能确定
计算:  = .
= .
 = .
= .
如图,在平面直角坐标系中,一次函数y=﹣  x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=  的图象在第一象限经过点A.
的图象在第一象限经过点A.
 x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=  的图象在第一象限经过点A.
的图象在第一象限经过点A.
-
(1) 求点A的坐标以及k的值:
-
(2) 点P是反比例函数y=
 (x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
下列关于y与x的表达式中,反映y是x的反比例函数的是( ).
A . y=4x
B .  =-2
C . xy=4
D . y=4x-3
=-2
C . xy=4
D . y=4x-3
 =-2
C . xy=4
D . y=4x-3
=-2
C . xy=4
D . y=4x-3
最近更新
- 只有在细胞保持活性的条件下,才能显示细胞中某物质或结构的实验是() ①用黑藻观察细胞质流动 ②用龙胆紫染色观察洋葱根尖分
- 人们将一种叫“水葫芦”的植物引种到昆明滇池后,这种植物很快在滇池中蔓延,甚至威胁到其它生物的生存.这说明了() A. 生
- All in all, the TV programmes were peaceful and entertaining
- 阅读下列材料:材料一1854年,当他(美国海军准将马修・佩里)再次来到日本时……日本人被迫让步,于3月31日签订了《神奈
- 下列关于水的说法,正确的是( ) A.通过看外观的方法检验硬水和软水 B.经过沉淀、过滤、活性炭吸附后得到的
- 中国学者所翻译的众所周知的“吾爱吾师,吾尤爱真理”是亚里士多德的名言,下列言论与之表达意思接近的是( ) A.真正的
- 阅读下面文章,完成12—16题。(15分)阅读的愉悦李国文古人说“开卷有益”,这是绝对真理。古人还说“敬惜字纸”,在他们
- 直接指导十月革命的纲领性文件是() A.《宣言》 B.《四月提纲》 C.《和平法令》
- 如图是用螺丝刀撬开饼干盒盒盖的情形,饼干盒盒盖难以撬开,是因为盖子和盒子之间_____较大,螺丝刀在撬开盒盖时,其功能相
- 小乐想利用两块电流表和阻值已知的电阻R0测量电阻Rx的阻值。小乐选择了满足实验要求的电源、电流表A1和A2,并连接了部分
- 一足球质量是0.7 kg,在它以5 m/s的水平速度经过某位置时,被运动员以10 m/s的水平速度反向踢回,球与球鞋的接
- 杜甫在《忆昔》中写道:“忆昔开元全盛日,小邑犹藏万家室。稻米流脂粟米白,公私仓廪俱丰实。”这一景象产生于谁统治时期(
- 近日,中国少数民族服饰及民族肖像画展在首都机场精彩亮相。由国内著名画家创作的少数民族肖像画惟妙惟肖地刻画了各民族鲜明、浓
- Across the United States, there are several places where two
- 新华网北京2009年8月11日电:肆虐的“莫拉克”台风重创海峡两岸部分地区,给两岸百姓造成严重的生命和财产损失。为了防止
- 氨气分子空间构型是三角锥形,而甲烷是正四面体形,这是因为 ( ) A、两种分子的中心原子杂化轨道
- 如图a所示,水平面上质量相等的两木块A、B,用以轻弹簧相连接,这个系统处于平衡状态,现用~竖直向上的力F拉动木块A,使木
- 如下图所示,19世纪英国与美国的产品平均年出口值(百万镑)经历了不断变化的过程。从这幅图表中,我们可以得出的主要结论是
- —How much sugar have you put in my coffee? It tastes so bitt
- 下列反应中生成物的总能量大于反应物总能量的是( ) A.氢气在氧气中燃烧 B.铁



