九年级(初三)数学下学期下册试题
如图,已知点A的坐标为(a,4)(其中a<-3),射线OA与反比例函数 的图象 交于点P,点B,C分别在函数
的图象 交于点P,点B,C分别在函数 的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
 的图象 交于点P,点B,C分别在函数
的图象 交于点P,点B,C分别在函数 的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
-
(1) 当a=-6,求线段AC的长;
-
(2) 当AB=BO时,求点A的坐标;
-
(3) 求证:
 .
.
一数学兴趣小组为了测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得A的仰角为30°,求树高.(结果精确到0.1米,参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)

如图几何体的俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .
下列四个图形能围成棱柱的有几个( )

A . 0个
B . 1个
C . 2个
D . 3个
反比例函数y=- 的图像在( )
的图像在( )
 的图像在( )
的图像在( )
A . 第一、二象限
B . 第二、三象限
C . 第一、三象限
D . 第二、四象限
如图,△ABC中,DE∥BC,  ,AE=2cm,则AC的长是( )
,AE=2cm,则AC的长是( )
 ,AE=2cm,则AC的长是( )
,AE=2cm,则AC的长是( ) 
A . 2cm
B . 4cm
C . 6cm
D . 8cm
在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,下列等式:①b=ccosB;②b=atanB;③a=csinA;④a=ccosB;⑤a=btanA;⑤a=bcotA,其中正确的有( )
A . 1 个
B . 2 个
C . 3个
D . 4个
如图,河坝的横断面AB的坡比是1:2,坝高BC=3米,则坡面AB的长度是米.

如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,  ≈1.7).
≈1.7).

在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距千米。(结果精确到0.1千米,参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732) 
已知函数y=  的图象经过点(-3,4).
的图象经过点(-3,4).
 的图象经过点(-3,4).
的图象经过点(-3,4).
-
(1) 求k的值,并在正方形网格中画出这个函数的图象;
-
(2) 当x取什么值时,函数的值小于0?
如图是由4个相同的小正方体组成的立体图形,它的俯视图为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:

-
(1) 求横档AD的长;
-
(2) 点C离地面的高度.(sin15°=0.26,cos15°=0.97,精确到1cm)
如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶点”的坐标为(a,﹣b),那么大“鱼”上对应“顶点”的坐标为.

如图,矩形ABCD∽矩形DEFC,且面积比为4:1,则AE:ED的值为( )

A . 4:1
B . 3:1
C . 2:1
D . 3:2
如图所示,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上任意一点,则PK+QK的最小值为( )

A . 1
B . 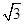 C . 2
D .
C . 2
D . 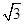 +1
+1
由5个相同的立方体搭成的几何体如图所示, 则它的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
由大小相同的小立方块搭成的几何体如下图,请你画出该几何体的左视图和俯视图.

如图,某飞机在空中A处探测到它的正下方地平面上目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=30°,则飞机A与指挥台B的距离为( )

A . 1200m
B .  C .
C .  D . 2400m
D . 2400m
 C .
C .  D . 2400m
D . 2400m
如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BD•CE,求证:△ABD∽△ECA.

最近更新
- 如图所示,放在水平桌面上的木块A(左右细线水平)处于静止状态,所挂的砝码和托盘的总质量为0.6kg,轻质的弹簧测力计的读
- 为避免“上有所措置,不能喻之民,下有所苦患,不能告之君,则有喉舌而无喉舌”而创办的报刊是 A.《时务
- ---Dothese paintings_______ you? ---No, they are not to m
- 若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角是 ( )A.30°
- 下列自然资源中属于非可再生资源的是( ) A.耕地 B.石油 C.水能
- 16.有学者认为:“古代雅典政治建立在一种非常不民主的基础之上。” 下列雅典民主政治鼎盛时期的史实,可以支持该论断的是
- 2.下列各句中,没有语病的一句是( ) A.中国探月工程已将圆满完成二期工程,转入三期;嫦娥五号作为探月三期工程“主
- 隋唐文化博大精深,对后世及世界文明都产生了深远的影响。隋唐对世界科技做出的重大贡献是( ) ①首次把火药用于军事
- 质检部门从某超市销售的甲、乙两种食用油中分划随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图: (I
- 下列有关生物多样性与生物进化的叙述中,不正确的是( ) A.细菌在接触青霉素后会产生抗药性的突变个体,青霉
- 古希腊著名哲学家赫拉克利特有一句名言:“世界是包括一切的整体,它不是由任何神或被任何人创造的,它的过去、现在和将来都是按
- 读“某厂建厂的地点与成本分析表”,据此回答57~58题。 57.从经济效益看,该厂最好建在( ) A.甲地
- 是西北地区的显著自然特征;青藏地区的显著自然特征是 。
- 如图所示,一半径为R的均匀带正电圆环水平放置,环心为O点,质量为m的带正电的小球从O点正上方h高的A点静止释放,并穿过带
- 在一座古墓中发现了黑亮如漆的黑陶,洁白如雪的白瓷,闻名中外的粉彩瓷和珐琅彩。这座墓葬的形成时间应不早于:A.魏晋
- 完形填空,阅读下列短文, 从每小题所给的A、B、C、D 四个选项中选出最佳选项。
- (四)阅读《旧餐桌上的美好时光》完成16——19题。(17分)旧餐桌上的美好时光 [美]凯瑟琳·比恩 (洪帆 译)一
- 在由N和O组成的化合物中,N和O的质量比为7:4,该化合物的化学式为( ) A、NO B、N2OC、NO2 D、N2O
- 在我国,人民是国家的主人。回答下列各题。 我国的全国人大代表,来自各地区、各民族和社会各个方面,工人、农民、知识分子、解
- 阅读理解William Shakespeare was a writer of plays and poems. Som



