九年级(初三)数学下学期下册试题
在数学实践活动课上,老师带领同学们到附近的公园测量园内一古楼的高度.测量方法如下:首先,用测角仪  在C处测得楼顶端
在C处测得楼顶端  点的仰角为
点的仰角为  ,然后,往古楼方向前进
,然后,往古楼方向前进  米至E处,测得楼顶端
米至E处,测得楼顶端  点的仰角为
点的仰角为  ,
,  .已知点B、E、C在一条直线上,
.已知点B、E、C在一条直线上,  ,
,  ,
,  ,测量示意图如图所示,请你求出该古楼的高度
,测量示意图如图所示,请你求出该古楼的高度  .(参考数据:
.(参考数据:  ,
,  ,
,  ,
,  ,
,  ,
,  )
)
 在C处测得楼顶端
在C处测得楼顶端  点的仰角为
点的仰角为  ,然后,往古楼方向前进
,然后,往古楼方向前进  米至E处,测得楼顶端
米至E处,测得楼顶端  点的仰角为
点的仰角为  ,
,  .已知点B、E、C在一条直线上,
.已知点B、E、C在一条直线上,  ,
,  ,
,  ,测量示意图如图所示,请你求出该古楼的高度
,测量示意图如图所示,请你求出该古楼的高度  .(参考数据:
.(参考数据:  ,
,  ,
,  ,
,  ,
,  ,
,  )
) 
若要使图中平面展开图按虚线折叠成正方体后,相对面上两个数互为相反数,则x+y=.

疫情期间,按照防疫要求,学生在进校时必须排队接受体温检测.某校统计了学生早晨到校情况,发现学生到校的累计人数y(单位:人)随时间x(单位:分钟)的变化情况如图所示,y可看作是x的二次函数,其图象经过原点,且顶点坐标为(30,900),其中0≤x≤30.校门口有一个体温检测棚,每分钟可检测40人.

-
(1) 求y与x之间的函数解析式;
-
(2) 校门口排队等待体温检测的学生人数最多时有多少人?
-
(3) 检测体温到第4分钟时,为减少排队等候时间,在校门口临时增设一个人工体温检测点.已知人工每分钟可检测12人,人工检测多长时间后,校门口不再出现排队等待的情况(直接写出结果).
下列四个关系式中,y是x的反比例函数的是( )
A . y=4x
B . y=  C . y=
C . y=  D . y=
D . y= 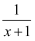
 C . y=
C . y=  D . y=
D . y= 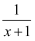
已知四边形ABCD的一组对边AD、BC的延长线交于点E.
-
(1) 如图1,若∠ABC=∠ADC=90°,求证:ED•EA=EC•EB;

-
(2) 如图2,若∠ABC=120°,cos∠ADC=
 ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
-
(3) 如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC=
 ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
如图,甲、乙两座建筑物的水平距离BC为80m,从甲的顶部A处测得乙的顶部D处的俯角为50°,测得底部C处的俯角为62°.求乙建筑物的高度DC.(结果取整数:参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)

已知:如图所示,在平面直角坐标系xOy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动.设点P、点Q的运动时间为t(s).

-
(1) 当t=1s时,求经过点O,P,A三点的抛物线的解析式;
-
(2) 当t=2s时,求tan∠QPA的值;
-
(3) 当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
-
(4) 连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.
图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):

-
(1) 图中虚线部分的长为 cm,俯视图中长方形的长为 cm;
-
(2) 求主视图中的弧所在圆的半径;
-
(3) 试计算该相框可插入的照片的最大面积(参考数据:sin22.5°≈
 ,cos22.5°≈
,cos22.5°≈  ,tan22.5°≈
,tan22.5°≈ 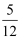 ,计算结果保留π).
,计算结果保留π).
如图,直线y=kx与双曲线  =-
=- 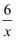 交于A、B两点,点C为第三象限内一点.
交于A、B两点,点C为第三象限内一点.
 =-
=- 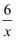 交于A、B两点,点C为第三象限内一点.
交于A、B两点,点C为第三象限内一点. 
-
(1) 若点A的坐标为(a,3),求a的值;
-
(2) 当k=-
 ,且CA=CB,∠ACB=90°时,求C点的坐标;
,且CA=CB,∠ACB=90°时,求C点的坐标;
-
(3) 当△ABC为等边三角形时,点C的坐标为(m,n),试求m、n之间的关系式.
对于反比例函数y  ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )
A . 图象经过点(2,1)
B . 图象位于第一、三象限
C . 当x<0时,y随x的增大而减小
D . 当x>0时,y随x的增大而增大
如图,在△ABC中,∠A=30°,∠B=45°,AC=  ,则AB的长为.
,则AB的长为.
 ,则AB的长为.
,则AB的长为. 
一个圆锥形零件,高为8cm,底面圆的直径为12cm,则此圆锥的侧面积是 cm2 .
由四个相同小立方体拼成的几何体如图所示,当光线由上向下垂直照射时,该几何体在水平投影面上的正投影是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .
对如图的几何体变换位置或视角,则可以得到的几何体是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC , AD=1,AB=3,那么  的值为( )
的值为( )
 的值为( )
的值为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,一次函数  的图象与
的图象与  轴、
轴、  轴分别交于点
轴分别交于点  ,
,  ,与反比例函数
,与反比例函数  (
(  )的图象交于点
)的图象交于点  ,
,  .
.
 的图象与
的图象与  轴、
轴、  轴分别交于点
轴分别交于点  ,
,  ,与反比例函数
,与反比例函数  (
(  )的图象交于点
)的图象交于点  ,
,  .
. 
-
(1) 分别求出两个函数的解析式;
-
(2) 连接
 ,求
,求  的面积.
的面积.
用小立方体搭一个几何体,使它从正面和上面看到的形状如图所示,从上面看到的形状中小正方形的字母表示在该位置上小立方块的个数,请问:

-
(1) b,c各表示几?答:b=,c=;
-
(2) 这个几何体最少由个小立方块搭成,最多由个小立方块搭成;
-
(3) 能搭出满足条件的几何体共有几种情况?其中从左面看该几何体的形状图共有多少种?请画出其中一种从左面看到的几何体的形状图.
一个圆柱体钢块,正中央被挖去了一个长槽,其俯视图如图所示,则此圆柱体钢块的左视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,△ABC、△FED分别为汽车两侧盲区的示意图,已知视线PB与地面BE的夹角∠PBE=43°,视线PE与地面BE的夹角∠PEB=20°,点A,F分别为PB,PE与车窗底部的交点,AF∥BE,AC,FD垂直地面BE,A点到B点的距离AB=1.6m,求盲区中DE的长度.(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)

如图,A、B是双曲线y=  上的点,点C在x轴上,B是线段AC的中点,
上的点,点C在x轴上,B是线段AC的中点,  .则k的值为( )
.则k的值为( )
 上的点,点C在x轴上,B是线段AC的中点,
上的点,点C在x轴上,B是线段AC的中点,  .则k的值为( )
.则k的值为( ) 
A . 3
B . 4
C . 6
D . 8
最近更新
- 读“我国某地区矿产和城市分布示意图”(图13),回答下列问题。(1)该地区优势矿产资源是_______________,
- 在水溶液中能大量共存,且加入过量稀硫酸既有沉淀生成又有气体生成的离子组是()。A.Ba2+、Fe3+、Cl-、B.Ba2
- 如图2,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为A.20°
- 20世纪70年代以来,日本要求与美国建立平等的伙伴关系,80年代又提出成为“政治大国”的目标,其根本原因是( ) A
- 下列化学名词书写正确的是( ) A.正丁稀 B.硝基笨 C.乙酸乙脂 D.氨基酸
- 3.下列语句中加点的词语,使用不正确的一项是() (3分) A. 只要上下一致,戮力同心,站在新的历史起点上,全省人民必
- 吴光玲在《闽东传统民居的地理经济选择及文化内涵》 一文中指出:中国传统民居中,堂屋是住宅的主体, 是宗法制家族的象征
- 阅读下面文段,概括其所揭示的哲理,不超过25个字。 有兄弟二人,年龄不过四五岁。由于卧室的窗户整天都是密闭的,他们认为
- 如图所示,为在“探究动能定理”的实验中小车在运动过程中打点计时器在纸带上打出的一系列的点,打点的时间间隔为0.02 s,
- —I can hardly hear the radio. Would you please ______. —Ye
- 甲、乙两种晶体(不含结晶水)的溶解度曲线如下图 所示。 (1)t2℃时将20 g甲加人100 g水中,充分搅拌
- (2012北京海淀期末)A、B两个可视为质点的小球带有同种电荷,在外力作用下静止于光滑的绝缘水平面上。A的质量为m,B的
- 氢氧化钠是一种重要的化工基础原料,广泛地应用于造纸、纺织、石油化工、印染等行业。氢氧化钠的俗名是 只写一
- 如图所示,下列情况下线圈中不能产生感应电流的是( ) A.导线中的电流增加 B.线圈向右平动
- 下图是实验室制取并探究二氧化碳性质的实验装置: (1)仪器名称:A E
- (本题满分12分)已知直三棱柱ABC-A1B1C1的侧棱长与 底面三角形的各边长都等于a,点D为BC的中点. 求证:(1
- 图片展示: (1)你能说出下图中展示的服饰分别属于我国的哪个民族吗,请填在图片下方的横线上.
- 下列实验操作正确的是
- 某教师在历史教学过程中,要求学生举例说明和平与发展之间的辩证关系。下面是学生所举的例子,不对的是( ) A.欧盟的成
- 下面四条直线中,直线上每个点的坐标都是方程x-2y=2的解的是 ( ) A.



