九年级(初三)数学下学期下册试题
反比例函数y=  的图象经过( )象限.
的图象经过( )象限.
 的图象经过( )象限.
的图象经过( )象限.
A . 一、二
B . 一、三
C . 二、三
D . 二、四
随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起,高铁大大缩短了时空距离,改变了人们的出行方式,如图A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道由A地到O地,再由O地到B地可大大缩短路程、∠OAC=45°,∠OBC=60°,∠ACB=90°,AC=540公里,BC=400公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:  ≈1.7,
≈1.7,  ≈1.4,
≈1.4,  ≈2.4)
≈2.4)
 ≈1.7,
≈1.7,  ≈1.4,
≈1.4,  ≈2.4)
≈2.4)

计算:tan45°﹣2cos60°=.
若点P在线段AB上,点Q在线段AB的延长线上,AB=10, . 求线段PQ的长.
. 求线段PQ的长.
 . 求线段PQ的长.
. 求线段PQ的长.
如图,等腰  的顶角
的顶角  ,请用尺规作图法,在
,请用尺规作图法,在  边上求作一点
边上求作一点  ,使得
,使得  ∽
∽  .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
 的顶角
的顶角  ,请用尺规作图法,在
,请用尺规作图法,在  边上求作一点
边上求作一点  ,使得
,使得  ∽
∽  .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法) 
在平面直角坐标系xOy中,A为双曲线  上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )
上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )
 上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )
上一点,点B的坐标为(4,0).若△AOB的面积为6,则点A的坐标为( )
A . ( 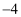 ,
,  )
B . (4,
)
B . (4,  )
C . (
)
C . ( 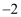 ,3)或(2,
,3)或(2,  )
D . (
)
D . (  ,2)或(3,
,2)或(3, 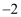 )
)
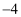 ,
,  )
B . (4,
)
B . (4,  )
C . (
)
C . ( 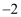 ,3)或(2,
,3)或(2,  )
D . (
)
D . (  ,2)或(3,
,2)或(3, 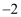 )
)
若点(-2,  ),(-1,
),(-1,  ),(1,
),(1,  )在反比例函数
)在反比例函数 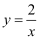 的图像上,则下列结论中,正确的是( )
的图像上,则下列结论中,正确的是( )
 ),(-1,
),(-1,  ),(1,
),(1,  )在反比例函数
)在反比例函数 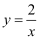 的图像上,则下列结论中,正确的是( )
的图像上,则下列结论中,正确的是( )
A .  >
>  >
>  B .
B .  >
>  >
>  C .
C .  >
>  >
>  D .
D .  >
>  >
> 
 >
>  >
>  B .
B .  >
>  >
>  C .
C .  >
>  >
>  D .
D .  >
>  >
> 
如图,甲、乙、丙图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )

A . 仅有甲和乙相同
B . 仅有甲和丙相同
C . 仅有乙和丙相同
D . 甲、乙、丙都相同
2022年2月4日晚,当我国运动员迪妮格尔·衣拉木江和赵嘉文将最后一棒火炬嵌入主火炬“大雪花”中央时,第24届北京冬奥会向世界展示了低碳环保的“点火”仪式,小华有幸在现场目睹这一过程,在“大雪花”竖直升起的某一刻,从小华的位置(点O)观测“大雪花”的顶部A的仰角 为12.8°,底部B的俯角β为15.3°,已知“大雪花”高AB约14.89 m,求小华的位置离“大雪花”的水平距离OC.(结果精确到0.1 m,参考数据: tan12.8°
为12.8°,底部B的俯角β为15.3°,已知“大雪花”高AB约14.89 m,求小华的位置离“大雪花”的水平距离OC.(结果精确到0.1 m,参考数据: tan12.8° 0.23,sin12.8°
0.23,sin12.8° 0.22,tan15.3°
0.22,tan15.3° 0.27,sin15.3°
0.27,sin15.3° 0.26)
0.26)
 为12.8°,底部B的俯角β为15.3°,已知“大雪花”高AB约14.89 m,求小华的位置离“大雪花”的水平距离OC.(结果精确到0.1 m,参考数据: tan12.8°
为12.8°,底部B的俯角β为15.3°,已知“大雪花”高AB约14.89 m,求小华的位置离“大雪花”的水平距离OC.(结果精确到0.1 m,参考数据: tan12.8° 0.23,sin12.8°
0.23,sin12.8° 0.22,tan15.3°
0.22,tan15.3° 0.27,sin15.3°
0.27,sin15.3° 0.26)
0.26)
如图,点 A 在以
BC 为直径的⊙O 内,且
AB=AC,以点 A 为圆心,AC 长为半径作弧, 得到扇形 ABC,剪下扇形 ABC 围成一个圆锥(AB 和 AC 重合),若∠ABC=30°, BC = 2  ,则这个圆锥底面圆的半径是.
,则这个圆锥底面圆的半径是.
 ,则这个圆锥底面圆的半径是.
,则这个圆锥底面圆的半径是. 
如图是一个正方体纸盒的展开图,请把  分别填入六个正方形,使得折成正方体后,相对面上的两数互为相反数(填出其中一种即可).
分别填入六个正方形,使得折成正方体后,相对面上的两数互为相反数(填出其中一种即可).
 分别填入六个正方形,使得折成正方体后,相对面上的两数互为相反数(填出其中一种即可).
分别填入六个正方形,使得折成正方体后,相对面上的两数互为相反数(填出其中一种即可). 
方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
-
(1) 求v关于t的函数表达式;
-
(2) 方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
如图,在△ABC中,点D,E,F分别在边AB、AC、BC上,DE∥BC,DF∥AC,已知  =
=  .
.
 =
=  .
.

-
(1) 求
 的值.
的值.
-
(2) 若△ADE的面积为4,求△ABC的面积.
如图所示的物体的左视图为( )

A . 
B .
B . 
C .
C .  D .
D . 

B .
B . 
C .
C .  D .
D . 
已知直线:y1=  与x轴、y轴相交于A、B两点,与双曲线
与x轴、y轴相交于A、B两点,与双曲线  (k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为
(k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为  ,且B是AC的中点.
,且B是AC的中点.
 与x轴、y轴相交于A、B两点,与双曲线
与x轴、y轴相交于A、B两点,与双曲线  (k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为
(k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为  ,且B是AC的中点.
,且B是AC的中点.

-
(1) 求k的值;
-
(2) 直接写出
 的解集;
的解集;
-
(3) 若P为直线l的一动点,点P的纵坐标为m,∠APB≥30°,求m的范围.
京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).

在平面直角坐标系中有两点A(6,2),B(6,0),以原点为位似中心,相似比为1∶3.把线段AB缩小,则过A点对应点的反比例函数的解析式为( )
A .  B .
B .  C .
C .  D .
D . 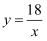
 B .
B .  C .
C .  D .
D . 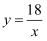
用科学计算器计算:7  ﹣5sin37°=(结果精确到0.1).
﹣5sin37°=(结果精确到0.1).
 ﹣5sin37°=(结果精确到0.1).
﹣5sin37°=(结果精确到0.1).
如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

-
(1) 请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
-
(2) 如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
为了测量悬停在空中A处的无人机的高度,小明在楼顶B处测得无人机的仰角为45°,小丽在地面C处测得A、B的仰角分别为56°、14°.楼高BD为20米,求此时无人机离地面的高度.(参考数据:tan14°≈0.25,tan56°≈1.50)

最近更新
- 某密闭容器中进行如下反应:X(g)+2Y(g) 2Z(g),若最初时只加入X、Y两种物质,要使平衡时反应物总物质的量与
- 在矩形ABCD中,AB=a,AD=2b,a<b,E、F分别是AD、BC的中点,以EF为折痕把四边形EFCD折起,当
- 对下面两首词的分析,不恰当的一项是破阵子(辛弃疾)醉里挑灯看剑,梦回吹角连营。八百里分麾下炙,五十弦翻塞外声,沙场秋点兵
- 2010年7月1日《侵权责任法》正式实施,人民的合法权益又多了一层法律保障,这表明( ) A.社会主义民主具有真实性
- 读“中国四大地理分区图“,回答下列问题(10分)(1)北方地区与南方地区的界线是 ______ (山脉)— _
- 已知α∈(,π),sinα=,则tan(α+)等于A. B.7
- (2009年山东理综)人类常染色体上β??珠蛋白基因 (A+)既有显性突变(A)又有隐性突变(a),突变均可导致地中海贫
- 在如图所示的装置中,两个光滑的定滑轮的半径很小,表面粗糙的斜面固定在地面上,斜面的倾角为θ=30°。用一根跨过定滑轮的细
- —Lucy,I told Denny about your success.—Oh,you ________ him;I
- 在对流层中,气温随高度的增加而减小,当地面气温上升至0℃以上时,在高空中则会出现0℃层,此时0℃层所对应的海拔高度就是气
- 政府机关是我国的行政机关,它与人民群众的关系最为密切。回答 依法行政是依法治国的重要环节。依法行政,就是要求 ①各级党组
- .某地区有荒山2200亩,从2002年开始每年年初在荒山上植树造林, 第一年植树100亩,以后每年比上一年多植树50亩.
- 已知.若关于的方程 有三个不同的实数解,则的取值范围是 (
- 为了连续改变反射光的方向,并多次重复这个方向,方法之一是旋转由许多反射镜面组成的多面体棱镜(简称镜鼓)。如图所示,当激光
- 下列四句话不能够体现我国地理位置优越性的是:( ) A.自西向东流淌的大河沟通了我国东西方的交通,方便了内陆与沿
- 某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天
- 下列过程中属于液化的是 A.积水干涸 B.大雾弥漫
- 2010年1月11日,中共中央、国务院在北京隆重举行国家科学技术奖励大会,_____和_____获得2009年度国家最高
- (北京理综)新生儿小肠上皮细胞通过消耗ATP,可以直接吸收母乳中的免疫球蛋白和半乳糖。这两种物质分别被吸收到血液中的方式
- 中国诗词、成语和谚语中有些蕴含着化学知识。下列说法正确的是( ) A.“遥知不是雪,为有暗香来”说明分子在不断地运动



