九年级(初三)数学下学期下册试题
如下图,以某点为位似中心,将△AOB进行位似变换得到△CDE,记△AOB与△CDE对应边的比为k,则位似中心的坐标和k的值分别为( )

A .  B .
B .  C .
C .  D .
D . 
如图,A.B是双曲线y=  上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为.
上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为. 
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的主视图和左视图.

三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在  中,
中,  ,
,  为
为  上一点,
上一点,  ,点
,点  从点
从点  出发,沿
出发,沿  方向以
方向以  的速度匀速运动,同时点
的速度匀速运动,同时点  由点
由点  出发,沿
出发,沿 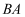 方向以
方向以  的速度匀速运动,设运动时间为
的速度匀速运动,设运动时间为  ,连接
,连接  交
交 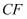 于点
于点  ,若
,若  ,则
,则  的值为( )
的值为( )
 中,
中,  ,
,  为
为  上一点,
上一点,  ,点
,点  从点
从点  出发,沿
出发,沿  方向以
方向以  的速度匀速运动,同时点
的速度匀速运动,同时点  由点
由点  出发,沿
出发,沿 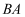 方向以
方向以  的速度匀速运动,设运动时间为
的速度匀速运动,设运动时间为  ,连接
,连接  交
交 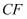 于点
于点  ,若
,若  ,则
,则  的值为( )
的值为( ) 
A . 1
B . 2
C . 3
D . 4
如图,添加一个条件:,使△ADE∽△ACB,(写出一个即可)

如图,  中,
中,  于点D,若
于点D,若  ,
,  ,则
,则  的值为( )
的值为( )
 中,
中,  于点D,若
于点D,若  ,
,  ,则
,则  的值为( )
的值为( ) 
A .  B .
B .  C .
C . 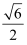 D .
D . 
 B .
B .  C .
C . 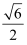 D .
D . 
市政府计划建设一项水利工程,工程需要运送的土石方总量为106立方米,某运输公司承担了运送土石方的任务.设该公司平均每天运送土石方总量为y立方米,完成运送任务所需时间为t天.
-
(1) 求y关于t的函数表达式;
-
(2) 当y=1000时,求t的值;
-
(3) 若工期要求在100天内完成,公司每天至少要运送多少立方米土石方?
如图,已知抛物线 经过
经过 和
和 两点,直线
两点,直线 与x轴相交于点C,P是直线
与x轴相交于点C,P是直线 上方的抛物线上的一个动点,
上方的抛物线上的一个动点, 轴交
轴交 于点D.
于点D.
 经过
经过 和
和 两点,直线
两点,直线 与x轴相交于点C,P是直线
与x轴相交于点C,P是直线 上方的抛物线上的一个动点,
上方的抛物线上的一个动点, 轴交
轴交 于点D.
于点D.
-
(1) 求该抛物线的表达式;
-
(2) 若
 轴交
轴交 于点E,求
于点E,求 的最大值;
的最大值;
-
(3) 若以A,P,D为顶点的三角形与
 相似,请直接写出所有满足条件的点P,点D的坐标.
相似,请直接写出所有满足条件的点P,点D的坐标.
如图,将∠AOB放置在5×5的正方形网格中,则tan∠AOB的值是( )

A . 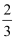 B .
B .  C .
C .  D .
D . 
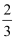 B .
B .  C .
C .  D .
D . 
如图,在Rt△ABC , ∠BAC=90°,AD⊥BC , AB=10,BD=6,则BC的值为( )

A .  B . 2
B . 2  C .
C .  D .
D . 
若一个圆锥的底面半径为5cm,其侧面展开图的圆心角为120°,则圆锥的母线长是cm.
如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.

-
(1) 求斜坡CD的高度DE;
-
(2) 求大楼AB的高度(结果保留根号)
如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).

-
(1) 以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′(,),C′(,);
-
(2) 在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标(,).
4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道4处的俯角为30°,启处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A,D.B在同一直线上,则AB两点的距离是米.

-
(1) 计算:
 ;
;
-
(2) 先化简,再求值:
 ,其中
,其中  .
.
用小立方块搭一几何体,使得它的从正面看和从上面看形状图如图所示,这样的几何体最少要个立方块,最多要个立方块.

如图,某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=60m,山坡的坡比为1:2.

-
(1) 求该建筑物的高度(即AB的长,结果保留根号);
-
(2) 求此人所在位置点P的铅直高度(即PD的长,结果保留根号).
如图,已知  ,
,  ,
,  ,
,  ,
,  .求AB的长.
.求AB的长.
 ,
,  ,
,  ,
,  ,
,  .求AB的长.
.求AB的长. 
如图:已知点A、B是反比例函数y=﹣ 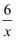 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为.
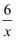 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为. 
最近更新
- 指出函数f(x)=的单调区间,并比较f(-π)与f(-)的大小.
- 小船以一定的速率垂直河岸向对岸划去,当水流匀速时,它渡河的时间、发生的位移与水速的关系是 ……( )A.水速小时,
- It’s the time of year when graduates are looking forward top
- The students were encouraged _______ English in class. A. sp
- 黎明时我们又起身出发了。(dawn;set off)
- 中央经济工作会议把扩大内需作为2009年经济工作的主要着力点之一。影响居民消费的主要因素是 ①居民收入水平 ②物价总
- 关于人体内水和无机盐平衡的调节的叙述中,正确的是( ) A.血浆渗透压降低时,引起口渴 B.机体失水时,
- PART TWO LANGUAGE KNOWLEDGE SECTION A Directions: Beneath
- Sorry, the other rooms have been rented, and this is the onl
- 根据课文默写古诗文。(10分) (1)绿树村边合, 。(孟浩然《过故人庄》)(1分) (2)
- 下列反应的离子方程式错误的是 ( ) A.等物质的量的Ba (OH)2与NH4HSO4在溶液中反应:Ba2++2O
- 1762年,约翰·威尔克斯开始发行《苏格兰人》报,其中第45期刊出一篇文章,激烈 谴责政府的对外政策,并对乔治三世本人进
- 图5是西汉政府授予边疆民族首领的铜质官印的印文,该印出土于新疆沙雅什格提遗址。这印证了当时这一地区( )A.与西汉王朝
- 逻辑推理是学习化学的一种重要方法.以下推理合理的是( ) A.H2O和H2O2的组成元素相同,所以它们的化学性质
- (08重庆卷)下列叙述错误的是 A.酵母菌有核膜,而固氮菌没有 B.酵母菌有细胞膜,而固氮菌没有
- (2010·福建厦门外国语学校高三第一次月考) 29. The thief ran away when the
- 下图中CH线为晨昏线。完成1~2题。1.能反映北半球冬季的是
- “日本文化其实是中国文化的新阐释,事实上并没有离开中国文化的根。”(《从历史看时代转移》)这种“新阐释”最早可以追溯到以
- 碳和部分碳的化合物间转化关系如图所示. (1)物质X的化学式为. (2)在物质的分类中,CO属于.(填标号) A.酸
- Those days Mr Zhang alwaysfelt stressed. He always dreamt ab



