九年级(初三)数学下学期下册试题
小明乘车从县城到怀化,行车的速度 和行车时间
和行车时间 之间函数图是( )
之间函数图是( )
 和行车时间
和行车时间 之间函数图是( )
之间函数图是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,已知二次函数y=﹣  (x+1)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则
(x+1)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则  的最小值为( )
的最小值为( )
 (x+1)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则
(x+1)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则  的最小值为( )
的最小值为( ) 
A .  B . 2
C .
B . 2
C .  D .
D . 
 B . 2
C .
B . 2
C .  D .
D . 
如果y与x﹣2成反比例函数,且比例系数k≠0,则它的函数解析式是,若x=3时,y=4,则k=.
如图,  内接于
内接于  ,
,  ,
,  ,
,  于点
于点  ,若
,若  的半径为4,则
的半径为4,则  的长为.
的长为.
 内接于
内接于  ,
,  ,
,  ,
,  于点
于点  ,若
,若  的半径为4,则
的半径为4,则  的长为.
的长为. 
如图,为测量楼CD的高度,从楼AB的顶点A测得楼CD的顶部点D的仰角为45°,底部C的俯角为30°,已知楼AB的高为30米,求楼CD的高度.

如图,在Rt△ABC中,∠C=90°,AC=BC,BC∥x轴,点A、B都在反比例函数y= 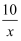 (x>0)上,点C在反比例函数y=
(x>0)上,点C在反比例函数y= 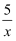 (x>0)上,则AB=.
(x>0)上,则AB=.
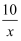 (x>0)上,点C在反比例函数y=
(x>0)上,点C在反比例函数y= 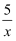 (x>0)上,则AB=.
(x>0)上,则AB=. 
如图所示的圆柱,其俯视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列各图不是正方体表面展开图的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D . 
图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.

-
(1) 请画出这个几何体的俯视图;
-
(2)
图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).

在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=6cm,高OC=8cm.则这个圆锥漏斗的侧面积是.

如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.

tan30°的值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m .
-
(1) 求动力F与动力臂l的函数解析式;
-
(2) 当动力臂为1.5m时,撬动石头至少需要多大的力?
如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα= 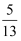 ,则小车上升的高度是( )
,则小车上升的高度是( )
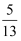 ,则小车上升的高度是( )
,则小车上升的高度是( ) 
A . 5米
B . 6米
C . 6.5米
D . 7米
如图,双曲线y=  的一个分支为( )
的一个分支为( )
 的一个分支为( )
的一个分支为( ) 
A . ①
B . ②
C . ③
D . ④
函数y=x+  的图象如图所示,下列对该函数性质的论断不可能正确的是( )。
的图象如图所示,下列对该函数性质的论断不可能正确的是( )。
 的图象如图所示,下列对该函数性质的论断不可能正确的是( )。
的图象如图所示,下列对该函数性质的论断不可能正确的是( )。
A . 该函数的图象是中心对称图形
B . y的值不可能为1
C . 在每个象限内,y的值随x值的增大而减小
D . 当x>0时,该函数在y时取得最小值2
如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D,过点D作DE∥AB交CA延长线于点E,连接AD,BD.

-
(1) △ABD的面积是多少
-
(2) 求证:DE是⊙O的切线:
-
(3) 求线段DE的长.
宽与长的比是  (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
 (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( ) 
A . 矩形ABFE
B . 矩形EFCD
C . 矩形EFGH
D . 矩形DCGH
2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( ) 

A .  米
B . m•tan(α﹣β)米
C . m(tanα﹣tanβ)米
D .
米
B . m•tan(α﹣β)米
C . m(tanα﹣tanβ)米
D .  米
米
 米
B . m•tan(α﹣β)米
C . m(tanα﹣tanβ)米
D .
米
B . m•tan(α﹣β)米
C . m(tanα﹣tanβ)米
D .  米
米
图①、图②、图③都是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,请在所给网格区域(含边界)上按要求画格点三角形.

-
(1) 在图①、图②中分别画一个△PAB,使△PAB的面积等于4(所画的两个三角形不全等).
-
(2) 在图③中,画一个△PAB,使tan∠APB=
 .
.
最近更新
- 2010年5月21日,全国公安机关召开反腐倡廉建设电视电话会议。要求全国公安机关集中解决公安执法和内部管理中群众反映最强
- 右图是某生物研究小组在“探究果酒制作过程中酵母菌种群数量变化因素”时,获得的两组实验数据(图中O、M、N、P代表相应发酵
- 据报道,英国科学家从人的皮肤细胞中提取出细胞核,植入剔除了细胞核的牛卵细胞中,从而培育出人兽混合胚胎。从遗传学角度米看,
- 电动势为E,内阻为的电池与固定电阻,可变电阻R串联,如图所示,设,,当变阻器的滑动片自端向端滑动时,下列物理量中随之减小
- 社会上不断发生“地沟油”、“皮革奶”、“瘦肉精”、 “染色馒头”等恶性食品安全事件足以表明,道德的滑坡已经到了严重的地步
- 在比较洋务运动和明治维新时,有人认为:“中国变了,但变的是皮毛,不变的是体制。跟着,日本也变了,但先变的是体制,然后是皮
- “打倒列强,除军阀。努力国民革命,齐奋斗”。这首歌诞生于下列哪一时期 A.辛亥革命
- 唐朝中央政府具有较高的行政效率,主要原因在于 A.增设机构,独立施政 B.分工明确,相互协调 C.一职多
- 下列现象属于渗透作用的是 A.水分子通过细胞壁 B.干大豆种子泡
- 下列五种物质中均含有氮元素,它们是按氮元素的化合价由低到高的顺序排列的:①NH3;②N2;③NO;④X;⑤N2O5。根据
- “华盛顿会议给中国造成一种新局面,就是历来各帝国主义者的互竞侵略,变为协同的侵略,这种协同的侵略,将要完全剥夺中国人民的
- 溶液在生活和生产中应用广泛。(1)下列物质中,属于溶液的是 。A.糖水B.牛奶C.碘酒D.汽油(2)配制200
- 有两个实验小组的同学为探究过氧化钠与二氧化硫的反应,都用如下图所示的装置进行实验。通入SO2气体,将带余烬的木条插入试管
- 下列有关C4和C3植物的描述中,错误的是( ) A.C3植物维管束鞘细胞中含有叶绿体 B.C4植物维管束鞘细胞中含
- 用托盘天平称量固体药品时,右边盘上放被称量物品,左边盘上砝码为10g,游码在标尺上0.3g处,天平平衡,则称量物的实际质
- 对下列实验过程的评价,正确的是 () A.某无色溶液滴入紫色石蕊试液显红色,该溶液一定显碱性 B.验证烧碱溶液中是否含有
- (08年新建二中三模) 已知二面角是直二面角,,设与所成的角分别是,则( ). A. B.
- 赤潮(由于海水中各种有机物、无机营养盐过量,导致海水富营养化而产生的一种有害的生态异常现象)频繁多发的海域是( )
- 组成细胞膜的主要成分是 A.磷脂、糖类; B.磷脂、蛋白质; C.磷脂、无机盐; D.磷脂
- Whocan tell me if there is a bookstall around Ican



