九年级(初三)数学：上学期上册　　 下学期下册

九年级(初三)数学下学期下册试题

如图，点A、B是双曲线y＝ $\text{[math]}$ 上的点，分别经过A、B两点向x轴、y轴作垂线段，若S_阴影＝1，则S₁+S₂＝.

图片_x0020_100002

某市教育行政部门为了了解初二学生每学期参加综合实践活动的情况，随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了如图1的两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:

（1）求出扇形统计图中的a的值以及对应的圆心角度数.
（2）补全图1的频数分布直方图.
（3）如果全市共有初二学生8000人，请你估计每学期参加综合实践活动时间不少于4天的大约是多少人?

计算

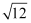2 $\text{[math]}$ °－ $\text{[math]}$ － $\text{[math]}$ ＋ $\text{[math]}$

如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：

（1）求点N的坐标（用含x的代数式表示）
（2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？
（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．

如图，已知△ABC和△A′B′C′相似，则图中角度 $\text{[math]}$ 和边长x分别为（）

A . 30°，9 B . 30°，6 C . 40°，9 D . 40°，6

（1）计算： $\text{[math]}$
（2）先化简，再求值： $\text{[math]}$ ，其中m=﹣6.

古希腊数学家、天文学家泰勒斯曾在金字塔影子的顶部立一根木杆，借助太阳光线利用数学原理，来测量金字塔的高度．如图，在某一时刻，测得木杆EF的长为2m，它的影长FD为3m，同时测得OA为201 m，求金字塔的高度BO．在解决这个问题的过程中，主要运用的数学知识是（）

A . 图形的轴对称 B . 图形的平移 C . 图形的旋转 D . 图形的相似

（1）【基础巩固】
如图1，在△ABC中，D，E，F分别为AB，AC，BC上的点，DE∥BC，BF=CF，AF交DE于点G，求证：DG= EG．
（2）【尝试应用】
如图2，在(1)的条件下，连结CD，CG．若CG⊥DE，CD=6，AE=3，求 $\text{[math]}$ 的值．
（3）【拓展提高】
如图3，在▱ABCD中，∠ADC=45°，AC与BD交于点O，E为AO上一点，EG∥BD交AD于点G，EF⊥EG交BC于点F．若∠EGF=40°，FG平分∠EFC，FG=10，求BF的长．

如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为 $\text{[math]}$ ，AC=2，则sinB的值是( ）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

如图，图1为一个长方体，AB=AD=16，AE=6，图2为左图的表面展开图，请根据要求回答问题：

（1）面“学”的对面是面什么？

（2）图1中，M、N为所在棱的中点，试在图2中画出点M、N的位置；并求出图2中△ABN的面积．

某班数学老师结合中国

建党一百周年，在班级内组织了一堂“正方体展开图猜猜看”活动课，下图是该正方体展开图的一种，那么原正方体中，与“建”字所在面对面上的汉字是（）

A . 礼 B . 年 C . 百 D . 赞

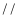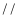如图，在 $\text{[math]}$ ABC中，DE $\text{[math]}$ BC，若AD：DB＝3：2，DE＝6cm，则BC的长为（　　）

A . 8cm B . 10cm C . 12cm D . 18cm

若一个三角形三个内角度数的比为1：2：3，那么这个三角形最小角的正切值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

如图，点A、B在反比例函数y＝ $\text{[math]}$ （k≠0）的图象上，过点A、B作x轴的垂线，垂足分别为M.N，延长线段AB交x轴于点C，若OM＝MN＝NC，四边形AMNB的面积为6，k的值为.

如图，A是反比例函数y= $\text{[math]}$ 的图象上一点，AB⊥y轴于点B．若△ABO面积为2，则k为值为（　　）

A . -4 B . 1 C . 2 D . 4

反比例函数y=

，当y≤3时，x的取值范围是 .

如图所示的几何体是由4个大小相同的小正方体搭成的，它的左视图是（）

A .

B .

C .

D .

如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．

（1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
（2）先化简，再求值： $\text{[math]}$ ．

已知反比例函数 $\text{[math]}$ 的图象经过点P（3，2），则下列各点在这个函数图象上的是（）

A . （-3，-2） B . （3，-2） C . （2，-3） D . （-2，3）

如图，在△ABC中，∠C=90°，AB=10，BC=8，P、Q分别是AB、BC边上的点，且AP=BQ=a （其中0＜a＜8）．

（1）若PQ⊥BC，求a的值；
（2）若PQ=BQ，把线段CQ绕着点Q旋转180°，试判别点C的对应点C’是否落在线段QB上？请说明理由．

最近更新

　