九年级(初三)数学下学期下册试题
一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为 .

如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P,Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值.

如图,有一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB,AC上,则这个正方形零件的边长为

A . 40mm
B . 45mm
C . 48mm
D . 60mm
如图是一个正方体的平面展开图,每个面上都标有一个汉字,将其折成一个正方体,与“起”字相对的面上的汉字为( )

A . 走
B . 向
C . 未
D . 来
下面两个三角形一定相似的是( )
A . 两个等腰三角形
B . 两个直角三角形
C . 两个钝角三角形
D . 两个等边三角形
如图,一次函数为y1=kx+b(k≠0)的图象与反比例函数y2=  (m≠0)的图象交于A(1,t+1),B(t﹣5,﹣1)两点,当y1>y2时,自变量x的取值范围为.
(m≠0)的图象交于A(1,t+1),B(t﹣5,﹣1)两点,当y1>y2时,自变量x的取值范围为.
 (m≠0)的图象交于A(1,t+1),B(t﹣5,﹣1)两点,当y1>y2时,自变量x的取值范围为.
(m≠0)的图象交于A(1,t+1),B(t﹣5,﹣1)两点,当y1>y2时,自变量x的取值范围为. 
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为.

如图,在边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( )

A .  B .
B .  C .
C .  D .
D . 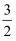
 B .
B .  C .
C .  D .
D . 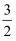
如图,在△ABC中,∠C=90°,AB=10,BC=8,则sin∠A=( )

A .  B .
B .  C .
C .  D .
D . 
已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积为
若反比例函数  的图象在第二、四象限,m的值为.
的图象在第二、四象限,m的值为.
 的图象在第二、四象限,m的值为.
的图象在第二、四象限,m的值为.
-
(1) 先化简,再求值:(2﹣
 )÷
)÷  ,其中x=2.
,其中x=2.
-
(2) 计算:|
 ﹣2|+20100﹣(﹣
﹣2|+20100﹣(﹣  )﹣1+3tan30°.
)﹣1+3tan30°.
图中立体图形的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
用“<”符号连接下列各三角函数cos15°、cos30°、cos45°、cos60°、cos75°.
如图,在边长为1正方形ABCD中,点P是边AD上的动点,将△PAB沿直线BP翻折,点A的对应点为点Q,连接BQ、DQ.则当BQ+DQ的值最小时,tan∠ABP=.

如图,在直角坐标系中,点A在第一象限内,点B在x轴正半轴上,以点O为位似中心,在第三象限内与ΔOAB的位似比为  的位似图形ΔOCD.若点C的坐标为
的位似图形ΔOCD.若点C的坐标为  ,则点A的坐标为( )
,则点A的坐标为( )
 的位似图形ΔOCD.若点C的坐标为
的位似图形ΔOCD.若点C的坐标为  ,则点A的坐标为( )
,则点A的坐标为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是 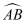 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )

A . (sinα,sinα)
B . (cosα,cosα)
C . (cosα,sinα)
D . (sinα,cosα)
-
(1) 计算:4sin60°﹣
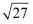 +(
+(  ﹣1)0;
﹣1)0;
-
(2) 化简:(x+y)2﹣(x﹣y)(x+y).
为了丰富学生社会实践活动,学校组织学生到红色文化基地 和人工智能科技馆
和人工智能科技馆 参观学习.如图,学校在点
参观学习.如图,学校在点 处,
处, 位于学校的东北方向,
位于学校的东北方向, 位于学校南偏东
位于学校南偏东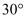 方向,
方向, 在
在 的南偏西
的南偏西 方向的
方向的 处.求学校
处.求学校 和红色文化基地
和红色文化基地 之间的距离.
之间的距离.
 和人工智能科技馆
和人工智能科技馆 参观学习.如图,学校在点
参观学习.如图,学校在点 处,
处, 位于学校的东北方向,
位于学校的东北方向, 位于学校南偏东
位于学校南偏东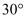 方向,
方向, 在
在 的南偏西
的南偏西 方向的
方向的 处.求学校
处.求学校 和红色文化基地
和红色文化基地 之间的距离.
之间的距离.
如图,在△ABC中,点D在边BC上,∠CAD=∠B,点E在边AB上,联结CE交AD于点H,点F在CE上,且满足CF•CE=CD•BC.

-
(1) 求证:△ACF∽△ECA;
-
(2) 当CE平分∠ACB时,求证:
 =
=  .
.
最近更新
- 如图所示,空间被分层若干个区域,分别以水平线aa'、bb'、cc'、dd'为界,每个区域的高度均为h,期中区域Ⅱ存在垂直
- (本题满分6分)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1.(1)证明:△A1A
- 在粒子对撞机中,有一个电子经过高压加速,速度达到光速的0.5倍,试求此时电子的质量变为静止时的多少倍?
- 十月社会主义革命首先发生在俄国的最重要客观条件是 ( ) A.俄国是帝国主义链
- 近日,中共中央印发了《中国党员领导干部廉洁从政著干准则》。准则规定,禁止违反规定干预和插手市场经济活动,谋取私利,禁止利
- 用相对分子质量为43的烷基取代甲苯苯环上的一个氢原子所得的芳香族产物数目( ) A.3种 B.4种
- 下图为某大陆北纬48°沿线地区的年降水量变化示意图。据此回答影响a地降水的主要风向是A.东南风 B.东
- 下列句子中,标点符号使用有错误的一项是 A.人的一生,总是在不停地尝试,尝试拥有,尝试放弃;人的一生,又始终在不断地追求
- D Beyond two or three days,the world’s best weather forecast
- 2015年,广东省依法赋予特大镇政府县级行政执法职责,依法委托一般镇、较大镇政府 和街道政府承担市场秩序监管执法职能,保
- 下图是绿色植物体内能量转换过程的示意图,请据图回答:(1)图中A表示的生理过程为___________,其中生成的AT
- (17分)(1)浓硫酸与木炭粉在加热条件下反应的化学方程式是: 。(2)试用下图所列各装置设计一个实验,来
- 下列句子的顺序排列正确的一项是( ) ①如果头脑里的语言材料很贫乏,总共就知道那么一点点,就会那么一点点,还说得上什
- 下图为患红绿色盲的某家族系谱图,该病为X染色体隐性遗传病,图中一定不带该致病基因的个体是A.1号
- 读日本和俄罗斯略图,完成小题。1.图中岛屿A是 ( )A.北海道 B.四国 C
- 对任意实数,圆C:与直线的位置关系是( ) A.相交 B.相切 C.相离
- 3、图中阴影所示广阔的平原地区人口稀疏的原因是:( ) A.气候干燥,荒漠广布 B.热量
- Sneaker is a kind of shoe worn by many people all over the w
- “太上,不知有之;其次,亲而誉之;其次,畏之;其次,侮之。……功成事遂,百姓皆谓:我‘自然’。”材料直接反映的主要政治
- A~H都是初中化学中的常见物质,它们之间的转化关系如图14所示。A是天然气的主要成分,E为固体,是一种常见的食品干燥剂。



