九年级(初三)数学下学期下册试题
已知圆锥的底面半径是2,母线长是4,则圆锥的侧面积是.
如图所示的几何体的主视图是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:  +2sin60°﹣3tan30°.
+2sin60°﹣3tan30°.
 +2sin60°﹣3tan30°.
+2sin60°﹣3tan30°.
已知y=y1﹣y2 , y1与x2成正比例,y2与x+3成反比例,当x=0时,y=2;当x=2时,y=0,求y与x的函数关系式,并指出自变量的取值范围.
如图是正方体的展开图,每个面都标注了字母,如果b在下面,c在左面,那么d在( )

A . 前面
B . 后面
C . 上面
D . 下面
在一间黑屋子里,用一盏白炽灯垂直向下照射一球状物,这个球状物体在地面的投影是形,当把球状物向下移动时,投影的大小变化应是.
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD , 在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米,试求该校地下停车场的限高CD(结果精确到0.1米,参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)

圆锥的展开图可能是下列图形中的( )
A .  B .
B .  C .
C .  D .
D . 
 C .
C .
如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“新”字一面的相对面上的字是( )

A . 代
B . 中
C . 国
D . 梦
-
(1) 计算:
 ;
;
-
(2) 若
 ,求
,求  的值.
的值.
如图,圆锥的母线长为2,底面圆的周长为3,则该圆锥的侧面积为( )

A . 3π
B . 3
C . 6π
D . 6
在一张比例尺为1:5000的地图上,艺术楼到学校食堂的图上距离为8cm,那么艺术楼到学校食堂的实际距离为m.
如图1,梯子斜靠在竖直的墙上,其示意图如图2,梯子与地面所成的角α为75° ,梯子AB长3m,求梯子顶部离地竖直高度BC.(结果精确到 0.1m;参考数据:sin75°≈0.97, cos75°≈0.26,tan75°≈3.73)


计算: 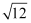 ﹣4
﹣4  ﹣tan60°+|
﹣tan60°+|  ﹣2|.
﹣2|.
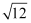 ﹣4
﹣4  ﹣tan60°+|
﹣tan60°+|  ﹣2|.
﹣2|.
如图1,矩形ABCD中,已知  ,
,  ,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将
,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将  沿直线AE翻折,点B的对应点为点
沿直线AE翻折,点B的对应点为点 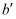 ,延长
,延长 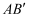 交CD于点M.
交CD于点M.
 ,
,  ,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将
,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将  沿直线AE翻折,点B的对应点为点
沿直线AE翻折,点B的对应点为点 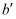 ,延长
,延长 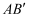 交CD于点M.
交CD于点M. 
-
(1) 求证:
 ;
;
-
(2) 如图2,若点
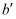 恰好落在对角线
恰好落在对角线  上,求
上,求  的值.
的值.
-
(1) 已知
 ,求
,求  的值;
的值;
-
(2) 已知直线
 分别截直线
分别截直线 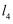 于点
于点  ,截直线
,截直线  于点
于点  ,且
,且  ,
,  ,求
,求  的长.
的长. 
在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为0.5,把△EFO缩小,则点E的对应点E′的坐标是( )
A . (﹣2,1)
B . (﹣8,4)
C . (﹣2,1)或(2,﹣1)
D . (﹣8,4)或(8,﹣4)
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为.

如图,点 在反比例函数
在反比例函数 的图象上,
的图象上, 轴于点M,点B是反比例函数
轴于点M,点B是反比例函数 的图象上一动点,过点
的图象上一动点,过点 作
作 轴于点N.
轴于点N.
 在反比例函数
在反比例函数 的图象上,
的图象上, 轴于点M,点B是反比例函数
轴于点M,点B是反比例函数 的图象上一动点,过点
的图象上一动点,过点 作
作 轴于点N.
轴于点N.
-
(1) 求反比例函数的解析式.
-
(2) 连接MN,BM.小华说:“当
 时,
时, 随着
随着 的增大而减小.”你同意小华的说法吗?请说明理由.
的增大而减小.”你同意小华的说法吗?请说明理由.
如图,在平行四边形  中,
中,  ,
,  ,
,  的面积为25,则四边形
的面积为25,则四边形  的面积为( )
的面积为( )
 中,
中,  ,
,  ,
,  的面积为25,则四边形
的面积为25,则四边形  的面积为( )
的面积为( ) 
A . 25
B . 9
C . 21
D . 16
最近更新
- 阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填
- 若右图所示阴影区为3月22日,空白区为3月21日,下列叙述正确的是A.太阳直射200S以南 B.太阳直射赤道或附近地点
- 符合东西走向,纬度最低的山脉是( ) A 天山 B 武夷山 C昆仑山
- 像油菜花儿一朵朵开 自大学毕业后一头扎入繁华都市,我每天都在睁大双眼寻找一切所谓的机遇——能迅速改变命运,让我的生活变得
- 多吃海带可预防“大脖子病”,这是因为海带中含有丰富的( )A.钾元素 B.碘元素 C.
- 根据句意,用所给的词组填空。how long howsoon how f
- 针对漫画《极刑》,我们应该( )(漫画说明:人类生产生活大量排放二氧化碳,导致全球变暖,危及人类生存。)①要停止对
- 完形填空(共20小题;每小题1分,满分20分) 阅读下面短文,掌握其大意,然后从下列各题所给的四个选项中,选出最佳选项。
- The new machine, if properly, will work forat least ten yea
- 古代中华儿女曾经创造出辉煌灿烂的中华文明。西欧有一名谚:“中国人的头,阿拉伯人的口,法兰西人的手。”结合古代科技史对此理
- 补写出下列名句名篇中的空缺部分。 ⑴念去去,千里烟波, 。 ⑵
- 如图10所示的电路中,电源电压不变,移动滑动变阻器R1的滑片P,当电流表的示数变化范围为1A~1.3A时,电压表的示数变
- 若为不等式组表示的平面区域,则当从-2连续变化到1时,动直线 扫过中的那部分区域的面积为 。
- 阅读下文,根据要求回答问题。 我生命中的那簇野菊花 赵宁 ①成长本是一个漫长的过程,历经岁月的不断锤炼打磨,才能由幼稚走
- 材料一:中国十七届四中全会审议通过了《中共中央关于加强和改进新形势下党 的建设若干重大问题的决定》,指出:世情、国情、党
- 已知函数,则的值是( ) A. B.4 C. D.
- 质点做匀速圆周运动,下列说法正确的是 A.速度越大,周期一定越小 B.角速度越大,周期一定越小 C.转速越大,
- (本题10分)如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,求这块地的面积。
- 质量为0.3kg的物体在水平面上运动,图中两直线分别表示物体受水平拉力和不受水平拉力时的速度-时间图像,则下列说法正确的
- “物以稀为贵”给企业生产者的启示有 ( ) ①务必重视产品的质量



