高中 数学
甲、乙、丙三位同学上课后独立完成5道自我检测题,甲及格的概率为  ,乙及格的概率为
,乙及格的概率为  ,丙及格的概率为
,丙及格的概率为  ,则三人至少有一个及格的概率为( )
,则三人至少有一个及格的概率为( )
 ,乙及格的概率为
,乙及格的概率为  ,丙及格的概率为
,丙及格的概率为  ,则三人至少有一个及格的概率为( )
,则三人至少有一个及格的概率为( )
A . 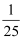 B .
B .  C .
C .  D .
D . 
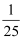 B .
B .  C .
C .  D .
D . 
下列四组函数中,表示同一函数的是( )
A . 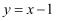 与
与  B .
B .  与
与  C .
C .  与
与  D .
D .  与
与 
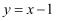 与
与  B .
B .  与
与  C .
C .  与
与  D .
D .  与
与 
已知函数  是R上的偶函数,其中e是自然对数的底数.
是R上的偶函数,其中e是自然对数的底数.
 是R上的偶函数,其中e是自然对数的底数.
是R上的偶函数,其中e是自然对数的底数.
-
(1) 求实数
 的值;
的值;
-
(2) 探究函数
 在
在  上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
-
(3) 若函数
 有零点,求实数m的取值范围.
有零点,求实数m的取值范围.
函数 的图象( )
的图象( )
 的图象( )
的图象( )
A . 关于原点对称
B . 关于 轴对称
C . 关于直线
轴对称
C . 关于直线 对称
D . 关于点
对称
D . 关于点 对称
对称
 轴对称
C . 关于直线
轴对称
C . 关于直线 对称
D . 关于点
对称
D . 关于点 对称
对称
根据下列情况,判断三角形解的情况,其中正确的是( )
A .  ,有两解
B .
,有两解
B .  ,有两解
C .
,有两解
C .  ,无解
D .
,无解
D .  ,有一解
,有一解
 ,有两解
B .
,有两解
B .  ,有两解
C .
,有两解
C .  ,无解
D .
,无解
D .  ,有一解
,有一解
直线l1:x+my+6=0与直线l2:(m﹣2)x+3y+2m=0互相平行,则m的值为.
袋子中装有若干个均匀的红球和白球,从中摸出一个红球的概率是  ,依次从中有放回地摸球,每次摸出一个,累计2次摸到红球即停止.记3次之内(含3次)摸到红球的次数为
,依次从中有放回地摸球,每次摸出一个,累计2次摸到红球即停止.记3次之内(含3次)摸到红球的次数为  ,则随机变量
,则随机变量  的数学期望
的数学期望  ( )
( )
 ,依次从中有放回地摸球,每次摸出一个,累计2次摸到红球即停止.记3次之内(含3次)摸到红球的次数为
,依次从中有放回地摸球,每次摸出一个,累计2次摸到红球即停止.记3次之内(含3次)摸到红球的次数为  ,则随机变量
,则随机变量  的数学期望
的数学期望  ( )
( )
A . 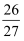 B .
B .  C .
C . 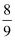 D .
D . 
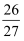 B .
B .  C .
C . 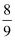 D .
D . 
已知  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C . 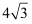 D .
D . 
 B .
B .  C .
C . 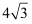 D .
D . 
已知45°<α<90°,函数f(x)=ax+b的图象如图,则函数g(x)=loga(x+b)的图象可能为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知点P是抛物线y2=4x上一点,设点P到此抛物线准线的距离为d1 , 到直线x﹣2y+4=0的距离为d2 , 则d1+d2的最小值是.
已知椭圆 :
: 的左、右焦点
的左、右焦点 ,
,  恰好是双曲线
恰好是双曲线 的左右顶点,椭圆
的左右顶点,椭圆 上的动点
上的动点 满足
满足 , 过点
, 过点 的直线
的直线 交椭圆C于
交椭圆C于 ,
,  两点.
两点.
 :
: 的左、右焦点
的左、右焦点 ,
,  恰好是双曲线
恰好是双曲线 的左右顶点,椭圆
的左右顶点,椭圆 上的动点
上的动点 满足
满足 , 过点
, 过点 的直线
的直线 交椭圆C于
交椭圆C于 ,
,  两点.
两点.
-
(1) 求椭圆
 的标准方程;
的标准方程;
-
(2) 椭圆
 上是否存在点
上是否存在点 使得四边形
使得四边形 (
( 为原点)为平行四边形?若存在,求出所有点
为原点)为平行四边形?若存在,求出所有点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
某企业生产某种电子设备的年固定成本为500(万元),每生产x台,需另投入成本  (万元),当年产量不足60台时,
(万元),当年产量不足60台时,  (万元);当年产量不小于60台时,
(万元);当年产量不小于60台时,  ,若每台售价为100(万元)时,该厂当年生产的该电子设备能全部销售完.
,若每台售价为100(万元)时,该厂当年生产的该电子设备能全部销售完.
 (万元),当年产量不足60台时,
(万元),当年产量不足60台时,  (万元);当年产量不小于60台时,
(万元);当年产量不小于60台时,  ,若每台售价为100(万元)时,该厂当年生产的该电子设备能全部销售完.
,若每台售价为100(万元)时,该厂当年生产的该电子设备能全部销售完.
-
(1) 写出年利润y(万元)关于年产量x(台)的函数关系式;
-
(2) 当年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?
平面直角坐标系  中,过点
中,过点  的直线
的直线  的参数方程为
的参数方程为  (
(  为参数);以原点
为参数);以原点  为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线  的极坐标方程为
的极坐标方程为  .
.
 中,过点
中,过点  的直线
的直线  的参数方程为
的参数方程为  (
(  为参数);以原点
为参数);以原点  为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线  的极坐标方程为
的极坐标方程为  .
.
-
(1) 求曲线
 的普通方程;
的普通方程;
-
(2) 若直线
 与曲线
与曲线  相交于
相交于  、
、  两点(点
两点(点  在
在  、
、  之间),且
之间),且  ,求
,求  的值.
的值.
已知函数 , 当
, 当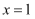 时,
时, 有极小值
有极小值 .
.
 , 当
, 当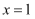 时,
时, 有极小值
有极小值 .
.
-
(1) 求
 的解析式;
的解析式;
-
(2) 设
 , 若对任意
, 若对任意 , 都有
, 都有
 成立,求实数
成立,求实数 的取值范围.
的取值范围.
用反证法证明命题:“已知x∈R,a=x2﹣1,b=2x+2,则a,b中至少有一个不小于0”,反设正确的是( )
A . 假设a,b都不大于0
B . 假设a,b至多有一个大于0
C . 假设a,b都大于0
D . 假设a,b都小于0
若复数 (其中i为虚数单位),则复数
(其中i为虚数单位),则复数 在复平面上对应的点位于( )
在复平面上对应的点位于( )
 (其中i为虚数单位),则复数
(其中i为虚数单位),则复数 在复平面上对应的点位于( )
在复平面上对应的点位于( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
某调查机构调查了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图(如图所示),则新生婴儿的体重(单位:kg)在[3.2,4.0)的人数是( )
A . 30;
B . 40;
C . 50;
D . 55.
已知椭圆的焦点为  ,
,  ,(
,(  ),
),  为椭圆上一点,且
为椭圆上一点,且  是
是  ,
,  的等差中项.
的等差中项.
 ,
,  ,(
,(  ),
),  为椭圆上一点,且
为椭圆上一点,且  是
是  ,
,  的等差中项.
的等差中项.
-
(1) 求椭圆方程;
-
(2) 如果点
 在第二象限且
在第二象限且  ,求
,求  的值.
的值.
求下列各式的值:
-
(1)

-
(2)

已知向量 与
与 的夹角为
的夹角为 ,
, ,则
,则 __________.
__________.
最近更新
- 第II卷(非选择题,共55分) 第三部分 写作(共三节,满分55分) 第一节 单词拼写(共10小题;每小题1分,满分10
- “观察DNA、RNA在细胞中分布”的实验中,下列正确的实验步骤是() A.水解→制片→冲洗→染色→观察
- 10.下图表示细胞分裂过程中染色体的形态变化,相关分析正确的是 A.甲→乙的过程中,染色质变成了染色体且细胞内染色体数
- 2016年3月18日山东济南非法经营疫苗系列案件发生后,党中央、国务院高度重视,责成有关部门和地方彻查涉案疫苗的流向和使
- 2.下列词语中,没有错别字的一项是( ) A.青睐 订书机 明火执杖 改弦更张 B.通牒 顶梁柱
- 人民群众是党的力量源泉和胜利之本,我们要坚持问政于民、问需于民、问计于民。从历史唯物主义角度看,“三问”表明中国 ①坚持
- 下列叙述中正确的是( ) ①标准状况下,1 L HCl和1 L H2O的物质的量相同 ②标准状况下,1 g H2和14
- 科学家用哺乳动物红细胞作材料来研究细胞膜的组成,是因为( ) A.哺乳动物红细胞容易得到 B.哺乳动物红细胞在水中
- 实验是化学研究的基础。对下列实验现象的描述错误的是 ① ② ③ ④ A.实验①烧杯中的澄清石灰水
- 2009年度诺贝生理学或医学奖由三位美国科学家伊丽莎白·布莱克本、卡罗尔·格雷德以及杰克·绍斯塔克共同获得,他们发现了由
- 某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:产品 每件售价(万元)
- 阅读下面的文字,完成后面题目。优雅的科学独行者卡迈什瓦尔·C·瓦利难以想象,如此优雅的美感,
- 一般来说,家庭农场是指以家庭成员为主要劳动力,利用从在农民手中采用出让、入股、租赁等方式流转来的土地,从事农业规模化、集
- 、激起欧洲人对东方的憧憬和向往的书籍是: A、《医学集成》 B、《徐霞客游记》 C、《医典》 D、《马可·波罗行记》
- 如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°
- From the cheers and shouts of _____, I gathered that he was
- 小明在做过滤操作时,在老师给他的仪器中,他认为还缺少一种,其中老师给的仪器主要有:漏斗、烧杯、滤纸、铁架台,那么他认为缺
- 细胞膜与其完成各种生理功能相适应,极为重要的结构特点( ) A.磷脂排列成双分子层 B
- (共5小题;每小题2分,满分10分) 根据短文内容,从下框的A---F选项中选出能概括每一段主题的最佳选项。 选项中有一
- Last Friday a storm swept through two villages in the New Te



