高中 数学
已知全集为  ,集合
,集合  ,
,  ,则
,则  ( )
( )
 ,集合
,集合  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  或
或  D .
D .  或
或 
 B .
B .  C .
C .  或
或  D .
D .  或
或 
tan300°=
已知一组鞋码与身高的数据(  表示鞋码,
表示鞋码,  表示身高),其中
表示身高),其中  .
.
 表示鞋码,
表示鞋码,  表示身高),其中
表示身高),其中  .
. | | 40 | 41 | 42 | 43 | 44 |
| | 172 | 175 | | | 183 |
若用此数据计算得到回归直线  ,则由此估计当鞋码为40时身高约为
,则由此估计当鞋码为40时身高约为  .
.
空间直角坐标系中,下列说法正确的是( )
A . 点  关于坐标平面
关于坐标平面  的对称点的坐标为
的对称点的坐标为  B . 点
B . 点  在平面
在平面  面上
C .
面上
C .  表示一个与坐标平面
表示一个与坐标平面  平行的平面
D .
平行的平面
D .  表示一条直线
表示一条直线
 关于坐标平面
关于坐标平面  的对称点的坐标为
的对称点的坐标为  B . 点
B . 点  在平面
在平面  面上
C .
面上
C .  表示一个与坐标平面
表示一个与坐标平面  平行的平面
D .
平行的平面
D .  表示一条直线
表示一条直线
用数学归纳法证明某命题时,左式为 +cosα+cos3α+…+cos(2n﹣1)α(α≠kπ,k∈Z,n∈N*)在验证n=1时,左边所得的代数式为( )
+cosα+cos3α+…+cos(2n﹣1)α(α≠kπ,k∈Z,n∈N*)在验证n=1时,左边所得的代数式为( )
 +cosα+cos3α+…+cos(2n﹣1)α(α≠kπ,k∈Z,n∈N*)在验证n=1时,左边所得的代数式为( )
+cosα+cos3α+…+cos(2n﹣1)α(α≠kπ,k∈Z,n∈N*)在验证n=1时,左边所得的代数式为( )
A .  B .
B .  +cosα
+cosα C .
C .  +cosα+cos3α
+cosα+cos3α D .
D .  +cosα+cos3α+cos5α
+cosα+cos3α+cos5α
 B .
B .  +cosα
+cosα C .
C .  +cosα+cos3α
+cosα+cos3α D .
D .  +cosα+cos3α+cos5α
+cosα+cos3α+cos5α
已知 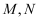 是不重合的直线,
是不重合的直线,  是不重合的平面,有下列命题:
是不重合的平面,有下列命题:
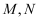 是不重合的直线,
是不重合的直线,  是不重合的平面,有下列命题:
是不重合的平面,有下列命题: ①若  ,则
,则  ;②若
;②若  ,则
,则  ;③若
;③若  ,则
,则  且
且  ;④若
;④若  ,则
,则  .
.
其中真命题的个数是( )
A . 0
B . 1
C . 2
D . 3
在等比数列{an}中,若a2=3,a5=24,则数列{an}的通项公式为( )
A .  •2n
B .
•2n
B .  •2n﹣2
C . 3•2n﹣2
D . 3•2n﹣1
•2n﹣2
C . 3•2n﹣2
D . 3•2n﹣1
 •2n
B .
•2n
B .  •2n﹣2
C . 3•2n﹣2
D . 3•2n﹣1
•2n﹣2
C . 3•2n﹣2
D . 3•2n﹣1
2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A . 茎叶图
B . 分层抽样
C . 独立性检验
D . 回归直线方程
如图,已知P是矩形ABCD所在平面外一点,PA⊥平面ABCD,E、F分别是AB,PC的中点.若∠PDA=45°,则EF与平面ABCD所成角的大小是( )

A . 90°
B . 60°
C . 45°
D . 30°
某程序框图如右图所示,该程序运行后输出的最后一个数是( )

A .  B .
B . 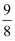 C .
C .  D .
D . 
 B .
B . 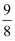 C .
C .  D .
D . 
复数  ,则
,则  的共轭复数是( )
的共轭复数是( )
 ,则
,则  的共轭复数是( )
的共轭复数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
对两个变量y和x进行回归分析,得到一组样本数据: ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
 ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A . 由样本数据得到的回归方程 必过样本中心
必过样本中心 B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数
B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的似合效果越好
D . 若变量y和x之间的相关系数为r=-0.9362,则变量y和x之间具有线性相关关系
越小,说明模型的似合效果越好
D . 若变量y和x之间的相关系数为r=-0.9362,则变量y和x之间具有线性相关关系
 必过样本中心
必过样本中心 B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数
B . 残差平方和越小的模型,拟合的效果越好
C . 用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的似合效果越好
D . 若变量y和x之间的相关系数为r=-0.9362,则变量y和x之间具有线性相关关系
越小,说明模型的似合效果越好
D . 若变量y和x之间的相关系数为r=-0.9362,则变量y和x之间具有线性相关关系
下列程序框图中,某班50名学生,在一次数学考试中, 表示学号为n的学生的成绩,则( )
表示学号为n的学生的成绩,则( )

A . P表示成绩不高于60分的人数
B . Q表示成绩低于80分的人数
C . R表示成绩高于80分的人数
D . Q表示成绩不低于60分,且低于80分人数
若一个等差数列 满足:①每项均为正整数;②首项与公差的积大于该数列的第二项且小于第三项,写出一个满足条件的数列的通项公式
满足:①每项均为正整数;②首项与公差的积大于该数列的第二项且小于第三项,写出一个满足条件的数列的通项公式 .
.
 满足:①每项均为正整数;②首项与公差的积大于该数列的第二项且小于第三项,写出一个满足条件的数列的通项公式
满足:①每项均为正整数;②首项与公差的积大于该数列的第二项且小于第三项,写出一个满足条件的数列的通项公式 .
.
射击运动中,一次射击最多能得10环,下图统计了某射击运动员50次射击命中环数不少于8环的频数,用频率估计概率,则该运动员在3次独立的射击中,总环数不少于28环的概率是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知全集 , 集合
, 集合 , 则
, 则 ( )
( )
 , 集合
, 集合 , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知m∈N*,则乘积m(m+1)(m+2)…(m+15)可表示为( )
A.A![]() B.A
B.A![]() C.A
C.A![]() D.A
D.A![]()
若![]() 并且
并且![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为![]()
![]() θ(弧度).
θ(弧度).
(1)求θ关于x的函数关系式;
 (2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
设等差数列![]() 的前n项和为Sn,且满足S2016>0,S2017<0,对任意正整数n,
的前n项和为Sn,且满足S2016>0,S2017<0,对任意正整数n,
都有![]() 则
则![]() 的值为( )
的值为( )
A.1006 B.1007 C.1008 D.1009
最近更新
- 下列措施不符合世博会“节能、环保、低碳”理念的是 A.“阳光谷”上采阳光、下蓄雨水,可给世博园区提供照明用电和生活用
- 如图,请你补充一个你认为正确的条件,使.∽:
- 有两个小灯泡,只标有额定电压,都是6.3伏。串联起来接到电源上,亮度不同。在回答哪个灯泡的额定功率比较大时,要用到以下6
- 验证空气中含有少量二氧化碳,将大针筒内的空气一次性压入新制的澄清石灰水,发现石灰水没有变化.据此,你认为该同学应该()A
- 18.补写下面名篇名句中的空缺部分。(6分) (1)悟以往之不谏,知来者之可追。 ,
- 在一个双链DNA分子中,碱基总数为m,腺嘌呤数为n,则下列有关结构数目正确的是( ) ①脱氧核苷酸数=磷酸数=碱基总
- 某同学为感受向心力的大小与那些因素有关,做了一个小实验:绳的一端拴一小球,手牵着在空中甩动,使小球在水平面内作圆周运动(
- We used to work in the same office and we _________ have cof
- 下列关于生态系统的叙述中,错误的是( ) A.生态系统的结构由生产者、消费者和分解者三种成分组成 B.生态系统中的能
- 赤道上没有气旋和反气旋的原因是( ) A.太阳辐射强 B.空气对流运动
- 已知cosα=,则sin(+α)=() A. B.﹣C.﹣D.
- 下列说法中不正确的是 A.家庭电路中的空气开关“跳闸”是发生短路造成的B.有人触电时,首先要采用的方法是切断电源 C.有
- A big step to strengthen China’s health care systems
- 读“世界某地区从M地至N地的地形剖面图”,回答1~2题。1.若M地正午太阳高度达一年中最小时,下列叙述正确的是 A.①地
- 在理论上,垂直自然带与相应水平自然带有下图所示对应关系。读图完成问题。从赤道向较高纬度地区,针叶林带在山地分布的海拔高度
- 如题(19)图,四棱锥P- ABCD中,PA⊥平面ABCD,AB∥CD,AB⊥AD,PA=CD=2AB=2,AD
- A、B、C、D、E为原子序数依次增大的五种短周期元素。E元素最高正价与最低负价的代数和为6,C单质既可与盐酸反应又可与N
- 下列叙述中哪些能表明基因与染色体的平行行为 A. DNA主要分布在染色体上,是染色体的主要化学组成之一 B.在细胞分
- 可用右图装置制取(必要时可加热)、净化、收集的气体是 A.
- 水果罐头盖上印有“如发现盖子鼓起,请勿选购”的字样,引起盖子鼓起的最可能原因是 A、好氧型细菌呼吸,产生CO2和H2O






