高中 数学
已知 M(2,-3),N(-3,-2),直线l经过点P(1,1),且与线段MN相交,则l的斜率k的取值范围是: ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列说法正确的是( )
A . 在(0,  )内,sinx>cosx
B . 函数y=2sin(x+
)内,sinx>cosx
B . 函数y=2sin(x+  )的图象的一条对称轴是x=
)的图象的一条对称轴是x= 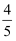 π
C . 函数y=
π
C . 函数y=  的最大值为π
D . 函数y=sin2x的图象可以由函数y=sin(2x﹣
的最大值为π
D . 函数y=sin2x的图象可以由函数y=sin(2x﹣  )的图象向右平移
)的图象向右平移  个单位得到
个单位得到
 )内,sinx>cosx
B . 函数y=2sin(x+
)内,sinx>cosx
B . 函数y=2sin(x+  )的图象的一条对称轴是x=
)的图象的一条对称轴是x= 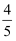 π
C . 函数y=
π
C . 函数y=  的最大值为π
D . 函数y=sin2x的图象可以由函数y=sin(2x﹣
的最大值为π
D . 函数y=sin2x的图象可以由函数y=sin(2x﹣  )的图象向右平移
)的图象向右平移  个单位得到
个单位得到
中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有个面,其棱长为.

已知复数z= (i是虚数单位),则z的实部是 .
(i是虚数单位),则z的实部是 .
 (i是虚数单位),则z的实部是 .
(i是虚数单位),则z的实部是 .
抛物线  的准线方程为( )
的准线方程为( )
 的准线方程为( )
的准线方程为( )
A .  B .
B .  C .
C . 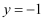 D .
D . 
 B .
B .  C .
C . 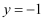 D .
D . 
在三角形  中,内角
中,内角  所对的边分别为
所对的边分别为  ,若
,若 
 ,则角
,则角  ( )
( )
 中,内角
中,内角  所对的边分别为
所对的边分别为  ,若
,若 
 ,则角
,则角  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
将圆锥侧面展开得到扇形AOB(图1),已知扇形AOB的半径和面积分别为2, , 现要探究在该扇形内截取一个矩形,应该如何截取,可以使得截取的矩形面积最大.现有两个实验小组,他们分别采用两种方案,方案一:如图2所示,将矩形的一边CD放在OA上,另外两个顶点E,F分别在弧AB和OB上;方案二:如图3所示,两个顶点D,E在弧AB上,另外两个顶点C,F分别在OA和OB上.
, 现要探究在该扇形内截取一个矩形,应该如何截取,可以使得截取的矩形面积最大.现有两个实验小组,他们分别采用两种方案,方案一:如图2所示,将矩形的一边CD放在OA上,另外两个顶点E,F分别在弧AB和OB上;方案二:如图3所示,两个顶点D,E在弧AB上,另外两个顶点C,F分别在OA和OB上.
 , 现要探究在该扇形内截取一个矩形,应该如何截取,可以使得截取的矩形面积最大.现有两个实验小组,他们分别采用两种方案,方案一:如图2所示,将矩形的一边CD放在OA上,另外两个顶点E,F分别在弧AB和OB上;方案二:如图3所示,两个顶点D,E在弧AB上,另外两个顶点C,F分别在OA和OB上.
, 现要探究在该扇形内截取一个矩形,应该如何截取,可以使得截取的矩形面积最大.现有两个实验小组,他们分别采用两种方案,方案一:如图2所示,将矩形的一边CD放在OA上,另外两个顶点E,F分别在弧AB和OB上;方案二:如图3所示,两个顶点D,E在弧AB上,另外两个顶点C,F分别在OA和OB上.
-
(1) 求圆锥的体积;
-
(2) 比较两种方案,哪种方案更优?并谈谈两种方案的区别与联系.
如图,在正三棱柱  中,
中,  为棱
为棱  的中点.
的中点.
 中,
中,  为棱
为棱  的中点.
的中点. 
-
(1) 证明:
 平面
平面  ;
;
-
(2) 证明:
 .
.
在  中,
中,  ,
,  ,
,  分别是内角
分别是内角  ,
,  ,
,  所对的边,
所对的边,  ,且
,且  ,
,  ,则以下说法正确的是( )
,则以下说法正确的是( )
 中,
中,  ,
,  ,
,  分别是内角
分别是内角  ,
,  ,
,  所对的边,
所对的边,  ,且
,且  ,
,  ,则以下说法正确的是( )
,则以下说法正确的是( )
A .  B . 若
B . 若  ,则
,则  C . 若
C . 若  ,则
,则  是等边三角形
D . 若
是等边三角形
D . 若  的面积是
的面积是  ,则该三角形外接圆半径为4
,则该三角形外接圆半径为4
 B . 若
B . 若  ,则
,则  C . 若
C . 若  ,则
,则  是等边三角形
D . 若
是等边三角形
D . 若  的面积是
的面积是  ,则该三角形外接圆半径为4
,则该三角形外接圆半径为4
若x=1满足不等式ax2+2x+1<0,则实数a的取值范围是( )
A . (﹣3,+∞)
B . (﹣∞,﹣3)
C . (1,+∞)
D . (﹣∞,1)
过点  且与直线
且与直线 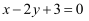 平行的直线方程是( )
平行的直线方程是( )
 且与直线
且与直线 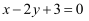 平行的直线方程是( )
平行的直线方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在等差数列{an}中,若a5+a8+a11=3,则该数列的前15项的和为
已知实数  满足
满足  ,则
,则  的最小值是( )
的最小值是( )
 满足
满足  ,则
,则  的最小值是( )
的最小值是( )
A . 4
B . 5
C . 6
D . 7
某几何体的正视图如图所示,这个几何体不可能是( )

A . 圆锥与圆柱的组合
B . 棱锥与棱柱的组合
C . 棱柱与棱柱的组合
D . 棱锥与棱锥的组合
若不等式 


.计算![]() -4cos10°=________.
-4cos10°=________.
在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]()
![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
已知集合![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
以双曲线![]() 的焦点为顶点,且渐近线互相垂直的双曲线的标准方程为( )
的焦点为顶点,且渐近线互相垂直的双曲线的标准方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
已知 中,
中, ,三角形
,三角形 的面积为
的面积为 ,且
,且 ,则
,则 ( )
( )
A. B. 3 C.
B. 3 C.  D. -
D. -
A.
最近更新
- “洹水安阳名不虚,三千年前是帝都。”安阳曾是下列哪一王朝的都城? A.商朝 B.东周
- 硫铁矿在高温下被氧气氧化并产生SO2气体:4FeS2+11O2→8SO2+2Fe2O3。设空气中N2占4/5、O2占1/
- 下列热化学方程式中ΔH的绝对值能表示可燃物的燃烧热的是A.H2(g)+Cl2(g)====2HCl(g);ΔH=-184
- 图10-10是两个农业生态系统的结构模式图。图10-10a是农作物为人类提供的食物量,为家禽和家畜提供的饲料,都与图10
- ---Could I borrow your dictionary?---Of course you ________.
- 下列为动物结构层次的是() A. 细胞→组织→器官→动物体 B. 细胞→组织→系统→动物体 C. 细胞→组织→器官→系统
- 定义在R上的函数f(x)满足f(x+2)=3f(x),当x∈[0,2]时,f(x)=x2-2x,则当x∈[-4,-2]时
- 目前撒哈拉以南非洲面临的主要问题为: A.干旱、能源和资源问题 B.人口、粮食和环境问题 C.人口、粮食和能源问题
- We had a very good v__________ of the whole island from wher
- 下列图片与戊戌政变后得以保留的新政措施关系最密切的是( )
- 对产生花粉植株的途径叙述,错误的是 A.花粉通过胚状体阶段发育成植株 B.花粉先形成愈伤组织再诱导分化成植株 C.花粉培
- 下列属于细胞膜的功能的是 A. 将细胞与外界环境分隔开 B.控制物质进出细胞 C. 进行细胞
- 阅读下列表格,回答有关问题:(8分) 材料一:“八五”末期,我国云南、贵州、四川三省贫困人口数量最多,总计2000万左右
- 下列各类物质中,一定含有氧元素的是 (A)单质
- 你知道用火柴竟可以点燃电灯泡的事吗?如图所示,用一段铅笔芯(石墨做的)接到电路上,使之成为滑动变阻器。当改变连入电路上
- 亚洲众多的河流呈放射状流向周边海洋,其影响因素是( ) A.亚洲气候 B.亚洲地势 C
- 将帅二三子夫妇以蕃 古义:____________ 今义:两三个孩子
- 糖元〔(C6H10O)n〕是一种相对分子质量比淀粉更大的多糖,主要存在于肝脏的肌肉中,所以又叫动物淀粉和肝糖。下列关于糖
- 某单位有三个科室,为实现减员增效,每科室抽调2人去参加再就业培训,培训后这6人中有2人返回原单位,但不回原科室工作,且每
- 在下列反应中,水既不作氧化剂,也不作还原剂的氧化还原反应是 A、Na2O2+H2O B、Na2O+H2O C



