高中 数学
已知平面向量  ,
,  ,
,  ,
,  ,
,  ,若向量
,若向量  满足
满足  ,则
,则  的最大值为.
的最大值为.
 ,
,  ,
,  ,
,  ,
,  ,若向量
,若向量  满足
满足  ,则
,则  的最大值为.
的最大值为.
一支车队有  辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午  时出发,第二辆车于下午
时出发,第二辆车于下午  时
时  分出发,第三辆车于下午
分出发,第三辆车于下午  时
时  分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午  时停下来休息.到下午
时停下来休息.到下午  时,最后一辆车行驶了多长时间?如果每辆车的行驶速度都是
时,最后一辆车行驶了多长时间?如果每辆车的行驶速度都是  ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少 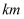 ?
?
 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午  时出发,第二辆车于下午
时出发,第二辆车于下午  时
时  分出发,第三辆车于下午
分出发,第三辆车于下午  时
时  分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午  时停下来休息.到下午
时停下来休息.到下午  时,最后一辆车行驶了多长时间?如果每辆车的行驶速度都是
时,最后一辆车行驶了多长时间?如果每辆车的行驶速度都是  ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少 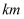 ?
?
设  且
且  则函数
则函数  与
与  在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
 且
且  则函数
则函数  与
与  在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则几何体的体积为( )
A . 6
B . 9
C . 12
D . 18
已知三个内角 所对的边分别为
所对的边分别为
 所对的边分别为
所对的边分别为
-
(1) 若
 , 求
, 求 的面积;
的面积;
-
(2) 设线段
 的中点为
的中点为 , 若
, 若 , 求
, 求 外接圆半径的值.
外接圆半径的值.
(极坐标与参数方程)在极坐标系中,曲线C1和C2的方程分别为ρsin2θ=cosθ和ρsinθ=1.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1和C2交点的直角坐标为.
已知O是坐标原点,F是双曲线 的右焦点,过双曲线C的右顶点且垂直于x轴的直线与双曲线C的一条渐近线交于A点,若以F为圆心的圆经过点A,O,则双曲线C的渐近线方程为( )
的右焦点,过双曲线C的右顶点且垂直于x轴的直线与双曲线C的一条渐近线交于A点,若以F为圆心的圆经过点A,O,则双曲线C的渐近线方程为( )
 的右焦点,过双曲线C的右顶点且垂直于x轴的直线与双曲线C的一条渐近线交于A点,若以F为圆心的圆经过点A,O,则双曲线C的渐近线方程为( )
的右焦点,过双曲线C的右顶点且垂直于x轴的直线与双曲线C的一条渐近线交于A点,若以F为圆心的圆经过点A,O,则双曲线C的渐近线方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知甲、乙两地的公路线长400千米,用10辆汽车从甲地向乙地运送一批物资,假设汽车以v千米/小时的速度直达乙地,为了某种需要,两汽车间距不得小于  千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是小时.
千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是小时.
 千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是小时.
千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是小时.
已知函数  ,若f(x)的最小值是a,则a=.
,若f(x)的最小值是a,则a=.
 ,若f(x)的最小值是a,则a=.
,若f(x)的最小值是a,则a=.
等差数列  中,
中,  ,
,  ,则
,则  ( )
( )
 中,
中,  ,
,  ,则
,则  ( )
( )
A . 14
B . 17
C . 20
D . 23
某品牌汽车  店对2020年该市前几个月的汽车成交量进行统计,用
店对2020年该市前几个月的汽车成交量进行统计,用  表示2020年第
表示2020年第  月份该店汽车成交量,得到统计表格如下:
月份该店汽车成交量,得到统计表格如下:
 店对2020年该市前几个月的汽车成交量进行统计,用
店对2020年该市前几个月的汽车成交量进行统计,用  表示2020年第
表示2020年第  月份该店汽车成交量,得到统计表格如下:
月份该店汽车成交量,得到统计表格如下: | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| | 14 | 12 | 20 | 20 | 22 | 24 | 30 | 26 |
参考数据及公式:  ,
,  ,
,  ,
,  .
.
-
(1) 求出
 关于
关于  的线性回归方程
的线性回归方程  ,并预测该店9月份的成交量;(
,并预测该店9月份的成交量;(  ,
,  精确到整数)
精确到整数)
-
(2) 该店为增加业绩,决定针对汽车成交客户开展抽奖活动,若抽中“一等奖”获5千元奖金;抽中“二等奖”获2千元奖金;抽中“祝您平安”则没有奖金.已知一次抽奖活动中获得“二等奖”的概率为
 ,没有获得奖金的概率为
,没有获得奖金的概率为  .现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额
.现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额  (千元)的分布列及数学期望.
(千元)的分布列及数学期望.
如图,已知椭圆 的离心率
的离心率 , 由椭圆
, 由椭圆 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为 .
.
 的离心率
的离心率 , 由椭圆
, 由椭圆 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为 .
. 
-
(1) 求椭圆
 的标准方程;
的标准方程;
-
(2) 设
 为椭圆
为椭圆 的右顶点,过点
的右顶点,过点 且斜率不为
且斜率不为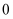 的直线
的直线 与椭圆
与椭圆 相交于点
相交于点 (点
(点 在
在 之间),若
之间),若 为线段
为线段 上的点,且满足
上的点,且满足 , 证明:
, 证明: .
.
已知函数  ,若
,若  ,则
,则  ( )
( )
 ,若
,若  ,则
,则  ( )
( )
A .  B .
B .  C .
C . 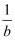 D .
D . 
 B .
B .  C .
C . 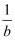 D .
D . 
中国的 技术领先世界,
技术领先世界, 技术的数学原理之一便是著名的香农公式:
技术的数学原理之一便是著名的香农公式: .它表示:在受噪音干扰的信道中,最大信息传递速度
.它表示:在受噪音干扰的信道中,最大信息传递速度 取决于信道带宽
取决于信道带宽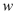 , 信道内信号的平均功率
, 信道内信号的平均功率 , 信道内部的高斯噪声功率
, 信道内部的高斯噪声功率 的大小,其中
的大小,其中 叫做信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,若带宽
叫做信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,若带宽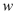 增大到原来的1.2倍,信噪比
增大到原来的1.2倍,信噪比 从1000提升到16000,则
从1000提升到16000,则 比原来大约增加了( )
比原来大约增加了( )
 技术领先世界,
技术领先世界, 技术的数学原理之一便是著名的香农公式:
技术的数学原理之一便是著名的香农公式: .它表示:在受噪音干扰的信道中,最大信息传递速度
.它表示:在受噪音干扰的信道中,最大信息传递速度 取决于信道带宽
取决于信道带宽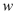 , 信道内信号的平均功率
, 信道内信号的平均功率 , 信道内部的高斯噪声功率
, 信道内部的高斯噪声功率 的大小,其中
的大小,其中 叫做信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,若带宽
叫做信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,若带宽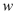 增大到原来的1.2倍,信噪比
增大到原来的1.2倍,信噪比 从1000提升到16000,则
从1000提升到16000,则 比原来大约增加了( )
比原来大约增加了( )(附: )
)
A . 32¥
B . 43%
C . 54%
D . 68%
某几何体的三视图如图所示,则该几何体的体积为( )

A.![]() B.4 C.2 D.
B.4 C.2 D.![]()
设长方体的长,宽,高分别为2a,a,a其顶点都在一个球面上,则该球的表面积为( )
A.3πa2 B.6πa2 C .12πa2 D.24πa2
几何证明选讲
如图,![]() 分别为
分别为![]() 边
边![]() 的中点,直线
的中点,直线![]() 交
交![]() 的外接圆于
的外接圆于![]() 两点,若
两点,若![]() ,证明:
,证明:
(1)![]() ;
;
(2)![]()

已知实数![]() ,
,![]() 满足
满足 ,则目标函数
,则目标函数![]() 的最小值为_____.
的最小值为_____.
为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据。
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)已知15位有意愿生二胎的女性公务员中有两位来自省妇联,该部门打算从这15位有意愿生二胎的女性公务员中随机邀请两位来参加座谈,设邀请的2人中来自省妇联的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

|
| 0.050 | 0.010 | 0.001 |
|
| 3.841 | 6.635 | 10.828 |
附:![]() ;
;
设集合![]() , B
, B![]() , 则
, 则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
最近更新
- 下列对银行的说法正确的是 A.我国的商业银行是我国金融体系中最重要的组成部分 B.贷款业务和存款业务分别是我国商业银行的
- 下列加点字的注音,完全正确的一项是( ) A.妖娆(ráo) 重荷(hé) 苦心孤诣(yì) B.绯(f
- 下列各句中,没有错别字的一项是 A.雷曼破产、美林被收购以及AIG面临的危机,使得全球金融市场再度风声鹤唳,一时间,世界
- 钴制是非常广泛的放射源,在医疗上常肺癌和肿瘤放射治疗。有关的说法中正确的是 A.质量数为27 B.质子数为
- 下列各句中,加点的成语使用最恰当的一句是 ( ) A.中国茶艺与日本茶道各有特点,但异曲同工,都强调“
- 对任意实数不等式恒成立,则实数的取值范围是( ) A. B. C. D.
- 某课题组研究激素类似物甲和乙对微型月季生根的影响,结果如下图所示。下列相关叙述中正确的是A.不含激素类似物甲和激素类似物
- There is a feeling in him that he'll be chosen to attend the
- 由磁感应强度的定义式B=F/IL可知 A、若某处的磁感应强度为零,则通电导线放在该处所受安培力一定为零 B、通电导线放在
- 类推的思维方法在化学学习与研究中常会产生错误的结论,因此类推的结论最终要经过实践的检验才能确定其正确与否。下列几种类推结
- 小明和小华用图甲所示的器材做“测定小灯泡的额定功率”的实验,小灯泡上标有“2.5V”的字样. (1) 将图甲中未连接部分
- 下列有关对1861年俄国农奴制改革的评述,不准确的一项是 A.改革具有资产阶级性质 B.扩大了自
- 在横线处填上合适的句子,使之与上下文形成句式整齐、语意连贯的一段话。 身心疲惫的时候,你可以告别课本,去感受旭日东升的朝
- 函数的单调递增区间是________.
- 如图,已知EF//BC,且AE∶BE=1∶2,若△AEF的面积为4,则△ABC的面积为________________.
- competence, you are quitesuited to the position, but y
- 如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边
- 2015年2月,科学家发现,一种名为“绿叶海天牛”的动物在摄取藻类后,能够将藻类的某一细胞结构置于自己的细胞内,从而使自
- 如图所示,为一质点作直线运动时的a~t图像,图中斜线部分的面积S表示( )A.速度 B.速度
- ________ is known to us all is _______ the 2008 Beijing Olym





