高中 数学
设函数  .
.
 .
.
-
(1) 若
 ,求
,求  的值;
的值;
-
(2) 若
 对
对  恒成立,求
恒成立,求  的取值范围.
的取值范围.
如果函数f(x)=  (a>0)在x=±1时有极值,极大值为4,极小值为0,试求函数f(x)的解析式.
(a>0)在x=±1时有极值,极大值为4,极小值为0,试求函数f(x)的解析式.
 (a>0)在x=±1时有极值,极大值为4,极小值为0,试求函数f(x)的解析式.
(a>0)在x=±1时有极值,极大值为4,极小值为0,试求函数f(x)的解析式.
下列不等式恒成立的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
以下说法正确的是。(填写所有正确命题的序号)
①不等式  与不等式
与不等式  解集相同;
解集相同;
②已知命题  “若
“若 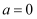 ,则
,则 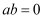 ”的否命题是“若
”的否命题是“若  ,则
,则  ” ,命题
” ,命题  “若
“若  ,则
,则  ”与命题“若
”与命题“若  ,则
,则  ”等价,则
”等价,则  为真命题,
为真命题,  为假命题;
为假命题;
③命题“  ”的否定是“
”的否定是“  ”;
”;
④已知幂函数  的图像经过点
的图像经过点  ,则
,则  。
。
四边形ABCD四顶点的坐标分别为A(0,0),B(1,0),C(2,1),D(0,3),将四边形绕y轴旋转一周得到一几何体,则此几何体的表面积为.
函数  的定义域是( )
的定义域是( )
 的定义域是( )
的定义域是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
不等式 的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A . {x|-1<x<3}
B . {x|x>3或x<-1}
C . {x|-3<x<1}
D . {x|x>1或x<-3}
已知不等式  的解集为
的解集为  ,若
,若  ,则实数
,则实数  的取值范围为.
的取值范围为.
 的解集为
的解集为  ,若
,若  ,则实数
,则实数  的取值范围为.
的取值范围为.
已知圆M的方程为x2+(y﹣2)2=1,直线l的方程为x﹣2y=0,点P在直线l上,过P点作圆M的切线PA,PB,切点为A,B.
-
(1) 若∠APB=60°,试求点P的坐标;
-
(2) 若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当
 时,求直线CD的方程;
时,求直线CD的方程;
-
(3) 求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标.
在四面体  中,
中,  ,则该四面体体积的最大值为.
,则该四面体体积的最大值为.
 中,
中,  ,则该四面体体积的最大值为.
,则该四面体体积的最大值为.
已知  ,求:
,求:
 ,求:
,求:
-
(1)
 及
及  ;
;
-
(2)
 ;
;
-
(3)
 .
.
若函数  的定义域是区间
的定义域是区间  ,则“
,则“  ”是“函数
”是“函数  在区间
在区间 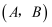 内存在零点”的( )
内存在零点”的( )
 的定义域是区间
的定义域是区间  ,则“
,则“  ”是“函数
”是“函数  在区间
在区间 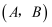 内存在零点”的( )
内存在零点”的( )
A . 充分而不必要条件
B . 必要而不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
将一个棱长为3cm的正方体铁块磨成一个球体零件,则可能制作的最大零件的体积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  的定义域为,单调递增区间为.
的定义域为,单调递增区间为.
 的定义域为,单调递增区间为.
的定义域为,单调递增区间为.
已知实数a,b,c,d成等比数列,且对函数y=ln(x+2)-x,当x=b时取到极大值c,则ad等于 ( )
A . -1
B . 0
C . 1
D . 2
已知 , 若集合
, 若集合 , 则“
, 则“ ”是“
”是“ ”的( )
”的( )
 , 若集合
, 若集合 , 则“
, 则“ ”是“
”是“ ”的( )
”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
经过  作直线
作直线  ,若直线
,若直线  与连接
与连接  的线段总有公共点,则直线
的线段总有公共点,则直线  的斜率的取值范围为.
的斜率的取值范围为.
 作直线
作直线  ,若直线
,若直线  与连接
与连接  的线段总有公共点,则直线
的线段总有公共点,则直线  的斜率的取值范围为.
的斜率的取值范围为.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
| PM2.5 日均值(微克/立方米) | |
| 2 | 8 5 |
| 3 | 2 1 4 3 |
| 4 | 4 5 |
| 6 | 3 8 |
| 7 | 9 |
| 8 | 6 3 |
| 9 | 2 5 |
(1)以这15天的PM2.5日均值来估计这360天的空气质量情况,则其中大约有多少天的空气质量达到一级.
(2)从这15天的数据中任取3天的数据,记X表示空气质量达到一级的天数,求X的分布列;
阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为 .

函数![]() 的值域为( )
的值域为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
最近更新
- 下列物质的水溶液不能使紫色石蕊试液变红的是( ) A. 稀硫酸 B. 氧化钙 C. 浓盐酸 D. 二氧化碳
- 下列句式不同类的一项是() A.度我至军中,公乃入 B.一鼓作气,再而衰,三而竭 C.戍卒叫,函谷举 D.夫秦王有虎狼之
- 保持氢气化学性质的粒子是( ) AH B H20 C H2 D 2H
- Sometimes we are asked _____ the likely result of an action
- 求证:ac+bd≤.
- 下表为《中华人民共和同居民身份证法》修改和通过的过程。2011年两会期间众多全国人大代表和政协委员针对第二代居民身份证使
- 有两个阻值相同的电阻,它们串联时的总电阻是并联时总电阻的________倍.
- (2015绵阳)有关人类的起源和发展,说法正确的是() A. 人类起源于现代类人猿 B. 人类的发展与环境的变化无关 C
- 若下图是城市内某一功能区不同时段的地铁使用量柱状图,则此区域最可能是A.工业区 B.中心商务区 C.低级住宅区 D
- So difficult _______it to work out the problem that I decide
- 若将各行星绕太阳的公转均视作匀速圆周运动,金星绕太阳运动半径小于地球绕太阳运动半径。则( )A.金星的公
- 在正三棱锥中,,,则此三棱锥的外接球的表面积为 .
- 补全下列名句名篇中的空缺部分。 ①山行六七里,渐闻水声潺潺而泻出于两峰之间者,酿泉也。______________ ,_
- 两次世界大战,给人类和平、发展和社会进步带来了重大影响。总结经验、制止战争、维护国际和平、建立平等国际关系、构建和谐世界
- 小红同学家的一台太阳能热水器安装在楼顶上,它可接收太阳能的真空镀膜管的总有效面积约为1. 5m2,可将接收的太阳能的40
- 目前,我国非公有制经济上缴国家的税收比重不断增加,95%中小企业是非公有制经济,私营企业和个体工商户从业人员共约1.5亿
- 如图所示,处于真空中的匀强电场与水平方向成15°角,在竖直平面内的直线AB与场强E互相垂直.在A点,以大小为v0的初速度
- 有机物分子中原子间(或原子与原子团间)的相互影响会导致物质化学性质的不同。下列各项的事实不能说明上述观点的是(
- 阅读下面的材料,根据要求写一篇不少于800字的文章。(60分) 从前,有一对仙人夫妻常在山顶下围棋。旁边有一棵树,树上住
- 元素观是化学的重要观念之一。下列有关元素的说法错误的是( ) A.物质都是由元素组成的 B.同



