高中 数学
某人造卫星在地球赤道平面绕地球飞行,甲、乙两个监测点分别位于赤道上东经131°和147°,在某时刻测得甲监测点到卫星的距离为1537.45 千米,乙监测点到卫星的距离为887.64 千米.假设地球赤道是一个半径为6378千米的圆,求此时卫星所在位置的高度(结果精确到0.01 千米)和经度(结果精确到0.01°).
方程  至少有一个负实根的充要条件是( )
至少有一个负实根的充要条件是( )
 至少有一个负实根的充要条件是( )
至少有一个负实根的充要条件是( )
A .  B .
B . 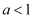 C .
C .  D .
D .  或
或 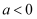
 B .
B . 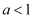 C .
C .  D .
D .  或
或 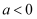
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟订的价格进行试销得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
-
(1) 求出y关于x的线性回归方程
 .其中
.其中  =250
=250
-
(2) 预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元每件,为使工厂获得最大利润,该产品的单价应定为多少元?
矩形ABCD中,  ,
, 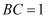 ,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
 ,
, 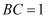 ,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知点M是边长为2的正方形ABCD的内切圆内(含边界)一动点,则  •
•  的取值范围是( )
的取值范围是( )
 •
•  的取值范围是( )
的取值范围是( )
A . [﹣1,0]
B . [﹣1,2]
C . [﹣1,3]
D . [﹣1,4]
-
(1) 已知
 ,求
,求  的解析式;
的解析式;
-
(2) 已知
 是定义在R上的奇函数,当
是定义在R上的奇函数,当  时,
时,  ,求当
,求当  时
时  的解析式.
的解析式.
函数  为定义在
为定义在  上的奇函数,则
上的奇函数,则  ,
,  .
.
 为定义在
为定义在  上的奇函数,则
上的奇函数,则  ,
,  .
.
在  中,“
中,“  ”是“
”是“  是钝角三角形”的( ).
是钝角三角形”的( ).
 中,“
中,“  ”是“
”是“  是钝角三角形”的( ).
是钝角三角形”的( ).
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
当  时,
时,  恒成立,则实数
恒成立,则实数  的取值范围( )
的取值范围( )
 时,
时,  恒成立,则实数
恒成立,则实数  的取值范围( )
的取值范围( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
二次曲线p= 的焦距为
的焦距为
 的焦距为
的焦距为
在 的展开式中x的系数为( )
的展开式中x的系数为( )
 的展开式中x的系数为( )
的展开式中x的系数为( )
A . 80
B . 240
C . -80
D . 160
某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( )

A . 20
B . 15
C . 10
D . 5
化简: 的值为( )
的值为( )
 的值为( )
的值为( )
A . 2+ B . 2-
B . 2- C . 1+
C . 1+ D .
D .  -1
-1
 B . 2-
B . 2- C . 1+
C . 1+ D .
D .  -1
-1
如图,在四棱锥  中,
中,  平面
平面  ,
,  ,
,  都是等腰直角三角形,
都是等腰直角三角形,  ,四边形
,四边形  是直角梯形,且
是直角梯形,且  ,
,  .
.
 中,
中,  平面
平面  ,
,  ,
,  都是等腰直角三角形,
都是等腰直角三角形,  ,四边形
,四边形  是直角梯形,且
是直角梯形,且  ,
,  .
. 
-
(1) 求证:
 ;
;
-
(2) 求点
 到平面
到平面  的距离.
的距离.
下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;④三角形内角和是
是奇函数;④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①② B. ①③④ C. ①②④ D. ②④
 如图,三定点
如图,三定点![]() 三动点D、E、M满足
三动点D、E、M满足
![]()
![]()
(I)求动直线DE斜率的变化范围;
(II)求动点M的轨迹方程。
先后连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角![]() 的概率是
的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线3x+y=0平行,若f(x)在区间上单调递减,则实数t的取值范围是__________.
如图,已知抛物线![]() 的焦点是
的焦点是![]() ,
,![]() ,
,
![]() 是抛物线
是抛物线![]() 上的两点,线段
上的两点,线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,若
,若
![]() .
.
(I)求点![]() 的坐标;
的坐标;  (II)求
(II)求![]() 面积的最大值.
面积的最大值.
 |
“ ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( )
A. 充要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
A. 充要条件 B. 充分而不必要条件
C. 必要而不充分条件 D. 既不充分也不必要条件
最近更新
- When you visit a museum you should the instructio
- Not until the wild wind calms down ___________(我们才出发)on our
- 按照前句形式,发挥想象仿写句子。 天空收容每一朵云彩,不论美丑,所以天空广阔无边; 大海收容每一粒水滴,不论清浊,所以大
- (6分)按照要求作图.(1)根据图甲中的入射光线画出相应的折射光线. (2)画出图乙中茶杯所受重力的示意图.(3)如图丙
- 据新华社2006年11月11日电,中国科学家发现细胞内小RNA分子具有基因激活功能,利用其激活肿瘤抑制基因,可以达到遏止
- 设周期为4的奇函数的定义域为,且当时,,则 的值为 .
- 双缝干涉实验中观察到的红光的干涉图样是 A.一系列明暗相间的同心圆
- 用数学归纳法证明:1-+-+…++…+(n∈N*),则从k到k+1时左边应添加的项为( )A.
- 将等体积的4×10-3mol·L-1的AgNO3溶液和4×10-3mol·L-1的K2CrO4溶液混合,是否能析出Ag2
- (2011•毕节地区)毕节地区水能资源丰富,理论蕴藏量达221.21万千瓦,己开发156万千瓦,把己开发水能资源用四舍五
- 下列句子中划线的近义词选用恰当的一项是( ) (1)有些人微笑不见得就 友善 (2)他很小就 出非凡的
- 20世纪第二个十年,以北大为主要中心,曾经大力宣传的思想是() ①兴民权、设议院 ②民主共和 ③民主和科学④提倡新文学,
- 下列对油污的处理方案中,对海洋环境影响最小的是 ( ) A.喷洒强效洗涤
- 用一根细线一端系一可视为质点的小球,另一端固定在一光滑锥顶上,如图(1)所示,设小球在水平面内作匀速圆周运动的角速度为ω
- 将一株质量为20g的黄瓜幼苗栽种在光照等适宜的环境中,一段时间后植株达到40g,其增加的质量来自于 A.水、矿质元素和空
- 已知集合M={x|ax2-1=0,x∈R}是集合N={y∈N*||y-1|≤1}的真子集,则实数a的取值个数是(
- (08年海拉尔二中阶段考试四文) 圆上到直线的距离等于的点有( )个. . .
- 当反应 COCl2(g) CO(g)+ Cl2(g) ; △H>0达到平衡时,下列措施:①升温 ②恒容通入惰性气体 ③增
- Tom ______ full marks, but he was too careless and made a sp
- 如图,有两个长度相同的滑梯靠在一面墙的两侧.已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的



