高中 数学
函数f(x)=| |的单调递增区间是( )
|的单调递增区间是( )
 |的单调递增区间是( )
|的单调递增区间是( )
A . (0, ]
B . (0,1]
C . (0,+∞)
D . [1,+∞)
]
B . (0,1]
C . (0,+∞)
D . [1,+∞)
 ]
B . (0,1]
C . (0,+∞)
D . [1,+∞)
]
B . (0,1]
C . (0,+∞)
D . [1,+∞)
有下列说法:
①梯形的四个顶点在同一个平面内;
②三条平行直线必共面;
③有三个公共点的两个平面必重合.
其中正确的个数是( )
A . 0
B . 1
C . 2
D . 3
如图,四棱锥S-ABCD中,底面是边长  为的正方形ABCD,AC与BD的交点为O,SO
为的正方形ABCD,AC与BD的交点为O,SO  平面ABCD且
平面ABCD且  ,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持  ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )
 为的正方形ABCD,AC与BD的交点为O,SO
为的正方形ABCD,AC与BD的交点为O,SO  平面ABCD且
平面ABCD且  ,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持  ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )

A . 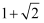 B .
B .  C .
C .  D .
D . 
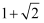 B .
B .  C .
C .  D .
D . 
如图,将一个大等边三角形分成三个全等三角形与中间的一个小等边三角形,设  .若在大等边三角形内任取一点P,则该点取自小等边三角形内的概率为( )
.若在大等边三角形内任取一点P,则该点取自小等边三角形内的概率为( )
 .若在大等边三角形内任取一点P,则该点取自小等边三角形内的概率为( )
.若在大等边三角形内任取一点P,则该点取自小等边三角形内的概率为( ) 
A . 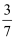 B .
B .  C .
C .  D .
D . 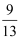
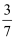 B .
B .  C .
C .  D .
D . 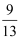
在 中,
中, ,
,  . 点
. 点 满足
满足 . 过点
. 过点 的直线
的直线 分别与边
分别与边 交于点
交于点 且
且 ,
,  . 已知点
. 已知点 为
为 的外心,
的外心, , 则
, 则 为.
为.
 中,
中, ,
,  . 点
. 点 满足
满足 . 过点
. 过点 的直线
的直线 分别与边
分别与边 交于点
交于点 且
且 ,
,  . 已知点
. 已知点 为
为 的外心,
的外心, , 则
, 则 为.
为.
在  中,
中,  ,
,  ,则
,则  的面积为( )
的面积为( )
 中,
中,  ,
,  ,则
,则  的面积为( )
的面积为( )
A .  B .
B .  C .
C .  D .
D . 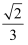
 B .
B .  C .
C .  D .
D . 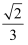
某公司有价值10万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,改造就需要投入,相应就要提高产品附加值,假设附加值  万元与技术改造投入
万元与技术改造投入  万元之间的关系满足:①
万元之间的关系满足:①  与
与  和
和  的乘积成正比;② 当
的乘积成正比;② 当  时,
时,  ;③
;③  ,其中
,其中  为常数,且
为常数,且  .
.
 万元与技术改造投入
万元与技术改造投入  万元之间的关系满足:①
万元之间的关系满足:①  与
与  和
和  的乘积成正比;② 当
的乘积成正比;② 当  时,
时,  ;③
;③  ,其中
,其中  为常数,且
为常数,且  .
.
-
(1) 设
 ,求出
,求出  的表达式,并求出
的表达式,并求出  的定义域;
的定义域;
-
(2) 求出附加值
 的最大值,并求出此时的技术改造投入的
的最大值,并求出此时的技术改造投入的  的值.
的值.
某校在某次学业水平测试后,随机抽取了若干份数学试卷,并对其得分(满分100分)进行统计,根据所得数据,绘制了如图所示的频率分布直方图(分组区间为 .根据试卷得分从低到高将学生的成绩分为
.根据试卷得分从低到高将学生的成绩分为 四个等级,每个等级中的学生人数占比如表所示.
四个等级,每个等级中的学生人数占比如表所示.
 .根据试卷得分从低到高将学生的成绩分为
.根据试卷得分从低到高将学生的成绩分为 四个等级,每个等级中的学生人数占比如表所示.
四个等级,每个等级中的学生人数占比如表所示.

|
成绩等级 |
|
|
|
|
|
得分范围 |
|
|
|
|
|
占比 |
20% |
30% |
30% |
20% |
-
(1) 求图中
 的值,并根据频率分布直方图估计该校学生这次学业水平测试数学成绩的平均分;(同一组中的数据用该组区间的中点值作代表)
的值,并根据频率分布直方图估计该校学生这次学业水平测试数学成绩的平均分;(同一组中的数据用该组区间的中点值作代表)
-
(2) 试确定成绩等级为B的得分范围(结果保留一位小数).
已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
-
(1) 求函数f(x)在[t,t+2](t>0)上的最小值;
-
(2) 对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
-
(3) 证明:对一切x∈(0,+∞),都有lnx>
 ﹣
﹣  成立.
成立.
从甲、乙等5名学生中随机选出2人,则甲被选中的概率为( )
A .  B .
B .  C .
C . 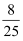 D .
D . 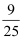
 B .
B .  C .
C . 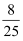 D .
D . 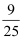
已知双曲线  的右焦点与抛物线
的右焦点与抛物线  的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
 的右焦点与抛物线
的右焦点与抛物线  的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
A .  B . 3
C . 5
D .
B . 3
C . 5
D . 
 B . 3
C . 5
D .
B . 3
C . 5
D . 
曲线 在点
在点 处的切线为.
处的切线为.
 在点
在点 处的切线为.
处的切线为.
已知非零向量 ,
,  满足
满足 , 则函数
, 则函数 是 ( )
是 ( )
 ,
,  满足
满足 , 则函数
, 则函数 是 ( )
是 ( )
A . 偶函数
B . 奇函数
C . 既是奇函数又是偶函数
D . 非奇非偶函数
已知全集  ,集合
,集合  ,
,  ,则
,则  ()
()
 ,集合
,集合  ,
,  ,则
,则  ()
()
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在复平面中,已知复数 对应的点在第二象限,则实数
对应的点在第二象限,则实数 的可能取值为( )
的可能取值为( )
 对应的点在第二象限,则实数
对应的点在第二象限,则实数 的可能取值为( )
的可能取值为( )
A . 0
B . 1
C . 2
D . 3
设函数  ,则( )
,则( )
 ,则( )
,则( )
A .  为
为  的极小值点
B .
的极小值点
B .  为
为  的极大值点
C .
的极大值点
C .  为
为  的极小值点
D .
的极小值点
D .  为
为  的极大值点
的极大值点
 为
为  的极小值点
B .
的极小值点
B .  为
为  的极大值点
C .
的极大值点
C .  为
为  的极小值点
D .
的极小值点
D .  为
为  的极大值点
的极大值点
若变量  ,
,  满足约束条件
满足约束条件  ,则
,则  的最大值是( )
的最大值是( )
 ,
,  满足约束条件
满足约束条件  ,则
,则  的最大值是( )
的最大值是( )
A .  B . 0
C . 5
D .
B . 0
C . 5
D . 
 B . 0
C . 5
D .
B . 0
C . 5
D . 
定义在R上的函数![]() 既是奇函数又是周期函数。若
既是奇函数又是周期函数。若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当
![]() 时,
时,![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B.![]() C.
C.![]() D.
D. ![]()
一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高,则自服药那一刻起,心率关于时间的一个可能的图象是( )
A. B.
B.
C. D.
D.
中心在原点,对称轴为坐标轴的双曲线 与圆
与圆 :
: 有公共点
有公共点 ,且圆
,且圆 在点
在点 处的切线与双曲线
处的切线与双曲线 的一条渐近线平行,则该双曲线的实轴长为________.
的一条渐近线平行,则该双曲线的实轴长为________.
最近更新
- 在图10所示的电路中,电源电压保持不变,电阻R1 的阻值为20欧。闭合电键S,电流表 A1 的示数为0.3安,电流表A2
- 下图中等高线图表示的地形名称依次是( ) A、山脊、盆地、山谷、山顶 B、山谷、山顶、山脊、盆地
- 阅读下面诗歌,按要求回答问题。(4分) 早 梅 唐·张渭 一树寒梅白玉条,迥临村路傍溪桥。 不知近水花
- 短文改错(共10小题;每小题1分,满分10分) 假定英语课上老师要求同桌之间交换修改作文,请你修改你同桌写的以下作文。文
- (14分)如图(甲)所示,在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A
- 单项选择 ,本题共有10个小题,请从每个小题的四个选项中,选出最佳答案。— Is AC MilanItalian foo
- (07年宣武区质检一理) 已知集合为
- 2009年12月,哥本哈根世界气候大会上强调汽车尾气已成为目前各国环境污染的重要源头之一,汽车尾气主要来自( ) A
- 洋务派主张“师夷长技以自强”,以下与洋务派这一主张不相符的一项是() A.工矿企业 B.新式学堂
- 下列物质分别与100 g 36.5%的盐酸恰好完全反应,反应后所得溶液中溶质的质量分数最小的是( ) A.M
- 学生使用的涂改液是一种使用频率极高的工具,涂改液中含有苯及其同系物,下列有关涂改液的说法不正确的是( ) A.苯的
- PS Camping is a company which started twenty five years ago.
- 如图12所示,空间分布着有理想边界的匀强电场和匀强磁场。左侧匀强电场的场强大小为E、方向水平向右,电场宽度为L;中间区域
- 依次填入横线上的词语最恰当的一项是( ) (2分) 在人类历
- 阅读下面这首小诗,按要求完成作文。(60分) 孩提时,我摔倒了/嚷着要大人抱起我 妈妈说,有人帮你是你的福运/自己起来才
- .一个正多边形的每个内角都等于150°,那么它是() A.正六边形 B.正八边形 C.正十边形 D.正十二边形
- 文言文阅读。(14分)吕蒙字子明,汝南富陂人也。少南渡,依姊夫邓当。当为孙策将,数讨山越。蒙年十五六,窃随当击贼,当顾见
- 近代中国对外战争多以失败告终,以历史发展趋势而言,其实质问题是( )A、战争性质决定战争成败
- 政治制度的创新是一个民族不断发展的动力,而政治民主是历史发展的必然趋势,古今中外人们都在不断地探索。阅读下列材料: 材料
- The factory produced many famous cars, none of ____ shipped










