高中 数学
已知复数  ,则其共轭复数
,则其共轭复数 =( )
=( )
 ,则其共轭复数
,则其共轭复数 =( )
=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若函数f(x)=2sin(2x+ )+a﹣1(a∈R)在区间[0,
)+a﹣1(a∈R)在区间[0, ]上有两个零点x1 , x2(x1≠x2),则x1+x2﹣a的取值范围是( )
]上有两个零点x1 , x2(x1≠x2),则x1+x2﹣a的取值范围是( )
 )+a﹣1(a∈R)在区间[0,
)+a﹣1(a∈R)在区间[0, ]上有两个零点x1 , x2(x1≠x2),则x1+x2﹣a的取值范围是( )
]上有两个零点x1 , x2(x1≠x2),则x1+x2﹣a的取值范围是( )
A . (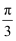 ﹣1,
﹣1,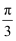 +1)
B . [
+1)
B . [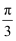 ,
, 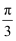 +1)
C . (
+1)
C . ( ﹣1,
﹣1, +1)
D . [
+1)
D . [ ,
,  +1)
+1)
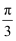 ﹣1,
﹣1,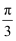 +1)
B . [
+1)
B . [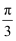 ,
, 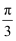 +1)
C . (
+1)
C . ( ﹣1,
﹣1, +1)
D . [
+1)
D . [ ,
,  +1)
+1)
如果  ,
,  ,
,  ,
,  的方差是
的方差是  ,则
,则  ,
,  ,
,  ,
,  的方差为( )。
的方差为( )。
 ,
,  ,
,  ,
,  的方差是
的方差是  ,则
,则  ,
,  ,
,  ,
,  的方差为( )。
的方差为( )。
A . 9
B . 3
C .  D . 6
D . 6
 D . 6
D . 6
某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另30人比较粗心.
-
(1) 试根据上述数据完成2×2列联表;
数学成绩及格
数学成绩不及格
合计
比较细心
比较粗心
合计
-
(2) 能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系.
参考数据:独立检验随机变量K2的临界值参考表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
 (其中n=a+b+c+d)
(其中n=a+b+c+d)
椭圆  的右焦点为
的右焦点为  ,其右准线与轴的交点为
,其右准线与轴的交点为  ,在椭圆上存在点
,在椭圆上存在点  满足线段
满足线段  的垂直平分线过点
的垂直平分线过点  ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )
 的右焦点为
的右焦点为  ,其右准线与轴的交点为
,其右准线与轴的交点为  ,在椭圆上存在点
,在椭圆上存在点  满足线段
满足线段  的垂直平分线过点
的垂直平分线过点  ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲、乙两种水稻.为了比较甲、乙两种水稻的产量,现从甲、乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:

附:  ;
;
| | 0.050 | 0.010 | 0.001 |
| | 3.841 | 6.635 | 10.828 |
-
(1) 根据茎叶图判断哪种水稻的产量更高?并说明理由;
-
(2) 求40株水稻颗粒重量的中位数
 ,并将重量超过
,并将重量超过  和不超过
和不超过  的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表: 超过

不超过

甲种水稻
乙种水稻
-
(3) 根据(2)中的列联表,能否有
 的把握认为两种水稻的产量有差异?
的把握认为两种水稻的产量有差异?
我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,记作数列  ,若数列
,若数列  的前
的前  项和为
项和为  ,则
,则  .
.
 ,若数列
,若数列  的前
的前  项和为
项和为  ,则
,则  .
. 
已知cos( ﹣α)=
﹣α)= cos(
cos( +β)=
+β)= sin(
sin( ﹣α)=-
﹣α)=- sin(
sin( +β),且0<α<π,0<β<π,求α,β的值.
+β),且0<α<π,0<β<π,求α,β的值.
 ﹣α)=
﹣α)= cos(
cos( +β)=
+β)= sin(
sin( ﹣α)=-
﹣α)=- sin(
sin( +β),且0<α<π,0<β<π,求α,β的值.
+β),且0<α<π,0<β<π,求α,β的值.
如图一个正方形花圃被分成5份.若给这5个部分种植花,要求相邻两部分种植不同颜色的花,已知现有红、黄、蓝、绿4种颜色不同的花,则不同的种植方法有种

如图,已知△ABC中,AB=  ,∠ABC=45°,∠ACB=60°.
,∠ABC=45°,∠ACB=60°.
 ,∠ABC=45°,∠ACB=60°.
,∠ABC=45°,∠ACB=60°. 
-
(1) 求AC的长;
-
(2) 若CD=5,求AD的长.
若直线l与直线3x+y+8=0垂直,则直线l的斜率为( )
A . ﹣3
B . ﹣  C . 3
D .
C . 3
D . 
 C . 3
D .
C . 3
D . 
将5名同学分到甲、乙、丙3个小组,若甲组至少两人,乙、丙组至少各一人,则不同的分配方案的种数为( )
A . 80
B . 120
C . 140
D . 50
若不等式 的解集是
的解集是 ,
,
 的解集是
的解集是 ,
,
-
(1) 求
 的值;
的值;
-
(2) 求不等式
 的解集;
的解集;
已知函数 .
.
 .
.
-
(1) 若
 , 求曲线
, 求曲线 在
在 处的切线方程;
处的切线方程;
-
(2) 若x=0为函数
 的极值点,且函数
的极值点,且函数 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)求![]() ;
;
(2)设函数![]() ,如果
,如果![]() 在开区间
在开区间![]() 上存在极小值,求实数
上存在极小值,求实数![]() 的取值范围.
的取值范围.
设原命题:若a+b≥2,则a,b中至少有一个不小于1,则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假
B.原命题假,逆命题真
C.原命题与逆命题均为真命题
D.原命题与逆命题均为假命题
![]() 依此类推,第
依此类推,第![]() 个等式为 .
个等式为 .
在![]() 中,已知
中,已知![]() ,
,![]() .
.![]() ,求
,求![]() ;
;
已知二次函数f(x)=ax2+bx+c,满足条件f(0)=0和f(x+2)-f(x)=4x.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数g(x)=f(x)-2mx+2,当x∈[1,+∞)时,求函数g(x)的最小值.
已知 ,设
,设 ,且
,且 ,记
,记 ;
;
(1)设 ,其中
,其中 ,试求
,试求 的单调区间;
的单调区间;
(2)试判断弦 的斜率
的斜率 与
与 的大小关系,并证明;
的大小关系,并证明;
(3)证明:当 时,
时, .
.
(1)设
(2)试判断弦
(3)证明:当
最近更新
- 2010年北京市节能工作的目标是:全市能源利用率由2004年的36.5%提高到40%;万元GDP能耗由2004年的1.2
- 肃乃辞孙权,至陆口,召吕蒙、甘宁商议,设宴于陆口寨外临江亭上,修下请书,选帐下能言快语一人为使,登舟渡江。江口关平问了,
- 阅读下面的漫画,按要求作文。 要求: ① 所写内容必须与画面内容相关 ②
- 为贯彻从紧的货币政策,中国人民银行决定:从 2007年 12月 21日起调整金融机构人民币存贷款基准利率,一年期存款基准
- 阅读下面两首唐诗,然后回答问题。(8分)渡湘江(杜审言)迟日园林悲昔游,今春花鸟作边愁。独怜京国人南窜①,不似湘江水北流
- 有关植物激素调节的说法,正确的是 A.生长素直接参与细胞代谢,从而调节植物生长 B.生长素浓度越高,促进植物生长的作用越
- 新时期,弘扬井冈山精神、长征精神、延安精神、红岩精神、西柏坡精神、抗震救灾精神,主要是因为() ①这些精神作为中国人的革
- 如图所示,mA=2mB,不计摩擦阻力,A物体自H高处由静止开始下落,且B物体始终在水平台面上.若以地面为零势能面,当物体
- 在20世纪30年代大危机的影响下发生的事件主要有( )①英国议会通过威斯敏斯特法 ②德国赔款问题不了了之③意大利法
- 经过30年的改革和发展,我国农业和农村经济的发展实现了历史性的跨越,中国人民终于摆脱了农产品长期短缺的困扰,圆了温饱梦。
- 小帆和小组的同学完成了下面的实验: (1)如图甲所示:(a)在探究“电流与电压关系”的实验中,滑动变阻器除保护电路外,还
- 下面短文中有10处语言错误。请在有错误的地方增加、删除或修改某个单词。 增加:在缺词处加一个漏字符号(∧), 并在其下面
- 如图所示,一个圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A点与水平地面AD相接,地面与圆心O等高,M
- 下列关于“一国两制”的叙述正确的是 ( ) ①《告台湾同胞书》最早提出这一伟大构思 ②是理论的重要组
- There used to be a coffee shop next to your house ,
- 下列说法中正确的是 A.C60气化和I2升华克服的作用力相同B.甲酸甲酯和乙酸的分子式相同,它们的熔点相近C.氯化钠和氯
- 在以下叙述中,可以将病毒与其他微生物相区别的是 ( ) A.能够使人或动、植物患病 B
- 下列性质的比较中,正确的是 A.氧化性:S > Cl2 B.金属性:K&
- 十七大报告指出:“要坚持中国特色社会主义政治发展道路,坚持党的领导、人民当家作主、依法治国有机统一,坚持和完善人民代表大
- 止痛药(阿托品)不损伤神经元的结构,在阻断神经冲动传导过程中,检测到突触间隙中神经递质的量不变。试推测它的作用机制是 A





