高中 数学
若  ,则不等式
,则不等式  的解集是( )
的解集是( )
 ,则不等式
,则不等式  的解集是( )
的解集是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设离散型随机变量ξ的概率分布如下:则表中的a的值为( )
ξ | 1 | 2 | 3 | 4 |
P | | | | a |
A . 1
B .  C .
C . 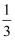 D .
D . 
 C .
C . 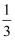 D .
D . 
若排列数  =6×5×4,则m=.
=6×5×4,则m=.
 =6×5×4,则m=.
=6×5×4,则m=.
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,分别记录如下:
甲:52,51,49,48,53,48,49;
乙:60,65,40,35,25,65,60.
-
(1) 这种抽样方法是哪一种抽样方法?
-
(2) 画出茎叶图,并说明哪个车间的产品比较稳定。
若函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则 的取值是( )
的取值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如果等差数列 中,
中, , 那么
, 那么 等于( )
等于( )
 中,
中, , 那么
, 那么 等于( )
等于( )
A . 21
B . 30
C . 35
D . 40
已知复数 (
( 为虚数单位),则
为虚数单位),则 为( )
为( )
 (
( 为虚数单位),则
为虚数单位),则 为( )
为( )
A . 1
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
设  ,则“
,则“  ”是“
”是“  ”的( )
”的( )
 ,则“
,则“  ”是“
”是“  ”的( )
”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分又不必要条件
函数  是定义在
是定义在  上的奇函数,
上的奇函数,  时
时  ,则不等式
,则不等式  的解集是( )
的解集是( )
 是定义在
是定义在  上的奇函数,
上的奇函数,  时
时  ,则不等式
,则不等式  的解集是( )
的解集是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
给出下列演绎推理:“自然数是整数, ▲ , 所以2是整数”,如果这是推理是正确的,则其中横线部分应填写.
一个几何体的三视图如右图所示,则该几何体的体积为( )
A . 16
B . 12
C . 8
D . 4
若(1+x)n=1+a1x+a2x2+a3x3+…+xn(n∈N*),且a1:a3=1:2,则n=.
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C1的方程为ρsin(θ+ 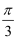 )+2
)+2  =0,曲线C2的参数方程为
=0,曲线C2的参数方程为  (θ为参数).
(θ为参数).
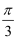 )+2
)+2  =0,曲线C2的参数方程为
=0,曲线C2的参数方程为  (θ为参数).
(θ为参数).
-
(1) 将C1的方程化为直角坐标方程;
-
(2) 若点Q为C2上的动点,P为C1上的动点,求|PQ|的最小值.
如果A为锐角, =-
=- ,那么cos
,那么cos =( )
=( )
 =-
=- ,那么cos
,那么cos =( )
=( )
A .  B . -
B . - C .
C .  D . -
D . -
 B . -
B . - C .
C .  D . -
D . -
已知函数  ,函数
,函数  有4个零点,则实数
有4个零点,则实数  的取值范围是( )
的取值范围是( )
 ,函数
,函数  有4个零点,则实数
有4个零点,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
检测新型冠状病毒特异序列的方法最常见的是荧光定量PCR(聚合酶链式反应).在PCR反应体系中,如反应体系存在靶序列,PCR反应时探针与模板结合,DNA聚合酶沿模板利用酶的外切酶活性将探针酶切降解,报告基团与淬灭基团分离,发出荧光.荧光定量PCR仪是病毒检测过程中的核心设备,能够监测出荧光到达预先设定阈值的循环数(Ct值)与病毒核酸浓度有关,病毒核酸浓度越高,Ct值越小.某第三方核酸检测机构先后采用过甲、乙两家公司的荧光定量PCR仪,日核酸检测量分别为600管和1000管,现两家公司分别推出升级方案,受各种因素影响,升级后核酸检测量变化情况与相应概率p如下表所示:
甲公司:
日核酸检测量 | 增加200% | 增加50% | 降低10% |
p |
|
|
|
乙公司:
日核酸检测量 | 增加80% | 增加50% | 增加10% |
p |
|
|
|
-
(1) 求至少有一家公司的升级方案使得日核酸检测量增加不低于50%的概率;
-
(2) 以日核酸检测量为依据,该检测机构应选哪家公司的仪器?
设函数f(x)=|x+1|+|x-a|(a>0).若不等式f(x)≥5的解集为(-∞,-2]∪(3,+∞),则a的值为________.
用秦九韶算法求n次多项式f(x)=![]() ,当x=
,当x=![]() 时,求
时,求![]() 需要算乘方、乘法、加法的次数分别为( )
需要算乘方、乘法、加法的次数分别为( )
A、![]() B、 n,
B、 n,![]() ,n C、0,
,n C、0,![]() ,n D、 0,n,n
,n D、 0,n,n
已知![]() 的定义域为
的定义域为![]() ,
,![]() 的导函数,且满足
的导函数,且满足![]() ,则不等式
,则不等式![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]() C.(1,2) D.
C.(1,2) D.![]()
曲线![]() 在点
在点![]() 处的切线倾斜角为( )
处的切线倾斜角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 关于美国1787年宪法的评价,不正确的是( ) A.是一部具有资产阶级性质的宪法 B.对美国资产阶级政权的巩固具有重大的
- 上海世博会专门设立了1亿美元专项资金用于发展中国家参展,目前有120个中低收入的发展中国家受益。242个国家和国际组织汇
- 解决我国水资源短缺问题的根本出路是( )A .兴建水库B .提高水价C .跨流域调水D .节约、保护水资源
- 某地水平运动物体向左偏,一年中只有一天有太阳直射,该地位于 A.北回归线 B.南回归线 C.
- 七年级3班小奇同学进行研究性学习,他搜集了“贞观之治”、“开元盛世”、“玄奘西游”、“鉴真东渡”的相关资料,由此推断他研
- .根据如图所示的实验装置图,回答问题:(1)写出图中仪器①的名称:________ (2)实验室制取二氧化碳气体,
- 人类镰刀型细胞贫血症发生的根本原因是() A.基因突变 B.基因重组 C.染色体结构变异 D.染色体数目变异
- 下列关于哺乳动物胚胎发育和胚胎工程的叙述,错误的是 () A.利用胚胎分割技术可以获得两个或多个基因型相同的胚胎
- 去括号后等于的是A. B. C. D.
- 阅读下面一首唐诗,回答问题。(8分)渡桑乾刘皂客舍并州已十霜,归心日夜忆咸阳。无端更渡桑乾水,却望并州是故乡。(1)结合
- 根据表中的已知条件,判断苏氨酸的密码子是 A.TGU B.UGA C.ACU D.UCU
- [物理——选修3-4] (1)一列简谐横波以10m/s的速度沿x轴正方向传播,t = 0时刻这列波的波形如图所示。则a质
- 下列属于生物多样性间接价值的是
- 下图是我国长江中下游某省地图,读后回答:(1)判断M地区的农业地域类型,并分析其发展农业有利的自然区位条件。 (2)该省
- 10、都江堰水利工程的主要组成部分是 ①二王庙 ②分水鱼嘴 ③石人水尺 ④飞
- 近年来,网络反腐蔚然成风,各级纪委对此也做出了积极回应,一大批问题官员迅速落马,网络举报成为公众参与反腐败的重要途径。这
- Thanks to the most advanced medical technology, the patient
- As we all know, an island is a piece of land ________ by wat
- It was not until midnight __ they reached the camp site.A .t
- 任务型阅读从A、B、C、D、E、F六个选项中选择正确的选项作为文章第3-7段小标题,并将序号填入第1-5五个空格中,其中








