高中 数学
已知复数z满足  ,则复数
,则复数  的模为.
的模为.
 ,则复数
,则复数  的模为.
的模为.
如图,抛物线  :
:  的焦点为
的焦点为  ,过点
,过点  的直线
的直线  与抛物线
与抛物线  交于
交于  ,
,  两点,若直线
两点,若直线  与以
与以  为圆心,线段
为圆心,线段  (
(  为坐标原点)长为半径的圆交于
为坐标原点)长为半径的圆交于  ,
,  两点,则关于
两点,则关于  值的说法正确的是( )
值的说法正确的是( )
 :
:  的焦点为
的焦点为  ,过点
,过点  的直线
的直线  与抛物线
与抛物线  交于
交于  ,
,  两点,若直线
两点,若直线  与以
与以  为圆心,线段
为圆心,线段  (
(  为坐标原点)长为半径的圆交于
为坐标原点)长为半径的圆交于  ,
,  两点,则关于
两点,则关于  值的说法正确的是( )
值的说法正确的是( ) 
A . 等于4
B . 大于4
C . 小于4
D . 不确定
奇函数f(x)的定义域为(﹣1,1),且在(﹣1,1)上是增函数,若f(1﹣a)+f(1﹣2a)<0,求实数a的取值范围.
7人排成一排,若A、B两人连排在一起,C、D、E三人两两不相邻,F、G两人顺序一定,不同的排法有种?
将数字“124467”重新排列后得到不同的偶数个数为( )
A . 72
B . 120
C . 192
D . 240
如图,一矩形  的一边
的一边  在
在  轴上,另两个顶点
轴上,另两个顶点  、
、  在函数
在函数  ,
,  的图像上,则此矩形绕
的图像上,则此矩形绕  轴旋转而成的几何体的体积的最大值是
轴旋转而成的几何体的体积的最大值是
 的一边
的一边  在
在  轴上,另两个顶点
轴上,另两个顶点  、
、  在函数
在函数  ,
,  的图像上,则此矩形绕
的图像上,则此矩形绕  轴旋转而成的几何体的体积的最大值是
轴旋转而成的几何体的体积的最大值是 
定义在 上的奇函数
上的奇函数 在
在 上是减函数,若
上是减函数,若 , 则实数
, 则实数 的取值范围为.
的取值范围为.
 上的奇函数
上的奇函数 在
在 上是减函数,若
上是减函数,若 , 则实数
, 则实数 的取值范围为.
的取值范围为.
已知函数  为偶函数.
为偶函数.
 为偶函数.
为偶函数.
-
(1) 求实数
 的值;
的值;
-
(2) 记集合
 ,
,  ,判断
,判断  与
与  的关系;
的关系;
-
(3) 当
 时,若函数
时,若函数  的值域为
的值域为  ,求
,求 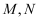 的值.
的值.
曲线  在点
在点  处的切线方程与坐标轴围成的三角形面积为.
处的切线方程与坐标轴围成的三角形面积为.
 在点
在点  处的切线方程与坐标轴围成的三角形面积为.
处的切线方程与坐标轴围成的三角形面积为.
某兴趣小组有男生20人,女生10人,从中抽取一个容量为5的样本,恰好抽到2名男生和3名女生,则①该抽样可能是系统抽样;②该抽样可能是随机抽样:③该抽样一定不是分层抽样;④本次抽样中每个人被抽到的概率都是  .其中说法正确的为( )
.其中说法正确的为( )
 .其中说法正确的为( )
.其中说法正确的为( )
A . ①②③
B . ②③
C . ②③④
D . ③④
已知△ABC中.
-
(1) 设
 •
•  =
=  •
•  ,求证:△ABC是等腰三角形;
,求证:△ABC是等腰三角形;
-
(2) 设向量
 =(2sinC,﹣
=(2sinC,﹣  ),
),  =(sin2C,2cos2
=(sin2C,2cos2  ﹣1),且
﹣1),且  ∥
∥  ,若sinA=
,若sinA= 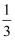 ,求sin(
,求sin( 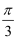 ﹣B)的值.
﹣B)的值.
已知函数f(x)=loga(ax﹣1)(a>0,且a≠1).
-
(1) 求函数f(x)的定义域;
-
(2) 若函数f(x)的函数值大于1,求x的取值范围.
设函数  ,当a=1时,f(x)的最小值是;若
,当a=1时,f(x)的最小值是;若  恒成立,则a的取值范围是.
恒成立,则a的取值范围是.
 ,当a=1时,f(x)的最小值是;若
,当a=1时,f(x)的最小值是;若  恒成立,则a的取值范围是.
恒成立,则a的取值范围是.
在如右上图的程序图中,输出结果是( )
A . 5
B . 10
C . 20
D . 15
对于函数  ,若存在区间
,若存在区间  ,当
,当  时的值域为
时的值域为  ,则称
,则称  为
为  倍值函数.若
倍值函数.若  是
是  倍值函数,则实数
倍值函数,则实数  的取值范围是( )
的取值范围是( )
 ,若存在区间
,若存在区间  ,当
,当  时的值域为
时的值域为  ,则称
,则称  为
为  倍值函数.若
倍值函数.若  是
是  倍值函数,则实数
倍值函数,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,为了计算衡水湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C之间的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据:![]() =1.414,
=1.414,![]() =1.732,
=1.732,![]() =2.236).
=2.236).

若直线经过A (2![]() , 9)、B(4
, 9)、B(4![]() , 15)两点, 则直线A B的斜率是( )
, 15)两点, 则直线A B的斜率是( )
![]()
![]()
![]()
![]()
设集合![]() ,函数
,函数![]()
![]()

![]() 且
且![]() 则
则![]() 的取值范围是
的取值范围是
A.(![]() ] B.(
] B.(![]() ] C.(
] C.(![]() ) D.[0,
) D.[0,![]() ]
]
正实数x,y满足xy+x+2y=6,则xy的最大值为 ,x+y的最小值为 .
已知在 中,
中, ,
, ,
, ,
, 为
为 内一点,
内一点, ,则
,则 的最小值为__________.
的最小值为__________.
最近更新
- 已知□ABCD,对角线AC,BD相交于点O,请你添加一个适当的条件,使□ABCD成为一个菱形.你添加的条件是
- 政治自由是民主政治的基础,是人民行使当家作主权利的重要方式,是社会主义民主的具体体现,但公民在行使政治自由时 A 必须正
- 下图是光合作用过程的图解,请对图仔细分析后回答下列问题: (1)H是
- -Although she sometimes loses her temper, her students like
- 阅读《假想金箍棒》,按要求完成18~22题(16分) ①《西游记》中孙悟空从东海龙王那里借了一根“定海神针”,又称“如意
- 根据中国人民银行公布的外汇牌价,2009年1月10日100美元可兑人民币690.91元,2009年10月10日100美元
- 下列仪器常用于物质分离的是()A.②③ B.①④ C.②④ D.①②
- 补写出下列名篇名句中的空缺部分。 (1)半卷红旗临易水, 。报君黄金台上意, 。 (
- 按要求修改下面的观察日记。 ×月×日 星期三 小雨转多云 今天早晨,我在小区运动场玩,①忽然看到双杠上挂着一幅蜘蛛网。②
- 我们今天所使用的农历,来源于( ) A.夏朝 B.商朝 C.西周 D
- 用如图甲所示的电路可以测量一个未知电阻的阻值,其中Rx为待测电阻,R为电阻箱 ,s为单刀双掷开关,R。为定值电阻.某同
- 下列归纳或类推中,正确的是( ) A.将HCl和SO2分别通入石蕊试液中,溶液都变为红色,所以它们都是酸类物质 B
- 将一支点燃的蜡烛放在一个凸透镜前某个位置,在凸透镜另一侧的光屏上得到了清晰放大的像,那么蜡烛位于此凸透镜的 A.焦距
- 关于日本的工业,正确的是( ) A.世界工业小国 B.临海型工业布局 C.原料自给,成品自销 D.大力发展消耗原料多
- 在我国现阶段,包括工人、农民、知识分子、干部、解放军指战员和其他社会主义劳动者、社会主义事业建设者、拥护社会主义的爱国者
- 在庆祝中国成立85周年大会上的讲话中指出,中国人民正是在长期的历史比较中,考虑选择我们党作为自己根本利益的代表,作为国家
- 某公司的会议成本计算方法是:会议成本=每小时平均工资的3倍×2×开会人数×会议时间(小时)。公式中平均工资之所以乘以3,
- (本小题满分7分)(1)(3分)计算: (2)(4分)已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD
- The storm left, _________ a lot of damage to this area. A. c
- 经济的发展,折射出时代的变迁,影响着社会的进程。阅读下列材料,回答问题。 材料一朝代 粮食亩产水平(市斤) 人均粮食占有



