高中 数学
已知函数  .
.
 .
.
-
(1) 若
 在
在  为增函数,求实数
为增函数,求实数  的取值范围;
的取值范围;
-
(2) 当
 时,函数
时,函数  在
在  的最小值为
的最小值为  ,求
,求  的值域.
的值域.
在  中,已知
中,已知  ,
,  ,
,  为
为  上一点,且
上一点,且  ,
,  为边
为边  的中点,且
的中点,且  ,则该三角形外接圆的半径为.
,则该三角形外接圆的半径为.
 中,已知
中,已知  ,
,  ,
,  为
为  上一点,且
上一点,且  ,
,  为边
为边  的中点,且
的中点,且  ,则该三角形外接圆的半径为.
,则该三角形外接圆的半径为.
若等边三角形一边所在直线的斜率为  ,则该三角形另两条边所在直线斜率为( )
,则该三角形另两条边所在直线斜率为( )
 ,则该三角形另两条边所在直线斜率为( )
,则该三角形另两条边所在直线斜率为( )
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 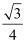
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 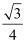
已知函数  的定义域为
的定义域为  .
.
 的定义域为
的定义域为  .
.
-
(1) 求函数
 的定义域
的定义域  ;
;
-
(2) 当
 时,求函数
时,求函数  的值域.
的值域.
已知  ,则f(1)+f(2)+f(3)+…+f(2017)=( )
,则f(1)+f(2)+f(3)+…+f(2017)=( )
 ,则f(1)+f(2)+f(3)+…+f(2017)=( )
,则f(1)+f(2)+f(3)+…+f(2017)=( )
A . 2017
B . 1
C .  D .
D . 
 D .
D . 
已知函数f(x)=log3(x2+ax+a+5),f(x)在区间(﹣∞,1)上是递减函数,则实数a的取值范围为:
.
tan  =( )
=( )
 =( )
=( )
A . ﹣  B . ﹣
B . ﹣  C .
C .  D .
D . 
 B . ﹣
B . ﹣  C .
C .  D .
D . 
三角形  中,
中,  ,
,  ,则
,则  ( )
( )
 中,
中,  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,边BC=2,AB= , 则角C的取值范围是 .
, 则角C的取值范围是 .
 , 则角C的取值范围是 .
, 则角C的取值范围是 .
已知集合A={x|x3+2x2﹣x﹣2>0},B={x|x2+ax+b≤0},且A∪B={x|x+2>0},且A∩B={x|1<x≤3},那么a+b=.
下列命题为真命题的是( )
A . 若 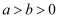 ,则
,则 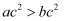 B . 若
B . 若  ,则
,则  C . 若
C . 若 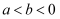 ,则
,则  D . 若
D . 若 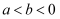 ,则
,则 
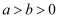 ,则
,则 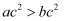 B . 若
B . 若  ,则
,则  C . 若
C . 若 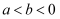 ,则
,则  D . 若
D . 若 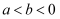 ,则
,则 
解关于x的不等式 

函数 在
在 上为单调函数,则实数a的取值范围可以是( )
上为单调函数,则实数a的取值范围可以是( )
 在
在 上为单调函数,则实数a的取值范围可以是( )
上为单调函数,则实数a的取值范围可以是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
抛物线 的准线与双曲线
的准线与双曲线 的两条渐近线所围成的三角形的面积等于( )
的两条渐近线所围成的三角形的面积等于( )
 的准线与双曲线
的准线与双曲线 的两条渐近线所围成的三角形的面积等于( )
的两条渐近线所围成的三角形的面积等于( )
A .  B .
B . 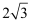 C . 2
D .
C . 2
D . 
 B .
B . 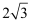 C . 2
D .
C . 2
D . 
已知向量  ,如果
,如果  ,那么 ( )
,那么 ( )
 ,如果
,如果  ,那么 ( )
,那么 ( )
A .  且
且  与
与  反向
B .
反向
B .  且
且  与
与  同向
C .
同向
C .  且
且  与
与  反向
D .
反向
D .  且
且  与
与  同向
同向
 且
且  与
与  反向
B .
反向
B .  且
且  与
与  同向
C .
同向
C .  且
且  与
与  反向
D .
反向
D .  且
且  与
与  同向
同向
如图,在三棱锥  中,平面
中,平面  平面
平面  ,
,  为等边三角形,
为等边三角形,  ,
,  是
是  的中点.
的中点.
 中,平面
中,平面  平面
平面  ,
,  为等边三角形,
为等边三角形,  ,
,  是
是  的中点.
的中点. 
-
(1) 证明:
 ;
;
-
(2) 若
 ,求
,求  到平面
到平面  的距离.
的距离.
如果  ,那么下列不等式中错误的是( )
,那么下列不等式中错误的是( )
 ,那么下列不等式中错误的是( )
,那么下列不等式中错误的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,若D为BC的中点,则有![]() ),将此结论类比到四面体中,在四面体A-BCD中,若G为△BCD的重心,则可得一个类比结论: .
),将此结论类比到四面体中,在四面体A-BCD中,若G为△BCD的重心,则可得一个类比结论: .
某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系式y=ekx+b(e为自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是( )
A.16小时 B.20小时
C.24小时 D.28小时
已知锐角 的内角
的内角 ,
,  ,
,  所对的边分别为
所对的边分别为 ,
,  ,
,  ,且
,且 ,
,  .
.
(1)求角 的大小;
的大小;
(2)求 的取值范围.
的取值范围.
(1)求角
(2)求
最近更新
- 在自然界中以游离态存在的金属是( ) A.钠 B.镁 C.铝
- 在我国南海某海域探明可燃冰储量约有194亿立方米.194亿用科学记数法表示为() A.1.94×1010 B.0.194
- 通过北宋“交子”和张择端《清明上河图》了解历史的方法 A.解读文物 B.查阅文献 C.考古发
- 长江中下游平原与四川盆地的大致界线是 A.秦岭 B.大兴安岭 C.大别山 D.巫山
- 已知数列、都是公差为1的等差数列,其首项分别为、,且,,,则数列前10项的和等于 A.55 B
- 神经系统中,专门调节心跳、血压等重要生命活动的神经传导中枢在:
- 关于岩石圈的叙述,正确的是 A.位于地面以下,古登堡界面以上 B.由地壳层和地幔的一部分组成 C.位于地
- 阅读下面一首清诗,回答问题。(6分)客发笤溪①叶燮②客心如水水如愁,容易归帆趁疾流。忽讶船窗送吴语,故山月已挂船头。【注
- 已知热化学方程式:C2H2(g)+O2(g)=2CO2(g)+H2O(g)H=-1256 kJ·mol-1。下列说法正确
- 从如图所示的实验中,可以直接得出的结论是A. 单侧光照引起生长素分布不均 B.感受光刺激的部位是上胚轴切段的顶端 C.生
- 阅读下面的文字,根据要求写一篇不少于800字的作文。我是一棵树,一棵长在房前屋后的树。我不知道从哪里来,也不知道自己能做
- (8分) 如图所示,两根平行光滑金属导轨竖直放置在匀强磁场中,磁场方向跟导轨所在平面垂直,金属棒ab 两端套在导轨上且可
- 若下图表示海陆间水循环的模式图,则最能代表台风登陆我国 的环节是: A.① B.② C.
- 20世纪80年代,英国首相撒切尔夫人说,社会有一个梯子和一张安全网;梯子用来供人们自己努力改善生活,安全网则用来防止人们
- 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“
- 如图所示,在网球的网前截击练习中,若练习者在球网正上方距地面H处,将球以某一速度沿垂直球网的方向击出,球刚好落在底线上,
- 阅读下文,并回答问题。 把菠菜叶放进适当的溶液中,进行研磨,将研磨液用纱布过滤后,除去未磨碎的组织,得到一种绿色的液体。
- 北京大学法学院五位教授以公民的名义致信全国人大常委会,要求对拆迁条例的合法性进行审查,建议废止或修改《城市房屋拆迁管理
- 如图表示某植物的非绿色器官在氧浓度为a、b、c、d时,CO2释放量和O2吸收量的变化.下列相关叙述,正确的是()A.氧浓
- 元宵节是中华民族重要的传统节日。下面是两副元宵节对联的上联,请参照示例,然后根据对联的基本要求,选出其中的一副对出下联。



