高中 数学
在①: 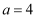 ,
,  ;②:
;②: 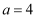 ,
,  为等腰三角形,这两个条件中任选一个,补充在下面的问题中,并进行解答.
为等腰三角形,这两个条件中任选一个,补充在下面的问题中,并进行解答.
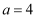 ,
,  ;②:
;②: 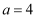 ,
,  为等腰三角形,这两个条件中任选一个,补充在下面的问题中,并进行解答.
为等腰三角形,这两个条件中任选一个,补充在下面的问题中,并进行解答. 在  中,已知 , 且
中,已知 , 且  ,求:
,求:
-
(1)
 的值;
的值;
-
(2)
 的面积.
的面积.
如图,菱形OBCD的顶点O与坐标原点重合,一边在x轴的正半轴上,已知∠BOD=60°,求菱形各边和两条对角线所在直线的倾斜角及斜率.

已知两动圆F1:(x+  )2+y2=r2和F2:(x﹣
)2+y2=r2和F2:(x﹣  )2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A,B满足:
)2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A,B满足:  =0.
=0.
 )2+y2=r2和F2:(x﹣
)2+y2=r2和F2:(x﹣  )2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A,B满足:
)2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A,B满足:  =0.
=0.
-
(1) 求曲线C的方程;
-
(2) 证明直线AB恒经过一定点,并求此定点的坐标;
-
(3) 求△ABM面积S的最大值.
已知函数  ,若存在
,若存在  ,
,  ,当
,当  时,
时,  ,则
,则  的取值范围为( )
的取值范围为( )
 ,若存在
,若存在  ,
,  ,当
,当  时,
时,  ,则
,则  的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D .
已知 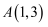 ,
,  ,求:
,求:
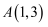 ,
,  ,求:
,求:
-
(1)
 ,
,  两点间的距离;
两点间的距离;
-
(2) 线段
 的垂直平分线方程.
的垂直平分线方程.
设椭圆  的左、右焦点分别为
的左、右焦点分别为  ,
,  ,上顶点为
,上顶点为  ,过点
,过点  与
与  垂直的直线交
垂直的直线交  轴负半轴于点
轴负半轴于点  ,且
,且  ,过
,过  ,
,  三点的圆恰好与直线
三点的圆恰好与直线  相切.
相切.
 的左、右焦点分别为
的左、右焦点分别为  ,
,  ,上顶点为
,上顶点为  ,过点
,过点  与
与  垂直的直线交
垂直的直线交  轴负半轴于点
轴负半轴于点  ,且
,且  ,过
,过  ,
,  三点的圆恰好与直线
三点的圆恰好与直线  相切.
相切.
-
(1) 求椭圆
 的方程;
的方程;
-
(2) 过右焦点
 作斜率为
作斜率为  的直线
的直线  与椭圆
与椭圆  交于
交于 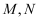 两点,问在
两点,问在  轴上是否存在点
轴上是否存在点  ,使得以
,使得以  为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出  的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
已知函数  的最小正周期为
的最小正周期为  .
.
 的最小正周期为
的最小正周期为  .
.
-
(1) 求
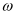 的值;
的值;
-
(2) 将函数
 的图象上各点的横坐标扩大为原来的2倍,纵坐标扩大为原来的
的图象上各点的横坐标扩大为原来的2倍,纵坐标扩大为原来的  倍,得到函数
倍,得到函数  ,若
,若  ,求
,求  的取值范围.
的取值范围.
已知数列 满足:
满足: ,
, ,若
,若 ,
, ,且数列
,且数列 的单调递增数列,则实数
的单调递增数列,则实数 的取值范围为( )
的取值范围为( )
 满足:
满足: ,
, ,若
,若 ,
, ,且数列
,且数列 的单调递增数列,则实数
的单调递增数列,则实数 的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若 , 则
, 则 ( )
( )
 , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量  =(2,1),
=(2,1),  =(1,2),则
=(1,2),则  ,
,  夹角的余弦值是( )
夹角的余弦值是( )
 =(2,1),
=(2,1),  =(1,2),则
=(1,2),则  ,
,  夹角的余弦值是( )
夹角的余弦值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在正四面体  中,
中,  为
为  的中点,则直线
的中点,则直线 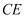 与直线
与直线  所成角的余弦值为( )
所成角的余弦值为( )
 中,
中,  为
为  的中点,则直线
的中点,则直线 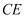 与直线
与直线  所成角的余弦值为( )
所成角的余弦值为( )
A .  B .
B . 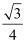 C .
C .  D .
D . 
 B .
B . 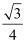 C .
C .  D .
D . 
“  ”是“
”是“  ”的( )
”的( )
 ”是“
”是“  ”的( )
”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
若x , y满足x+1  ,则2y - x的最小值是
,则2y - x的最小值是
 ,则2y - x的最小值是
,则2y - x的最小值是
函数  的部分图象大致为( )
的部分图象大致为( )
 的部分图象大致为( )
的部分图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知定义在R上的函数  的导函数为
的导函数为  ,且满足
,且满足  ,
,  ,则不等式
,则不等式  的解集为( )
的解集为( )
 的导函数为
的导函数为  ,且满足
,且满足  ,
,  ,则不等式
,则不等式  的解集为( )
的解集为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知点P(x,y)在经过 两点的直线上,则
两点的直线上,则 的最小值为( )
的最小值为( )
 两点的直线上,则
两点的直线上,则 的最小值为( )
的最小值为( )
A .  B .
B .  C . 16
D . 不存在
C . 16
D . 不存在
 B .
B .  C . 16
D . 不存在
C . 16
D . 不存在
今年4月23日我市正式宣布实施“3+1+2”的高考新方案,“3”是指必考的语文、数学、外语三门学科,“1”是指在物理和历史中必选一科,“2”是指在化学、生物、政治、地理四科中任选两科.为了解我校高一学生在物理和历史中的选科意愿情况,进行了一次模拟选科.已知我校高一参与物理和历史选科的有1800名学生,其中男生1000人,女生800人.按分层抽样的方法从中抽取了36个样本,统计知其中有17个男生选物理,6个女生选历史.
(Ⅰ)根据所抽取的样本数据,填写答题卷中的列联表.并根据K2统计量判断能否有90%的把握认为选择物理还是历史与性别有关?
(Ⅱ)在样本里选历史的人中任选4人,记选出4人中男生有X人,女生有Y人,求随机变量ξ=X﹣Y的分布列和数学期望.
K2的计算公式:
临界值表如下:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
已知函数![]()
(1)解不等式![]() ;
;
(2)若对![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的取值范围
的取值范围
已知二次函数![]() 对任意
对任意![]() 都有
都有![]() <0且
<0且![]() =
=![]() 成立,设向量
成立,设向量
![]() ,b=(2sin
,b=(2sin![]() ,
,![]() ),c=(
),c=(![]() ,1),d=(1,2),当
,1),d=(1,2),当![]() 是三角形内角时,求不等式
是三角形内角时,求不等式![]() (
(![]() ・b)>
・b)>![]() (c・d)的解集.
(c・d)的解集.
已知函数
(1)若函数![]() 在
在![]() 处取得极值,求a的值.
处取得极值,求a的值.
(2)讨论函数![]() 的单调性;
的单调性;
最近更新
- 做平抛运动的物体,在水平方向通过的最大距离取决于 ( )A.物体的高度和受到的重力 B.物体受到
- 当公共权力被滥用,政府官员不尽职时,作为公民,应当立即举起手中的利剑,依法同腐败分子作斗争。这里,公民能够立即举起的利剑
- 如图所示,根据通电螺线管的磁感线方向,可判断通电螺线管左端为______极,电源的a端为______极,小磁针静止时的b
- 下列各句中加线的成语使用恰当的一句是( ) A.她的小学和初中的都是在很普通的学校里上的,虽然师出无名,但今天她却成了
- 颇具人文关怀色彩的居民身份证法,加强了对公民个人信息的保护,明确规定警察不能随意检查居民的身份证。这种“以人为本”“与民
- 判断在下列装置中电流表能发生偏转的是( )
- 某中学对该校初一的学生就阅读“爱国题材”作品的情况进行调查,统计结果如下:(4分)我校中学生爱国意识调查表如何看待每周的
- 两个不共线向量,的夹角为,分别为与的中点,点在直线 上,且,则的最小值为( )
- 2010年9月,以1975年前后那段贫穷而饱含理想的时光为主线的电影《山楂树之恋》热播,引起了很大的社会反响,被称为“史
- 在河北承德普陀宗乘之庙的碑亭里,竖立着《土尔扈特全部归顺记》这块巨大的石碑。碑文记叙了土尔扈特蒙古部族在远离放土一百四十
- 质量为20g的小球,以20m/s水平速度与竖直墙碰撞后,仍以20m/s的水平速度反弹。在这过程中,小球动量变化的大小为_
- 某天然矿泉水的主要成份如下,请认真阅读后填空。 主要成分(mg/L): 碳酸氢根(HCO3-):173—205 氯
- 莫言的文学创作拥有深厚的地域和民间渊源,他以丰富的想像力,将魔幻现实主义与民间故事融会在一起,从“高密东北乡”的历史与现
- A healthy dose of sunshine may be the secret to staying youn
- 鼻腔中鼻毛的作用是 A.消化病菌
- 下列现象中与表面张力有关的是A.水中的气泡呈球形B.草叶上的露珠呈球形C.刚洗完头,头发粘在一起D.木块浮在水中
- 受海陆的影响,同一纬度的海洋和陆地气温不同。那么,下列说法中错误的是( ) A.夏季陆地气温高 B.夏季海洋气温低
- 纯铁的熔点为1535℃,而高炉中炼铁的生铁(含碳量较高的铁的合金)在1200℃左右就熔化了,这是因为 A.铁的纯度越高熔
- 一首诗:“粤海销烟扬我威,但悲港岛易英徽。前仇旧恨今尽雪,只缘华夏已腾飞。”诗中涉及的历史事件有 ①虎门销烟 ②签订《南
- 如图3-2-2所示,小车上固定着一根弯成α角的曲杆,杆的另一端固定一个有质量的小球m,试分析下列情况下杆对球的弹力的大致



