高中 数学
某学校组织的数学赛中,学生的竞赛成绩X服从正态分布X~N(100,σ2),P(X>120)=a,P(80≤X≤100)=b,则  的最小值为( )
的最小值为( )
 的最小值为( )
的最小值为( )
A . 8
B . 9
C . 16
D . 18
在直角坐标系  中,曲线
中,曲线  的参数方程为
的参数方程为  (其中
(其中  为参数),则曲线
为参数),则曲线  的直角坐标方程为.
的直角坐标方程为.
 中,曲线
中,曲线  的参数方程为
的参数方程为  (其中
(其中  为参数),则曲线
为参数),则曲线  的直角坐标方程为.
的直角坐标方程为.
已知函数  为奇函数.
为奇函数.
 为奇函数.
为奇函数.
-
(1) 求
 的值;
的值;
-
(2) 用定义法证明
 在R上为增函数;
在R上为增函数;
-
(3) 解不等式
 .
.
已知函数f(x)=ax(a>0且a≠1)的图象经过点(2, 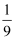 ).
).
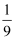 ).
).
-
(1) 求a的值;
-
(2) 比较f(2)与f(b2+2)的大小;
-
(3) 求函数f(x)=a
 (x≥0)的值域.
(x≥0)的值域.
如图,已知正三棱柱  (底面
(底面  是正三角形,侧棱与底面垂直),
是正三角形,侧棱与底面垂直),  ,
,  ,
,  分别是
分别是  ,
,  的中点.
的中点.
 (底面
(底面  是正三角形,侧棱与底面垂直),
是正三角形,侧棱与底面垂直),  ,
,  ,
,  分别是
分别是  ,
,  的中点.
的中点. 
-
(1) 证明:
 平面
平面  ;
;
-
(2) 求三棱锥
 的体积.
的体积.
已知函数f(x)=lnx﹣ax+  ﹣1(a∈R).
﹣1(a∈R).
 ﹣1(a∈R).
﹣1(a∈R).
-
(1) 当a≤
 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;
-
(2) 设g(x)=x2﹣2x+b.当a=
 时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.
函数  的图象可能是( )
的图象可能是( )
 的图象可能是( )
的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在三棱锥  中,
中,  平面
平面  ,
,  ,
,  ,则该三棱锥的外接球表面积为.
,则该三棱锥的外接球表面积为.
 中,
中,  平面
平面  ,
,  ,
,  ,则该三棱锥的外接球表面积为.
,则该三棱锥的外接球表面积为.
下列函数中,是偶函数且在区间  上单调递减的函数是( )
上单调递减的函数是( )
 上单调递减的函数是( )
上单调递减的函数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)=.
已知全集  ,集合
,集合  ,则
,则  图中阴影部分所表示的集合是( )
图中阴影部分所表示的集合是( )
 ,集合
,集合  ,则
,则  图中阴影部分所表示的集合是( )
图中阴影部分所表示的集合是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知a>0,b>0,a+b=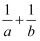 , 则
, 则 的最小值为( )
的最小值为( )
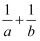 , 则
, 则 的最小值为( )
的最小值为( )
A . 4
B . 2 C . 8
D . 16
C . 8
D . 16
 C . 8
D . 16
C . 8
D . 16
设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示.

-
(1) 求A,ω,φ的值;
-
(2) 设θ为锐角,且f(θ)=﹣
 ,求f(θ﹣
,求f(θ﹣  )的值.
)的值.
如图,在正方体  中,
中,  平面
平面  ,垂足为H,给出下面结论:
,垂足为H,给出下面结论:
 中,
中,  平面
平面  ,垂足为H,给出下面结论:
,垂足为H,给出下面结论: ①直线  与该正方体各棱所成角相等;②直线
与该正方体各棱所成角相等;②直线  与该正方体各面所成角相等;③过直线
与该正方体各面所成角相等;③过直线  的平面截该正方体所得截面为平行四边形;④垂直于直线
的平面截该正方体所得截面为平行四边形;④垂直于直线  的平面截该正方体,所得截面可能为五边形,其中正确结论的序号为( )
的平面截该正方体,所得截面可能为五边形,其中正确结论的序号为( )

A . ①③
B . ②④
C . ①②④
D . ①②③
若函数  的图象向左平移
的图象向左平移  个单位,得到的函数图象的对称中心与f(x)图象的对称中心重合,则ω的最小值是( )
个单位,得到的函数图象的对称中心与f(x)图象的对称中心重合,则ω的最小值是( )
 的图象向左平移
的图象向左平移  个单位,得到的函数图象的对称中心与f(x)图象的对称中心重合,则ω的最小值是( )
个单位,得到的函数图象的对称中心与f(x)图象的对称中心重合,则ω的最小值是( )
A . 1
B . 2
C . 4
D . 8
从甲口袋摸出一个红球的概率是 , 从乙口袋中摸出一个红球的概率是
, 从乙口袋中摸出一个红球的概率是 , 则
, 则 是( )
是( )
 , 从乙口袋中摸出一个红球的概率是
, 从乙口袋中摸出一个红球的概率是 , 则
, 则 是( )
是( )
A . 2个球不都是红球的概率
B . 2个球都是红球的概率
C . 至少有一个红球的概率
D . 2个球中恰好有1个红球的概率
若函数f(x)=  x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
 x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
A . (1,2)
B . [1,2)
C . [0,2)
D . (0,2)
![]() 如图1所示,直角边
如图1所示,直角边![]() ,
,![]() ,
, ![]() 点是斜边BC上的动点,
点是斜边BC上的动点,![]() 交于点
交于点![]() ,
,![]() 交 于点
交 于点![]() . 设
. 设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,则
,则![]() 关于
关于![]() 的函数
的函数![]() ___
___

数列![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)等差数列![]() 成等比数列,求Tn.
成等比数列,求Tn.
若函数![]() 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在![]() 上是增函数,
上是增函数,![]() ,则使得
,则使得![]() 的
的![]() 的取值范围是______
的取值范围是______
最近更新
- 能正确表示下列化学反应的离子方程式的是( ) A.氧化钙与稀盐酸反应:CaO+2H+=Ca2++H2O B.稀氨水
- 2008年10月6日,为进一步做好普通发票防伪印制工作,南昌市国税局决定近期对有奖发票进行全面改版。通过采用防伪用纸、票
- 下列有关我国三个经济地带产业结构的叙述,正确的是( ) A. 中部地带第一产业比重最大 B. 东部
- Please ____ the jacket to your father this afternoon.
- 我国居民的消费水平在逐步提高,从根本上说取决于 A.收入水平 B.物价水平 C.人口数量 D.国
- 马克思主义中国化的三大理论成果是 ①思想 ②理论 ③党的基本路线 ④“三个代表”的重要思想 A、①
- 编写一个程序,要求输入两个正数a和b的值,输出ab和ba的值.
- 第四部分 写作(共三节,满分35分) 第一节 单词拼写(把完整的单词写在答题卡上) 71. Every body kn
- 下图表示细胞内遗传信息传递的某个阶段,其中①②③分别表示相应的结构或物质,Asn、Ser、Cly为三种氨基酸,分别是天冬
- 光在透明物质或中传播,声音的传播需要 。
- 在泡菜腌制过程中亚硝酸盐含量变化曲线如图所示,正确的是() A. B. C. D.
- 下列关于人类遗传病的说法,正确的是 A.单基因遗传病是受1个基因控制的遗传病 B.镰刀型细胞贫血症的人与正常人相比,有关
- 日常生活中发生的下列变化都属于化学变化的一组是() A.玻璃杯被摔碎,米饭变馊 B.酒精挥发,湿衣服晾干 C.蜡烛燃
- 已知P为⊙O内一点,OP=1,如果⊙O的半径是2,那么过P点的最短弦长是 ( ) A.1
- 一切陆生生物的“立足点”是A、大气圈 B、水圈 C、岩石圈 D、生物圈
- 木工师傅做完房门后,为防止变形钉上两条斜拉的木条这样做的根据是
- 物体在光滑斜面顶端由静止开始匀加速下滑,最初4s内经过的位移为S1,最后4s内经过的位移为S2,且S2-S1=8m,S1
- 下面四幅地形剖面图中,能正确表示湖南省沿28°N线地形起伏的是
- 地球同步卫星每天绕地球运转一周,月球这颗地球的天然卫星27天 绕地 球运转一周,则月球绕地球运转的轨道半径是同步卫星轨
- 维新运动期间,宣扬维新思想的学会、学堂在全国各地纷纷兴起。其中,创办于湖南长沙的是( ) A.保国会



