高中 数学
已知函数f(x)=x3  (1﹣a)x2﹣3ax+1,a>0.
(1﹣a)x2﹣3ax+1,a>0.
 (1﹣a)x2﹣3ax+1,a>0.
(1﹣a)x2﹣3ax+1,a>0.
-
(1) 试讨论f(x)(x≥0)的单调性;
-
(2) 证明:对于正数a,存在正数p,使得当x∈[0,p]时,有﹣1≤f(x)≤1;
-
(3) 设(1)中的p的最大值为g(a),求g(a)的最大值.
已知函数  =f(2x)
=f(2x)
 =f(2x)
=f(2x)
-
(1) 用定义证明函数g(x)在(﹣∞,0)上为减函数.
-
(2) 求g(x)在(﹣∞,﹣1]上的最小值.
若二次函数满足  ,且
,且 
 ,且
,且 
-
(1) 求
 的解析式;
的解析式;
-
(2) 设
 ,求
,求  在
在  上的最小值
上的最小值  的解析式.
的解析式.
定义在R上的函数f(x)满足:f(1)=1,且对于任意的x∈R,都有f′(x)<  ,则不等式f(log2x)>
,则不等式f(log2x)>  的解集为.
的解集为.
 ,则不等式f(log2x)>
,则不等式f(log2x)>  的解集为.
的解集为.
已知公差不为零的等差数列 与公比为q的等比数列
与公比为q的等比数列 有相同的首项,同时满足
有相同的首项,同时满足 ,
,  ,
,  成等比,
成等比, ,
,  ,
,  成等差,则
成等差,则 =( )
=( )
 与公比为q的等比数列
与公比为q的等比数列 有相同的首项,同时满足
有相同的首项,同时满足 ,
,  ,
,  成等比,
成等比, ,
,  ,
,  成等差,则
成等差,则 =( )
=( )
A .  B .
B .  C .
C .  D .
D . 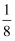
 B .
B .  C .
C .  D .
D . 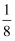
某高速公路隧道内设双行线公路,其截面由一段圆弧和一个长方形的三边构成(如图所示).已知隧道总宽度  为
为  ,行车道总宽度
,行车道总宽度  为
为  ,侧墙面高
,侧墙面高  ,
,  为
为  ,弧顶高
,弧顶高  为
为  .
.
 为
为  ,行车道总宽度
,行车道总宽度  为
为  ,侧墙面高
,侧墙面高  ,
,  为
为  ,弧顶高
,弧顶高  为
为  .
.

-
(1) 建立适当的直角坐标系,求圆弧所在的圆的方程.
-
(2) 为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有
 .请计算车辆通过隧道的限制高度是多少.
.请计算车辆通过隧道的限制高度是多少.
已知函数  的图像过点
的图像过点  .
.
 的图像过点
的图像过点  .
.
-
(1) 求实数m的值;
-
(2) 求不等式
 的解集.
的解集.
如图,已知  是圆柱
是圆柱  的轴截面,
的轴截面,  、
、 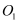 分别是两底面的圆心,
分别是两底面的圆心,  是弧
是弧  上的一点,
上的一点,  ,圆柱的体积和侧面积均为
,圆柱的体积和侧面积均为 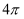 .
.
 是圆柱
是圆柱  的轴截面,
的轴截面,  、
、 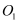 分别是两底面的圆心,
分别是两底面的圆心,  是弧
是弧  上的一点,
上的一点,  ,圆柱的体积和侧面积均为
,圆柱的体积和侧面积均为 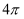 .
.

-
(1) 求证:平面
 平面
平面  ;
;
-
(2) 求二面角
 的大小.
的大小.
设sin( +θ)=
+θ)= , 则sin2θ=( )
, 则sin2θ=( )
 +θ)=
+θ)= , 则sin2θ=( )
, 则sin2θ=( )
A . - B . -
B . - C .
C .  D .
D . 
 B . -
B . - C .
C .  D .
D . 
直线 的倾斜角是( )
的倾斜角是( )
 的倾斜角是( )
的倾斜角是( )
A .  -arctan
-arctan B .
B .  -arctan
-arctan C .
C .  D .
D . 
 -arctan
-arctan B .
B .  -arctan
-arctan C .
C .  D .
D . 
设向量  ,
,  不共线,若
不共线,若  ,则实数λ的值为.
,则实数λ的值为.
 ,
,  不共线,若
不共线,若  ,则实数λ的值为.
,则实数λ的值为.
成都市现在已是拥有1400多万人口的城市,机动车保有量已达450多万辆,成年人中约 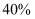 拥有机动车驾驶证.为了解本市成年人的交通安全意识情况,某中学的同学利用国庆假期进行了一次全市成年人安全知识抽样调查.先根据是否拥有驾驶证,用分层抽样的方法抽取了200名成年人,然后对这200人进行问卷调查.这200人所得的分数都分布在
拥有机动车驾驶证.为了解本市成年人的交通安全意识情况,某中学的同学利用国庆假期进行了一次全市成年人安全知识抽样调查.先根据是否拥有驾驶证,用分层抽样的方法抽取了200名成年人,然后对这200人进行问卷调查.这200人所得的分数都分布在  范围内,规定分数在80以上(含80)的为“具有很强安全意识”,所得分数的频率分布直方图如图所示.
范围内,规定分数在80以上(含80)的为“具有很强安全意识”,所得分数的频率分布直方图如图所示.
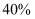 拥有机动车驾驶证.为了解本市成年人的交通安全意识情况,某中学的同学利用国庆假期进行了一次全市成年人安全知识抽样调查.先根据是否拥有驾驶证,用分层抽样的方法抽取了200名成年人,然后对这200人进行问卷调查.这200人所得的分数都分布在
拥有机动车驾驶证.为了解本市成年人的交通安全意识情况,某中学的同学利用国庆假期进行了一次全市成年人安全知识抽样调查.先根据是否拥有驾驶证,用分层抽样的方法抽取了200名成年人,然后对这200人进行问卷调查.这200人所得的分数都分布在  范围内,规定分数在80以上(含80)的为“具有很强安全意识”,所得分数的频率分布直方图如图所示.
范围内,规定分数在80以上(含80)的为“具有很强安全意识”,所得分数的频率分布直方图如图所示. 
| 拥有驾驶证 | 没有驾驶证 | 总计 | |
| 具有很强安全意识 | |||
| 不具有很强安全意识 | 58 | ||
| 总计 | 200 |
-
(1) 补全上面的
 列联表,并判断能否有超过
列联表,并判断能否有超过  的把握认为“具有很强安全意识”与拥有驾驶证有关?
的把握认为“具有很强安全意识”与拥有驾驶证有关?
-
(2) 将上述调查所得的频率视为概率,现从全市成年人中随机抽取4人,记“具有很强安全意识”的人数为X,求X的分布列及数学期望.
附表及公式:
 ,其中
,其中  .
.P(
 )
)0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
公元五世纪,数学家祖冲之估计圆周率 的范围是:
的范围是: , 为纪念祖冲之在圆周率方面的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字的个数为( )
, 为纪念祖冲之在圆周率方面的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字的个数为( )
 的范围是:
的范围是: , 为纪念祖冲之在圆周率方面的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字的个数为( )
, 为纪念祖冲之在圆周率方面的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字的个数为( )
A . 720
B . 1440
C . 2280
D . 4080
凸十边形的对角线的条数为( )
A . 10
B . 35
C . 45
D . 90
如图所示:若△ABC中,∠ACB=90°,∠BAC=60°,AB=8,PC⊥平面ABC,PC=4,M是AB上一点,则PM的最小值为__________。

若命题p:![]() ,
,![]() ,则
,则![]() 是______.
是______.
某学校随机抽查了本校20名同学,调查他们平均每天在课外从事体育锻炼的时间(单位:分钟),根据所得数据的茎叶图,以5为组距将数据分为8组:![]() ,作出频率分布直方图如图所示,则原始的茎叶图可能是
,作出频率分布直方图如图所示,则原始的茎叶图可能是
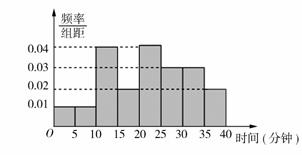
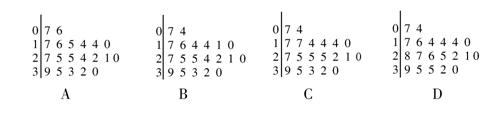
用6种颜色给右图四面体![]() 的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种
的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种
A.4080 B.3360 ![]() C. 1920 D. 720
C. 1920 D. 720
已知直线L过抛物线C的焦点,且与C的对称轴垂直,L与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )
A.18 B.24 C.36 D.48
![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- I think we ______ another planet to live on in future. A. ha
- 请结合下图所示实验装置回答有关问题: A B C
- It's no secret to us, but he alone is in the dark. It means
- 在世界各大洲中,人口增长率最高的大洲已经出现了众多的环境问题,其中最主要的环境问题是A.环境污染
- 下列符合商鞅变法“规定按军功授爵赐田”内容的是:( )A.商君相秦十年,宗室贵戚多怨望 B.戮力本业,
- 氮化铝(AlN)具有耐高温、抗冲击、导热性好等优良性质,被广泛应用于电子工业、陶瓷工业等领域。在一定条件下,氮化铝可通过
- 汽车前方120m有一自行车正以6m/s的速度匀速前进,汽车以18m/s的速度追赶自行车,若两车在同一条公路不同车道上作同
- An abandoned car in Chicagoworth about $600 has been issued
- 科斯定理(Coase theorem)是由罗纳德·科斯(Ronald Coase)提出的一种观点,认为在某些条件下,经济
- 现有一瓶某品牌的饮用纯净水。 (1)瓶盖上刻有一道道竖直的条纹,其目的是 摩擦(选填“增大”或“减
- 下列结构示意图表示的粒子中,属于阴离子的是() A. B. C. D.
- 据权威部门估算,2009年,大约有650万返乡农民工面临再就业问题,还有610万大学毕业生作为城镇新增就业的主要力量进入
- 下列物质在空气中最不容易燃烧的是( ) A.铁片 B.镁条 C.木炭 D.氢气
- 如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠ABD=( ) A. 20° B.
- 大文豪雨果说:“建筑是用石头写成的史书。”阅读材料,回答问题。 材料一 宗祠,是供奉祖先、举行祭祀活动的场所,又是从事家
- 有元索化合价升降的反应是氧化还原反应。下列属于氧化还原反应的是【 】 高温 A.C
- 下图是小梅配制100g溶质质量分数为12%的NaCl溶液的实验操作示意图: (1)上图中的玻璃仪器分别是广口瓶、量筒、烧
- SECTION C (25 points) Directions: Write an English compositi
- (本题满分为8分)已知,求(1);(2)的值.
- 一物体在多个恒力作用下做匀速直线运动,现撤去其中一个力,则在其以后的运动过程中速度大小v、动能EK的变化图象可能是



