高中 数学
在△ABC中,D是AB的中点,H是CD的中点,若  =λ
=λ  +μ
+μ  (x,μ∈R),则λ+μ=( )
(x,μ∈R),则λ+μ=( )
 =λ
=λ  +μ
+μ  (x,μ∈R),则λ+μ=( )
(x,μ∈R),则λ+μ=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 或
或  ,则
,则 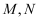 的大小关系为.
的大小关系为.
若数列 满足
满足 , 令
, 令 , 则
, 则 .
.
 满足
满足 , 令
, 令 , 则
, 则 .
.
已知函数 , 若方程
, 若方程 有三个不同的实数根,则实数
有三个不同的实数根,则实数 的取值范围是( )
的取值范围是( )
 , 若方程
, 若方程 有三个不同的实数根,则实数
有三个不同的实数根,则实数 的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  ,则
,则  的图象大致为( )
的图象大致为( )
 ,则
,则  的图象大致为( )
的图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设点A(﹣2,3),B(3,2),若直线ax+y+2=0与线段AB没有交点,则a的取值范围是( )
A . (﹣∞,﹣ 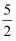 ]∪[
]∪[ 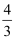 ,+∞)
B . (﹣
,+∞)
B . (﹣ 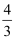 ,
, 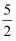 )
C . [﹣
)
C . [﹣ 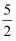 ,
, 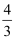 ]
D . (﹣∞,﹣
]
D . (﹣∞,﹣ 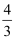 ]∪[
]∪[ 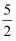 ,+∞)
,+∞)
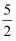 ]∪[
]∪[ 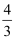 ,+∞)
B . (﹣
,+∞)
B . (﹣ 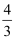 ,
, 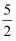 )
C . [﹣
)
C . [﹣ 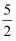 ,
, 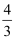 ]
D . (﹣∞,﹣
]
D . (﹣∞,﹣ 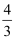 ]∪[
]∪[ 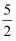 ,+∞)
,+∞)
以椭圆 的焦点为顶点,离心率为2的双曲线方程( )
的焦点为顶点,离心率为2的双曲线方程( )
 的焦点为顶点,离心率为2的双曲线方程( )
的焦点为顶点,离心率为2的双曲线方程( )
A .  B .
B .  C .
C .  或
或 D . 以上都不对
D . 以上都不对
 B .
B .  C .
C .  或
或 D . 以上都不对
D . 以上都不对
在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=  acosB.
acosB.
 acosB.
acosB.
-
(1) 求角B的大小;
-
(2) 若b=3,sinC=2sinA,求a,c的值
已知实数x,y满足  ,则z=x+2y的最小值为.
,则z=x+2y的最小值为.
 ,则z=x+2y的最小值为.
,则z=x+2y的最小值为.
若射手射击5次,每次命中的概率为0.6,则5次中有3次中靶的概率是( )
A . 0.6
B . 0.36
C . 0.216
D . 0.3456
已知函数f(x)=cosx,a,b,c分别为△ABC的内角A,B,C所对的边,且3a2+3b2﹣c2=4ab,则下列不等式一定成立的是( )
A . f(sinA)≤f(cosB)
B . f(sinA)≥f(cosB)
C . f(sinA)≥f(sinB)
D . f(cosA)≤f(cosB)
已知等比数列  的前
的前  项和
项和  ,其中
,其中  为实数.
为实数.
 的前
的前  项和
项和  ,其中
,其中  为实数.
为实数.
-
(1) 求实数
 的值,并求出数列
的值,并求出数列  的通项公式;
的通项公式;
-
(2) 求数列
 的前
的前  项的积
项的积  .
.
如图是一个几何体的正视图和俯视图.
(1)试判断该几何体是什么几何体?(不用说明理由)
(2)请在正视图的正右边画出其侧视图,并求该平面图形的面积;
(3)求出该几何体的体积与表面积。

设函数![]() ,
,![]() 若不存在
若不存在![]() ,使得
,使得![]() 与
与![]() 同时成立,则实数a的取值范围是________.
同时成立,则实数a的取值范围是________.
某射手射击所得环数X的分布列如下:
| X | 7 | 8 | 9 | 10 |
| P | x | 0.1 | 0.3 | y |
已知X的均值E(X)=8.9,则y的值为________.
七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图所示的是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自黑色部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
若![]() ,则
,则![]() 等于 .
等于 .
编号为1,2,3,4,5的五朵花分别放入编号为1,2,3,4,5的五个花瓶中,其中有且只有两朵花的编号与花瓶号一致的放法有
A.10种 B.20种 C.30种 D.60种
已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,且
,且![]() , 则满足
, 则满足![]() 的最小正整数
的最小正整数![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
设复数![]() 满足
满足![]() (
(![]() 为虚数单位),则复数
为虚数单位),则复数![]() 在复平面内对应的点位于( ).
在复平面内对应的点位于( ).
A. 第一象限 B. 第二象限 C.第三象限 D.第四象限
2、
最近更新
- 阅读下面的文字,完成下题。 “青蒿素之母”:屠呦呦 1930年,屠呦呦出生于浙江省宁波市。“呦呦鹿鸣,食野之苹”,父母选
- 关于欧洲联盟的表述不正确的是 A.成立于1993年 B.是欧洲国家的政治军事集团 C.
- 27. 20世纪初期,中国曾“以俄为师”。这里的“俄”通常是指( ) ①沙俄 ②苏俄 ③苏联 ④
- _____ surprised the family most was ________ the girl played
- 下列各句中,表述有误的一句是 A.华兹华斯是英国浪漫主义诗人,“湖畔派”的代表。 B.《左传》是我国第一部叙事详细的编年
- x 、y为两种元素的原子,x的阴离子与y的阳离子具有相同的电子层结构,由此可知( ) A.x的原子半径大于y的原子半径
- 在一瓶NaCl饱和溶液中,当温度不变时,加入少量NaCl晶体,则 A.溶液的质量增大 B.晶体的质量不变 C.
- 下列各组物质两两之间都能互相发生化学反应的是() A.C CuO H2SO4(稀) B.Ba(OH)2
- 有关我国季风的叙述,下列正确的是( ) A.影响我国的夏季风,既有来自太平洋的西南季风,也有来自印度洋的东南季风
- 下列各项因素中能够对化学反应速度起决定作用的是( ) A、温度 B、浓度 C、
- Cathy was a teacher from Newcastle, is almost as far n
- 若,则下列说法正确的是 ( ) A.若,则
- 学习不应有压力,我们不应给自己提出更高的要求,更不要自我加压。判断:( ) 理由:
- 在保护地球爱护家园活动中,校团委把一批树苗分给初三(1)班同学去栽种.如果每人分2棵,还剩42棵;如果前面每人分3棵,那
- 在同温同压下,关于等质量的CO2和SO2气体,下列说法不正确的是 ( )A.CO2和SO2的分子数比为16:1
- 2010年6月5日是第39个世界环境日,我国环保总局确定的主题是“低碳减排 绿色家园”。下列措施不符合这一主题的是A.推
- 诗歌赏析 江畔独步寻花 黄四娘家花满蹊,千朵万朵压枝低。留连戏蝶时时舞,自在娇莺恰恰啼。 (1)诗中哪两个字写出了花的繁
- ——We must thank you for taking the trouble to cook us a meal
- 下列气态氢化物最稳定的是 ( ) A.HCl B.HBr C.HF
- 下列物质中属于纯净物的是A.空气 B.粗盐 C.生铁 D.纯碱



