高中 数学
二项式(x+y)5的展开式中,含x2y3的项的系数是(用数字作答).
过抛物线y2=2px(p>0)的焦点F且倾斜角为120°的直线l与抛物线在第一、四象限分别交于A、B两点,则  的值等于( )
的值等于( )
 的值等于( )
的值等于( )
A . 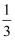 B .
B . 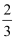 C .
C . 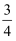 D .
D . 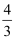
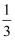 B .
B . 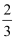 C .
C . 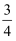 D .
D . 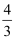
在 中,
中, , 且
, 且 ,
,  , 若将
, 若将 沿AC边上的中线BD折起,使得平面
沿AC边上的中线BD折起,使得平面 平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( )
平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( )
 中,
中, , 且
, 且 ,
,  , 若将
, 若将 沿AC边上的中线BD折起,使得平面
沿AC边上的中线BD折起,使得平面 平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( )
平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( )
A .  B . 四面体ABCD的体积为
B . 四面体ABCD的体积为 C . 存在点E使得
C . 存在点E使得 的面积为
的面积为 D . 四面体ABCD的外接球表面积为
D . 四面体ABCD的外接球表面积为
 B . 四面体ABCD的体积为
B . 四面体ABCD的体积为 C . 存在点E使得
C . 存在点E使得 的面积为
的面积为 D . 四面体ABCD的外接球表面积为
D . 四面体ABCD的外接球表面积为
某单位为了了解用电量y(度)与气温X(℃)之间的关系,随机统计了某4天的用电量与当天气温,并作了如下的对照表:由表中数据,得回归直线方程  =
=  +
+  ,若
,若  =﹣2,则
=﹣2,则  =( )
=( )
 =
=  +
+  ,若
,若  =﹣2,则
=﹣2,则  =( )
=( )气温X(℃) | 18 | 13 | 10 | ﹣1 |
用电量y | 24 | 34 | 38 | 64 |
A . 60
B . 58
C . 62
D . 64
已知平面向量  ,
,  的夹角为45°,
的夹角为45°,  且
且  ,则
,则  的最小值是.
的最小值是.
 ,
,  的夹角为45°,
的夹角为45°,  且
且  ,则
,则  的最小值是.
的最小值是.
方程2x2+(m+1)x+m=0有一正根一负根,则实数m的取值范围是.
平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(﹣1,3),若点C满足  =α
=α  +β
+β  ,其中α,β∈R,且α+β=1,则点C的轨迹形状是.
,其中α,β∈R,且α+β=1,则点C的轨迹形状是.
 =α
=α  +β
+β  ,其中α,β∈R,且α+β=1,则点C的轨迹形状是.
,其中α,β∈R,且α+β=1,则点C的轨迹形状是.
已知向量  ,函数
,函数  .
.
 ,函数
,函数  .
.
-
(1) 求函数f(x)的单调递减区间;
-
(2) 若
 ,且α为第一象限角,求cosα的值.
,且α为第一象限角,求cosα的值.
已知随机变量  服从正态分布
服从正态分布  ,
,  ,则
,则  .
.
 服从正态分布
服从正态分布  ,
,  ,则
,则  .
.
如图所示,  中,
中, 


 .
.
 中,
中, 


 .
. 
-
(1) 求AB;
-
(2) 求
 的值以及
的值以及  的面积.
的面积.
已知函数  ,则
,则  单调递增区间为;若函数
单调递增区间为;若函数  在区间
在区间  上单调,则
上单调,则  的取值范围为.
的取值范围为.
 ,则
,则  单调递增区间为;若函数
单调递增区间为;若函数  在区间
在区间  上单调,则
上单调,则  的取值范围为.
的取值范围为.
等差数列  的前四项之和为124,后四项之和为156,各项和为210,则此数列的项数为( )
的前四项之和为124,后四项之和为156,各项和为210,则此数列的项数为( )
 的前四项之和为124,后四项之和为156,各项和为210,则此数列的项数为( )
的前四项之和为124,后四项之和为156,各项和为210,则此数列的项数为( )
A . 5
B . 6
C . 7
D . 8
已知集合 ,
,  .
.
 ,
,  .
.
-
(1) 若
 , 求图中阴影部分
, 求图中阴影部分 ;
;

-
(2) 若
 , 求实数
, 求实数 的取值范围.
的取值范围.
 .
.
已知函数  ,相邻两个对称中心之间的距离为
,相邻两个对称中心之间的距离为  ,若将函数
,若将函数  的图象向左平移
的图象向左平移  个单位长度,得到的函数图象关于
个单位长度,得到的函数图象关于  轴对称,则函数
轴对称,则函数  在
在  上的最大值为( )
上的最大值为( )
 ,相邻两个对称中心之间的距离为
,相邻两个对称中心之间的距离为  ,若将函数
,若将函数  的图象向左平移
的图象向左平移  个单位长度,得到的函数图象关于
个单位长度,得到的函数图象关于  轴对称,则函数
轴对称,则函数  在
在  上的最大值为( )
上的最大值为( )
A .  B . 0
C .
B . 0
C .  D .
D . 
 B . 0
C .
B . 0
C .  D .
D . 
已知函数 ,
,  , 且
, 且 , 下列结论正确的是( )
, 下列结论正确的是( )
 ,
,  , 且
, 且 , 下列结论正确的是( )
, 下列结论正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
(本题满![]() 分12分)
分12分)
已知椭圆![]() 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点(4,0)且不与坐标轴垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .求证:直线
.求证:直线![]() 过
过![]() 轴上的一定点,并求出此定点坐标.
轴上的一定点,并求出此定点坐标.
在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() 成等差数列.
成等差数列.
(Ⅰ)求角![]() 的大小;(Ⅱ)若
的大小;(Ⅱ)若![]() ,求
,求![]() 边上中线长的最小值.
边上中线长的最小值.
已知实数![]() 满足
满足 ,求
,求![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
设 ,直线
,直线 和圆
和圆 (
( 为参数)相切,则
为参数)相切,则 的值为____.
的值为____.
最近更新
- _______, according to the instructions, the medicine, I thin
- (16分)如图,在倾角为θ的光滑斜面上,有两个用轻质弹簧相连接的物体A、B。它们的质量分别是MA和MB,弹簧的劲度系数K
- 十月革命是人类历史的伟大开端,它留下的深刻启示是( ) A.革命必须走城市道路 B.资本主义已
- 某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C
- 在固定体积的密闭容器中进行如下反应:2SO2(g) + O2(g) 2 SO3(g)。已知反应过程某一时刻SO2、O2
- 胡椒酚是植物挥发油的一种成分,关于胡椒酚的下列说法①该化合物属于芳香烃②分子中至少7个碳原子处在同一平面③它有顺反异物体
- (I)已知函数在上是增函数,求得取值范围; (II)在(I)的结论下,设,,求函数的最小值.
- 下列有关反应离子方程式错误的是 A.KOH溶液与过量的SO2反应: OH—+SO2==HSO3— B.Na2SO3溶液
- 一家商店某种裤子按成本价提高50%后标价,又以八折优惠卖出, 结果每条裤子获利10元,则这条裤子的成本是 。
- 根据玻尔理论,某原子的电子从能量为E的轨道跃迁到能量为E′的轨道,辐射出波长为λ的光.以h表示普朗克常量,c表示真空中的
- 某动物保护组织在我国云南寻找国家重点保护动物野牛时,根据采集到的某野牛留在沙地上的脚印,测出该野牛在水平沙地上站立时与地
- 1861年农奴制改革有利于提高农民生产的积极性,是因为①农民在法律上获得了人身自由 ②农民享有一定的公民权利 ③
- 科学家推测生命起源经理了四个化学进化过程,其中小分子有机物(如氨基酸)的形成和原始生命诞生的场所分别是( )A、原
- “它是我国一条重要的地理分界线,与800mm年等降水量线、一月0℃等温线经过的地区大致相当。”这条地理分界线是(
- 分封制和宗法制的共同点是突出强调( ) A、等级关系 B、血缘关系 C、臣属关系
- 已知,则 ▲ .
- 以下元素均为短周期元素:元素代号 相关信息 M 非金属元素,其气态氢化物的水溶液呈碱性 A A的单质与冷水剧烈反应,得到
- 《吴越春秋》记载:“(阖闾)请干将铸作名剑二枚。……干将作剑,……使童女童男三百人,鼓囊装炭,金铁乃濡,遂以成剑。”这表
- 阅读下面的文字,回答问题。 特别的礼物 郁葱/译 早上,阿尔琼被收音机定时的7点新闻闹醒。他摸着旁边空空的枕头,才想起妻
- 某有机物的结构简式为下列关于该有机物的叙述不正确的是( )A.能与金属钠发生反应并放出氢气B.能在催化剂作用下与H



