高中 数学
由曲线y=x2和曲线y=  围成的一个叶形图如图所示,则图中阴影部分面积为( )
围成的一个叶形图如图所示,则图中阴影部分面积为( )

A .  B .
B . 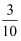 C .
C .  D .
D . 
 B .
B . 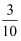 C .
C .  D .
D . 
椭圆 的离心率为( )
的离心率为( )
 的离心率为( )
的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
点  在双曲线
在双曲线  上,
上,  、
、  是双曲线的两个焦点,
是双曲线的两个焦点,  ,且
,且  的三条边长满足
的三条边长满足  ,则此双曲线的离心率是( )
,则此双曲线的离心率是( )
 在双曲线
在双曲线  上,
上,  、
、  是双曲线的两个焦点,
是双曲线的两个焦点,  ,且
,且  的三条边长满足
的三条边长满足  ,则此双曲线的离心率是( )
,则此双曲线的离心率是( )
A .  B .
B .  C . 2
D . 5
C . 2
D . 5
 B .
B .  C . 2
D . 5
C . 2
D . 5
在△ABC中,若 , 则△ABC的形状是( )
, 则△ABC的形状是( )
 , 则△ABC的形状是( )
, 则△ABC的形状是( )
A . 直角三角形
B . 等腰或直角三角形
C . 不能确定
D . 等腰三角形
函数  的最小正周期为4π,当f(x)取得最小值时,x的取值集合为( )
的最小正周期为4π,当f(x)取得最小值时,x的取值集合为( )
 的最小正周期为4π,当f(x)取得最小值时,x的取值集合为( )
的最小正周期为4π,当f(x)取得最小值时,x的取值集合为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B . {2}
C . {-2}
D . {-1}
B . {2}
C . {-2}
D . {-1}
 B . {2}
C . {-2}
D . {-1}
B . {2}
C . {-2}
D . {-1}
设函数f(x)=  则f[f(﹣1)]的值为.
则f[f(﹣1)]的值为.
 则f[f(﹣1)]的值为.
则f[f(﹣1)]的值为.
设直线m,n和平面 , 下列四个命题中,正确的是( )
, 下列四个命题中,正确的是( )
 , 下列四个命题中,正确的是( )
, 下列四个命题中,正确的是( )
A . 若 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 则
则
 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 则
则
由直线y=x+1上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
A . 1
B .  C .
C .  D . 3
D . 3
 C .
C .  D . 3
D . 3
已知函数  ,若曲线
,若曲线  在点
在点  处的切线的斜率为2,则数
处的切线的斜率为2,则数  的值是.
的值是.
 ,若曲线
,若曲线  在点
在点  处的切线的斜率为2,则数
处的切线的斜率为2,则数  的值是.
的值是.
已知双曲线  ﹣
﹣  =1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.
=1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.
 ﹣
﹣  =1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.
=1(a>0,b>0)的一条渐近线经过点(1,2),则该渐近线与圆(x+1)2+(y﹣2)2=4相交所得的弦长为.
已知数列  的前
的前  项和为
项和为  ,首项
,首项  ,
,  .
.
 的前
的前  项和为
项和为  ,首项
,首项  ,
,  .
.
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 设
 ,记数列
,记数列  的前
的前  项和为
项和为  ,是否存在正整数
,是否存在正整数  ,使得
,使得  ?若存在,求出
?若存在,求出  的值;若不存在,说明理由.
的值;若不存在,说明理由.
函数
 的零点的个数为( )
的零点的个数为( )

 的零点的个数为( )
的零点的个数为( )
A . 0个
B . 1个
C . 2个
D . 3个
设函数  ,则
,则  .
.
 ,则
,则  .
.
正方体 中,
中, ,
,  分别为棱
分别为棱 和
和 的中点,则下列说法正确的是( )
的中点,则下列说法正确的是( )
 中,
中, ,
,  分别为棱
分别为棱 和
和 的中点,则下列说法正确的是( )
的中点,则下列说法正确的是( )
A .  平面
平面 B .
B .  平面
平面 C . 异面直线
C . 异面直线 与
与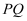 所成角为90°
D . 平面
所成角为90°
D . 平面 截正方体所得截面为等腰梯形
截正方体所得截面为等腰梯形
 平面
平面 B .
B .  平面
平面 C . 异面直线
C . 异面直线 与
与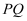 所成角为90°
D . 平面
所成角为90°
D . 平面 截正方体所得截面为等腰梯形
截正方体所得截面为等腰梯形
点A,B,C,D在同一个球的球面上,AB=BC=1,∠ABC=120°,若四面体ABCD体积的最大值为  ,则这个球的表面积为( )
,则这个球的表面积为( )
 ,则这个球的表面积为( )
,则这个球的表面积为( )
A .  B . 4π
C .
B . 4π
C .  D .
D . 
 B . 4π
C .
B . 4π
C .  D .
D . 
已知实数![]() ,对于定义在R上的函数
,对于定义在R上的函数![]() ,有下述命题:
,有下述命题:
①“![]() 是奇函数”的充要条件是“函数
是奇函数”的充要条件是“函数![]() 的图像关于点
的图像关于点![]() 对称”;
对称”;
②“![]() 是偶函数”的充要条件是“函数
是偶函数”的充要条件是“函数![]() 的图像关于直线
的图像关于直线![]() 对称”;
对称”;
③“![]() 是
是![]() 的一个周期”的充要条件是“对任意的
的一个周期”的充要条件是“对任意的![]() ,都有
,都有![]() ”;
”;
④ “函数![]() 与
与![]() 的图像关于
的图像关于![]() 轴对称”的充要条件是“
轴对称”的充要条件是“![]() ”
”
其中正确命题的序号是( )
A.①② B.②③ C.①④ D.③④
某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
|
| 2 | 4 | 5 | 6 | 8 |
|
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图:
(2)求回归直线方程;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
高三毕业时,甲,乙,丙等五位同学站成一排合影留念,已知甲,乙相邻,则甲丙
相邻的概率为 .
函数![]() 的单调减区间_________
的单调减区间_________
最近更新
- 下表是根据反应推理得出的影响化学反应的主要因素,其中不合理的是 选项 化学反应事实(或现象) 影响因素 A 氯酸钾加热后
- 在考古学和医学上有着广泛用途,下列有关的说法中正确的是 A.质子数为14 B.中子数为6 C.质量数为8
- 河北省饶阳县的程秀把承包的4亩地入股流转给某民营农业科技有限公司,成为该公司的股东和员工。程秀说:“除了每亩每年保底租金
- 下列属于先天性行为的一组是( ) A猫捉老鼠、老马识途
- .函数f(x)= x2+1的值域为( ) A、 B、 C、 D、
- 黄土高原的地表特征是 A.地势平坦 B.千沟万壑 C.雪山连绵 D.山脉高大,地面崎岖
- 2011年7月19日,西藏和平解放60周年庆祝大会在拉萨召开。西藏自治区党委书记张庆黎说,中共团结带领西藏各族人民共同奋
- 2014年上半年,中央在容忍经济速度适当下滑的前提下,大力推动国内结构性改革。下半年,我国仍将综合运用各种手段对国民经济
- 第五部 《繁星·春水》 文段一 一六八 朦胧的月下—— 长廊静院里。 不是清磐破了岑寂, 便落花的声音, 也听得见了。
- 某航空站安装了一台燃料电池,该电池可同时提供电和水蒸气,所用燃料为氢气,电解质为熔融的碳酸钾。已知电池的总反应为2H2+
- 投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是() A.两枚骰子向上一面的点数之和
- 能正确表示下列反应的离子方程式是()A. 向碳酸氢钙溶液中滴入过量澄清石灰水:Ca2++2HCO3﹣+2OH﹣=CaCO
- 现用氯水来制取含有次氯酸的溶液,既要提高溶液中HClO物质的量浓度,又要降低溶液中HCl浓度,下列措施可以采用的是 A.
- 欲除去Cl2中的少量HCl气体,可选用的试剂是() A.NaOH溶液 B
- 阅读下面的文章,完成8-12题。(15分) 转场的哈萨克 刘斌立 十月,乌尔这拉克决定辞职了。 父亲三天前的
- 对于双氧水和二氧化锰混合制取氧气的实验,下列说法正确的是 A.二氧化锰增加了氧气的含量 B.加快了生成氧气的速
- 除病毒外,绝大多数生物体的结构和功能单位是( ) A、细胞 B、系统 C、组织
- 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点。若抛物线经过图中的三个格点,则
- 在空间中,垂直于同一直线的两条直线的位置关系是()A. 垂直 B. 平行 C. 异面 D. 以上都有可能
- (本小题满分12分) 已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB



