高中 数学
在 中,
中,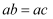 ,
,  为
为 的中点,
的中点, , 则
, 则 面积的最大值为.
面积的最大值为.
 中,
中,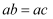 ,
,  为
为 的中点,
的中点, , 则
, 则 面积的最大值为.
面积的最大值为.
已知等差数列  和等比数列
和等比数列  中,
中, 
 和等比数列
和等比数列  中,
中, 
-
(1) 求数列
 和
和  的通项公式;
的通项公式;
-
(2) 如果
 ,写出
,写出 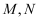 的关系式
的关系式  ,并求
,并求 
已知函数 , .
, .
 , .
, .
-
(1) 求
 的极值;
的极值;
-
(2) 若
 , 且
, 且 , 函数
, 函数 有且仅有两个零点,求a的取值范围.
有且仅有两个零点,求a的取值范围.
已知函数f(x)=2sin(ωx+φ)(ω>0,﹣  )的图象如图所示,直线x=
)的图象如图所示,直线x=  ,x=
,x=  是其两条对称轴.
是其两条对称轴.
 )的图象如图所示,直线x=
)的图象如图所示,直线x=  ,x=
,x=  是其两条对称轴.
是其两条对称轴. 
-
(1) 求函数f(x)的解析式及单调区间;
-
(2) 若f(α)=
 ,且
,且  ,求
,求  的值.
的值.
已知  为一次函数,且
为一次函数,且  则
则  的值为( )
的值为( )
 为一次函数,且
为一次函数,且  则
则  的值为( )
的值为( )
A . 0
B . 1
C . 2
D . 3
某船在A处向正东方向航行xkm后到达B处,然后沿南偏西60°方向航行3km到达C处.若A与C相距  km,则x的值是( )
km,则x的值是( )
 km,则x的值是( )
km,则x的值是( )
A . 3
B .  或2
或2  C . 2
C . 2  D .
D . 
 或2
或2  C . 2
C . 2  D .
D . 
若正方体  的棱长为2,
的棱长为2,  ,
,  ,
,  ,
,  分别为棱
分别为棱  ,
,  ,
,  ,
,  的中点,则四面体
的中点,则四面体  的外接球的半径为( )
的外接球的半径为( )
 的棱长为2,
的棱长为2,  ,
,  ,
,  ,
,  分别为棱
分别为棱  ,
,  ,
,  ,
,  的中点,则四面体
的中点,则四面体  的外接球的半径为( )
的外接球的半径为( )
A .  B . 2
C . 1
D .
B . 2
C . 1
D . 
 B . 2
C . 1
D .
B . 2
C . 1
D . 
已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:
①若m⊥α,m⊂β,则α⊥β;
②若m⊂α,n⊂α,m∥β,n∥β,则α∥β;
③若α∩β=m,n∥m,且n⊄α,n⊄β,则n∥α且n∥β
其中正确命题的序号是.
已知约束条件对应的平面区域 如图所示,其中
如图所示,其中 对应的直线方程分别为:
对应的直线方程分别为: , 若目标函数
, 若目标函数 仅在点
仅在点 处取到最大值,则有( )
处取到最大值,则有( )
A .  B .
B .  C .
C .  D .
D .  或
或
 B .
B .  C .
C .  D .
D .  或
或
已知数列  的通项公式为
的通项公式为  ,则当
,则当 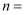 时,
时,  最大;当
最大;当 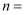 时,
时,  最小.
最小.
 的通项公式为
的通项公式为  ,则当
,则当 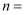 时,
时,  最大;当
最大;当 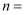 时,
时,  最小.
最小.
函数  的图像大致为( )
的图像大致为( )
 的图像大致为( )
的图像大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在△ABC中,①若 ,则
,则 ②若
②若 ,则
,则 ③若
③若 ,则
,则 ④若
④若 ,则
,则
其中正确结论的个数是( )
 ,则
,则 ②若
②若 ,则
,则 ③若
③若 ,则
,则 ④若
④若 ,则
,则
其中正确结论的个数是( )
A . 1个
B . 2个
C . 3个
D . 4个
已知向量  =(1,2),
=(1,2),  =(x,1).
=(x,1).
 =(1,2),
=(1,2),  =(x,1).
=(x,1).
-
(1) 当
 与2
与2  平行时,求x;
平行时,求x;
-
(2) 当
 与2
与2  垂直时,求x.
垂直时,求x.
已知函数  ,则
,则  .
.
 ,则
,则  .
.
在△ABC中,a,b,c分别是∠A、∠B、∠C的对边长,已知a,b,c成等比数列,且a2-c2=ac-bc.求∠A的大小及  的值.
的值.
 的值.
的值.
玩具厂家设计一款儿童益智玩具,玩具主体是由一矩形托盘和放置在托盘中的L形木块构成,L形木块的水平截面如图1所示,矩形托盘中间有一隔断,隔断的宽为a,隔断上有一开口,开口的长为b,水平截面如图2所示,若木块可以按照图2所示的方式紧贴托盘底部旋转穿过隔断,则 的最小值为.
的最小值为.
 的最小值为.
的最小值为.
.在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 在区间
在区间![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
已知函数![]() 的定义域为集合
的定义域为集合![]() ,
,![]()
(1)求集合![]() ;
;
(2)若全集![]() ,求
,求![]() 及
及![]()
若变量 ![]() ,
, ![]() 满足约束条件
满足约束条件  ,则
,则 ![]() 的最小值为
的最小值为
A.-7 B.-1 C.1 D.2
最近更新
- 用伏安法测量一定值电阻的实验,所用的器材及规格如下: 待测电阻RX(约100Ω) 直流毫安表(量程0-10mA,内阻50
- 世界上信仰人数最多的宗教是( ) A.佛教 B.基督教 C.伊斯兰教
- __________ was it that made him so angry? A. What B.
- 现有200mLNH4HCO3和Na2CO3的混合溶液,加入含a mol氢氧化钠的溶液并加热,恰好反应完全;继续加入含bm
- 31. It was really a wonderful match. If only I__________it a
- 早期的电灯泡,在使用不久后灯泡内部会发黑。开始人们认为是其中的空气引起的,把解决这个问题的思路定在尽可能地把灯泡内部抽成
- 如图所示,两物块A、B套在水平粗糙的CD杆上,并用不可伸长的轻绳连接,整个装置能绕过CD中点的轴OO1转动,已知两物块质
- 下图表示细胞内发生的一系列重大生命活动,据图回答:(1)对于人体来说,在A、B、C、D四项生命活动中,有积极意义的是__
- 以下各项对文章内容的分析,有误的一项是 A、《荷塘月色》一文语言充满诗情画意,具有修辞的美感。如采用许多比喻来表现荷叶、
- 某课外小组的同学,这制备有关物质所设计的下列途径中,正确的是
- (2011年海南高考15题)洋务派要员在筹建轮船招商局时说:“伏查各国通商以来……中国内江外海之利,几被洋人占尽,且海防
- The songs of the birds in the tree sounded , so I
- 绒羽的功能是( )A、保温 B、减轻体重 C、用于飞行 D、减少阻力
- What would you have to do if you ______ to meet him? A. ar
- 下列转化不属于煤或石油的综合利用的是 ( ) A. 将煤干馏制得煤焦油和焦炭 B. 在一定条件下将煤与氢气转化为液
- 我们知道,食物较长时间露置在空气中就会变质,这主要是由于空气中含有 ( )A.氧气 B.
- 下图是某化学反应的微观模型,“ ”、“ ”分别表示不同元素的原子。下列对图示模型理解正确的是( )A.反应前后分子种类
- 3.填入下面一段文字横线处的语句,最恰当的一句是( ) 当今中国既有保护生态环境的指向,又有发展经济的目标。前者
- 如图,在边长为1的正方形网格上有P、A、B、C四点。(1)求证:△PAB∽△PCA (2)求∠APB+∠PBA的度数。
- 假定你是李华,几天前收到美国朋友Jack的Email,他略懂中文,最近听说在中国流行一种名叫“光盘行动”的活动,询问“光



