高中 数学
已知  是递增的等差数列,且满足
是递增的等差数列,且满足  .
.
 是递增的等差数列,且满足
是递增的等差数列,且满足  .
.
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 若
 ,求数列
,求数列  的前
的前  项和
项和  的最小值.
的最小值.
如图,在三棱锥P-ABC中,  ,
,  ,
,  ,
,  ,平面
,平面  平面ABC.
平面ABC.
 ,
,  ,
,  ,
,  ,平面
,平面  平面ABC.
平面ABC. 
-
(1) 求证:
 平面PBC;
平面PBC;
-
(2) 求二面角P-AC-B的余弦值;
-
(3) 求直线BC与平面PAC所成角的正弦值.
已知命题  “曲线
“曲线  表示焦点在
表示焦点在  轴上的椭圆”,命题
轴上的椭圆”,命题  “曲线
“曲线  表示双曲线”.
表示双曲线”.
 “曲线
“曲线  表示焦点在
表示焦点在  轴上的椭圆”,命题
轴上的椭圆”,命题  “曲线
“曲线  表示双曲线”.
表示双曲线”.
-
(1) 若命题
 是真命题,求
是真命题,求  的取值范围;
的取值范围;
-
(2) 若
 是
是  的必要不充分条件,求
的必要不充分条件,求  的取值范围.
的取值范围.
若圆C的半径为1,圆心在第一象限,且与直线4x﹣3y=0和x轴都相切,则该圆的标准方程是
标准的围棋棋盘共19行19列,361个格点,每个格点上可能出现“黑”“白”“空”三种情况,因此有  种不同的情况;而我国北宋学者沈括在他的著作《梦溪笔谈》中,也讨论过这个问题,他分析得出一局围棋不同的变化大约有“连书万字五十二”种,即
种不同的情况;而我国北宋学者沈括在他的著作《梦溪笔谈》中,也讨论过这个问题,他分析得出一局围棋不同的变化大约有“连书万字五十二”种,即  ,下列数据最接近
,下列数据最接近  的是 (
的是 (  )
)
 种不同的情况;而我国北宋学者沈括在他的著作《梦溪笔谈》中,也讨论过这个问题,他分析得出一局围棋不同的变化大约有“连书万字五十二”种,即
种不同的情况;而我国北宋学者沈括在他的著作《梦溪笔谈》中,也讨论过这个问题,他分析得出一局围棋不同的变化大约有“连书万字五十二”种,即  ,下列数据最接近
,下列数据最接近  的是 (
的是 (  )
)
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知直线  ,若
,若  ,则实数
,则实数  ( )
( )
 ,若
,若  ,则实数
,则实数  ( )
( )
A . 0
B . -3
C . 0或3
D . 0或-3
甲、乙两名运动员进行乒乓球单打比赛,根据以往比赛的胜负情况知道,每一局甲胜的概率为  ,乙胜的概率为
,乙胜的概率为  。如果比赛采用“五局三胜”制,求甲以
。如果比赛采用“五局三胜”制,求甲以 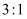 获胜的概率
获胜的概率 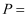
 ,乙胜的概率为
,乙胜的概率为  。如果比赛采用“五局三胜”制,求甲以
。如果比赛采用“五局三胜”制,求甲以 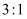 获胜的概率
获胜的概率 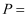
二次函数f(x)满足f(4+x)=f(﹣x),且f(2)=1,f(0)=3,若f(x)在[0,m]上有最小值1,最大值3,则实数m的取值范围是( )
A . [2,4]
B . (0,2]
C . (0,+∞)
D . [2,+∞)
已知函数  .
.
 .
.
-
(1) 当
 时,求函数
时,求函数  的单调区间和极值;
的单调区间和极值;
-
(2) 若
 在
在  上是单调增函数,求实数a的取值范围.
上是单调增函数,求实数a的取值范围.
设方程|ax﹣1|=x的解集为A,若A⊂≠[0,2],则实数a的取值范围是.
-
(1) 计算
 的值;
的值;
-
(2) 已知
 ,求
,求  和
和  的值.
的值.
定义域为R的偶函数f(x)满足对∀x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)至少有6个零点,则a的取值范围是( )
A . (0,  )
B . (0,
)
B . (0,  )
C . (0,
)
C . (0,  )
D . (0,
)
D . (0,  )
)
 )
B . (0,
)
B . (0,  )
C . (0,
)
C . (0,  )
D . (0,
)
D . (0,  )
)
如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是( )

A . 平行
B . 相交
C . 异面
D . 平行和异面
在《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”,已知某“堑堵”的底面是斜边长为2的等腰直角三角形,高为2,则该“堑堵”的表面积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数![]() (m>0且m≠1)
(m>0且m≠1)
(1)求![]() 的定义域,并讨论
的定义域,并讨论![]() 的单调性;
的单调性;
(2)若![]() ,是否存在
,是否存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出此时m的取值范围;若不存在,说明理由.
?若存在,求出此时m的取值范围;若不存在,说明理由.
将杨辉三角中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表.从上往下数,第1次全行的数都为1的是第1行,第2次全行的数都为1的是第3行,…,第![]() 次全行的数都为1的是第 行;第61行中1的个数是 .
次全行的数都为1的是第 行;第61行中1的个数是 .
第1行 1 1
第2行 1 0 1
第3行 1 1 1 1
第4行 1 0 0 0 1
第5行 1 1 0 0 1 1
…… ………………………………………
已知幂函数![]() 的图像过点
的图像过点![]() ,则
,则![]() 的值为
的值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
函数g(x)=2 016x+m图象不过第二象限,则m的取值范围是( )
(A)(-∞,-1] (B)(-∞,-1)
(C)(-∞,-2 016] (D)(-∞,-2 016)
满足条件![]() 的集合
的集合![]() 的个数 .
的个数 .
实数x,y满足x2+y2+xy=1,则x+y的最小值为 .
最近更新
- 有机物A-F存在如下图转变关系,元素分析得知,A分子内含一个氧原子,氢的质量分数为7. 41%,其相对分子质量为108;
- Her leg has been ______ for quite a while, which ,in the mea
- 如图,在xoy直角坐标系中,在第三象限有一平行x轴放置的平行板电容器,板间电压U=1×102V。现有一质量m=1.0×1
- Does he a bus ____? A. take ;home B. takes;home
- 我们的家乡清镇市盛产矿石,有铝都之乡的美誉,也正因为如此,我们这里的汽车超载现象异常突出,公路损坏严重。你认为超载汽车对
- 阅读下面的提示,按要求作文。如果有一种“时空转移心灵交流器”,能把你想说的话传递给古今中外任何一位名人,那么,你将选择哪
- ,往来无白丁。
- (8)已知中,且, 则的形状为: A.锐角三角形 B.钝角三角形 C.等腰直角三角形 D.等边三角形
- 我们要弘扬长征精神,是因为 ( ) A.社会多元化需要弘扬大众文化 B.文化多样化需要
- 下列各组离子中,一定能大量共存的是 ( ) A.加入铝粉只有氢气产生的溶液中:Na+、SO42
- 下图为某植物在生活过程中的两种生理活动,下列有关叙述正确的是()A.植物在白天只进行①生理活动 B.植物在白天只进行②生
- 盐酸和滴有酚酞的氢氧化钠溶液发生反应时,溶液pH变化如下图所示,有关说法不正确的是 A.该实
- 下图中①②③依次为 ()A.生产扩大 供不应求 价格下降 B.生产扩大 价格下降 供不应求
- ______ I know your name? A. May B.Will
- 二次免疫中能直接产生大量抗体的细胞是()
- 有一位同学看到其他同学背上了一种新款式书包,自己也买了同样的书包。这种消费心理是 () A.从众消费心理
- 下面甲图表示洋葱根尖生长点连续分裂的细胞在各个时期细胞核内DNA含量的测定结果;乙图是一组目镜标有5×和16×字样、物镜
- 在研究平抛物体运动的实验中,实验步骤如下: A.让小球多次从 位置上由静止滚下,记下小球平抛过程中经过的一系
- 从2008年9.16起,央行下调一年期人民币贷款基准利率0.27个百分点,同时从9月25日起下调存款类金融机构人民币存款
- 托盘天平左、右两边各放一支质量相等的烧杯,在两只烧杯中均加入等质量、等质量分数的稀盐酸,此时天平保持平衡。然后在左盘烧杯



