高中 数学
 上的单调递增,则 ( )
上的单调递增,则 ( )
 B .
B .  且
且 C . a<0且c=0
D .
C . a<0且c=0
D .  且
且
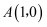 ,
,  ,动点M满足
,动点M满足  ,则动点M的轨迹围成区域的面积为( ).
,则动点M的轨迹围成区域的面积为( ).
 为等差数列,
为等差数列, , 则
, 则
 , 则常数k的值为( )
, 则常数k的值为( )
 在一个周期内的图像如图所示,则此函数的解析式为( )
在一个周期内的图像如图所示,则此函数的解析式为( ) 
 B .
B .  C .
C .  D .
D . 
如图是一个正三棱柱体的三视图,该柱体的体积等于( )
 B .
B . 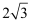 C . 2
D .
C . 2
D . 
 ,则“
,则“  ”是“
”是“  ”的( )
”的( )
 第三象限角,且
第三象限角,且 , 则
, 则 ( )
( )
 B .
B .  C .
C .  D .
D . 
 ,
,  ,若
,若  ,则实数
,则实数  的取值范围是.
的取值范围是.
①M={(x,y)|y=  };②M={(x,y)|y=sinx};③M={(x,y)|y=ex﹣2};
};②M={(x,y)|y=sinx};③M={(x,y)|y=ex﹣2};
④M={(x,y)|y=lgx}.
其中所有“理想集合”的序号是( )
如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.

(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
如图:多面体![]() 中,三角形
中,三角形![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
(1)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]()
![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的角的余弦值.
所成的角的余弦值.

已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期和值域;
的最小正周期和值域;
(Ⅱ)若![]() 为第二象限角,且
为第二象限角,且![]() ,求
,求![]() 的值.
的值.
如图在区域Ω={(x,y)|-2≤x≤2,0≤y≤4}中随机撒900粒豆子,如果落在每个区域的豆子数与这个区域的面积近似成正比,试估计落在图中阴影部分的豆子数.

如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么,小明在这一周中每天所吃水果个数的不同选择方案共有
A.50种 B.51种 C.140种 D.141种
已知![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
![]()
![]() C.
C.![]() D.
D.![]()
判断并证明函数![]() 在(0,2]内的单调性,并求其值域。
在(0,2]内的单调性,并求其值域。
如图,A,C是函数y=![]() 的图像上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则( ).
的图像上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则( ).
A、![]() B、
B、![]()
C、![]() D、
D、![]() 的大小关系不能确定
的大小关系不能确定

(Ⅰ)求曲线
(Ⅱ)已知曲线
- ......
- 据国家发改委、国家统计局调查显示,2007年10月,全国70个大中城市房屋销售价格同比上涨9.5%。小张害怕房价再上涨,
- 现有以下几种措施:①对燃烧煤时产生的尾气进行除硫处理 ②少用原煤作燃料 ③燃煤时鼓入足量空气 ④开发清洁能源 其中
- 依次填入下列各句横线处的词语,恰当的一组是( ) ①海外华侨华人纷纷发表声明或谈话,坚决拥护 《反分
- 验证淀粉水解可生成还原性糖,进行如下实验,在该实验中,操作步骤排序正确的是( )①取少量的淀粉加适量水制成溶液
- 各国对制造、贩卖假币都进行坚决打击,但仍有不法分子制造和销售假币,从经济学角度看,不法分子制造和销售假币原因是
- 根据拼音写出汉字(3分)漫步汤山公园,举目西望,惊涛拍案,一座座zhàn( )桥向远处延伸。尽那边,杭州湾跨海大桥
- 在中国古代传统思想中,有着众多的学派。儒、墨、道、法是其中最著名,也是影响最大的四个学派。自古至今,四大学派一直受到人们
- ——What do you do atthe weekend, Jim? ——I prefer________
- 材料一 家住如皋郊区的小李2006年大学毕业后应聘了许多岗位,但他不是嫌累、嫌工资少,就是嫌地位低,嫌与他那个适用面很
- For breakfast he only drinks juice from fresh fruit ___ on h
- 平面上满足约束条件的点形成的区域为,则区域的面积为 ________;设区域关于直线对称的区域为,则区域和区域中距离 最
- 22.阅读下面的材料,根据要求作文。 日常新闻正在不断加剧人们对科技进步的担忧:优步的出现可能令出租车司机失业,而自动驾
- 下面两个句子都写到“虚伪”。前一句直接表述,言简意赅;后一句连续类比,形象生动。请在“友谊”“勇敢”信任”中任选一个词语
- 设集合U=R,A={x|<2x<4},B={x|lgx>0},则 A. B.C.
- 在2A(g)+B(g) 3C(g)+4D(g)中,下列情况能够降低该反应速率的是 A.升高温度 B.减小压强
- 若两个相似三角形的相似比是1:4,则它们的周长是( ) (A)1:2 (B)1:4 (C)1:16
- 写作 在下面两题中,任选一题,按要求作文。 (一)请以 “是你教会我 (如:自尊、坚强、宽容、微笑……)”为
- 下列各组词语中相同字的读音,全都与所给注音相同的一组是 ( ) A.拗(ǎo) 拗断 拗口
- 下列物质中核磁共振氢谱中只有一个峰的物质是 A. 乙烷 B. 丙烷 C. 正丁烷



