高中 数学
已知函数 的部分图像如图所示,设函数
的部分图像如图所示,设函数 , 则
, 则 的值域为.
的值域为.
 的部分图像如图所示,设函数
的部分图像如图所示,设函数 , 则
, 则 的值域为.
的值域为.
若圆锥的侧面积是底面积的3倍,则其母线与底面角的大小为(结果用反三角函数值表示).
试用集合A,B的交集、并集、补集表示图中阴影部分所表示的集合( )

A . ∁UB
B . A∩(∁UB)
C . A∪(∁UB)
D . ∁U(A∩B)
关于x的不等式  的解集为( )
的解集为( )
 的解集为( )
的解集为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知直线  与直线
与直线  平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
 与直线
与直线  平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
A .  B . 1
C .
B . 1
C .  D .
D . 
 B . 1
C .
B . 1
C .  D .
D . 
17世纪法国数学家费马在《平面与立体轨迹引论》中证明,方程  (k>0,k≠1,a≠0)表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P向长轴AB(异于A , B两点)引垂线,垂足为Q , 则
(k>0,k≠1,a≠0)表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P向长轴AB(异于A , B两点)引垂线,垂足为Q , 则  为常数.据此推断,此常数的值为( )
为常数.据此推断,此常数的值为( )
 (k>0,k≠1,a≠0)表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P向长轴AB(异于A , B两点)引垂线,垂足为Q , 则
(k>0,k≠1,a≠0)表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P向长轴AB(异于A , B两点)引垂线,垂足为Q , 则  为常数.据此推断,此常数的值为( )
为常数.据此推断,此常数的值为( )
A . 椭圆的离心率
B . 椭圆离心率的平方
C . 短轴长与长轴长的比
D . 短轴长与长轴长比的平方
已知向量 ,
,  的夹角为
的夹角为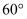 ,
,  ,
,  , 则
, 则 ( )
( )
 ,
,  的夹角为
的夹角为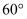 ,
,  ,
,  , 则
, 则 ( )
( )
A . 1
B . 2
C . 3
D . 4
在 中,角
中,角 所对的边分别为
所对的边分别为 .
.
 中,角
中,角 所对的边分别为
所对的边分别为 .
.
-
(1) 若
 , 求
, 求 的值;
的值;
-
(2) 若
 , 求
, 求 的值;
的值;
-
(3) 若
 , 且
, 且 , 三角形的面积
, 三角形的面积 , 求边
, 求边 的值.
的值.
函数  的定义域是( )
的定义域是( )
 的定义域是( )
的定义域是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知a=21.3 , b=40.7 , c=ln6,则a,b,c的大小关系为( )
A . a<b<c
B . b<c<a
C . c<a<b
D . c<b<a
若f(cosx)=cos2x,f(sin15°)=( )
A .  B . -
B . -  C .
C .  D . -
D . - 
 B . -
B . -  C .
C .  D . -
D . - 
若实数x、y满足 =1,则x2+2y2有( )
=1,则x2+2y2有( )
 =1,则x2+2y2有( )
=1,则x2+2y2有( )
A . 最大值3+2
B . 最小值3+2 C . 最大值6
D . 最小值6
C . 最大值6
D . 最小值6
 C . 最大值6
D . 最小值6
C . 最大值6
D . 最小值6
有5个男生和3个女生,从中选出5人担任5门不同学科的课代表,分别求符合下列条件的选法数:(结果用数字)
-
(1) 有女生但人数必须少于男生;
-
(2) 某女生一定要担任语文课代表;
-
(3) 某男生必须包括在内,但不担任数学课代表;
-
(4) 选取3名男生和2名女生分别担任5门不同学科的课代表,但数学课代表必须由男生担任,语文课代表必须由女生担任.
甲、乙两支足球队进行比赛,根据赛前的数据分析,甲队赢球的概率为0.55,乙队赢球的概率为0.2,则两支球队踢成平局的概率为.
计算:
-
(1)
 ;
;
-
(2)
 .
.
已知函数  是定义在
是定义在  上的减函数,则实数
上的减函数,则实数  的取值范围为( )
的取值范围为( )
 是定义在
是定义在  上的减函数,则实数
上的减函数,则实数  的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数 , 下列说法中正确的是( )
, 下列说法中正确的是( )
 , 下列说法中正确的是( )
, 下列说法中正确的是( )
A . 若 的定义域为R,则
的定义域为R,则 B . 若
B . 若 的值域为R,则
的值域为R,则 或
或 C . 若
C . 若 , 则
, 则 的单调减区间为
的单调减区间为 D . 若
D . 若 在
在 上单调递减,则
上单调递减,则
 的定义域为R,则
的定义域为R,则 B . 若
B . 若 的值域为R,则
的值域为R,则 或
或 C . 若
C . 若 , 则
, 则 的单调减区间为
的单调减区间为 D . 若
D . 若 在
在 上单调递减,则
上单调递减,则
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
|
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,y=a+bx与y=c+d![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:

若三点A(1,5,-2),B(2,4,1),C(a,3,b+2)在同一条直线上,则a=________,b=________.
设函数f(x)=tan![]() .
.
(1)求函数f(x)的最小正周期,图象的对称中心;
(2)作出函数f(x)在一个周期内的简图.
最近更新
- “棕子香香厨房,艾叶香,香满堂”。这句民谣描写的是我国哪一传统节日( ) A.端午节 B.中秋
- (2013唐山一中检测)粗细均匀的电阻丝围成图所示的线框,置于正方形有界匀强磁场中,磁感强度为B,方向垂直于线框平面,图
- 下列说法中,正确的是 A.元素
- p{font-size:10.5pt;line-height:150%;margin:0;padding:0;}td{f
- 如图所示,下列说法中正确的是( ) A.甲是近视眼,用乙模型矫正B.甲是远视眼,用乙模型矫正 C.甲是近视眼,用丙
- In my opinion,_____ shouldn't be any doubt that Chinawill be
- 填入下面横线上的句子,与上文衔接最恰当的一项是( ) 崇山峻岭,比起人来,总是高大雄伟的,人站在它面前不过是颗芝麻粒儿。
- 已知函数在区间上有最小值,则实数的取值范围是 A. B. C. D.
- 科学家用小鼠作实验材料,完成生长激素和胰岛素相关实验,结果如下图所示,相关分析正确的是 ( )A.增大生长激素
- 关于的方程的解是正数,则的取值范围是 .
- 1937年,日本发动侵略中国的事件是 A、九一八事变 B、七七事变 C、一二·九运动 D、南京
- 生活中处处有化学. (1)人类六大营养素中,能供给人体能量的有油脂、蛋白质和.青少年缺.(填写元素符号)会患佝偻病和发育
- 新中国成立60年以来,新疆自治区始终坚持把民族教育摆在优先发展的战略地位,着力提高少数民族整体素质,培养大量高素质的具有
- 下列各句没有语病的一项是( ) A.尽管警方表示奥姆真理教负责人坦白该教手中已经没有了毒气,但是谁也不敢保证这一坦
- 责任产生于: A.社会关系之中的相互承诺 B.利益双方的相互承诺 C.父母子女之间的相互承诺
- 据新华社电:2011年日本大地震后,富士山等13座活火山活动加剧,应密切关注。据此回答9~10题。9.此火山口喷出的大量
- 世界上国家数目最多的大洲是() A、非洲 B、亚洲 C、欧洲
- 甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(
- 下列词语中加点的字,每对读音都不相同的一组是( ) A.复辟/开天辟地 间或/间不容发 风靡/靡靡之音
- 在短周期元素中,原子最外电子层只有1个或2个电子的元素是( ) A.金属元素



