高中 数学
已知集合A={1,2},B={x|3x﹣a=0},若B⊆A,则实数的a值是.
已知集合 ,
,  , 则
, 则 ( )
( )
 ,
,  , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D . {0}
D . {0}
 B .
B .  C .
C .  D . {0}
D . {0}
设  ,向量
,向量  ,
,  ,若
,若  ,则
,则  等于( )
等于( )
 ,向量
,向量  ,
,  ,若
,若  ,则
,则  等于( )
等于( )
A .  B .
B .  C . -4
D . 4
C . -4
D . 4
 B .
B .  C . -4
D . 4
C . -4
D . 4
已知函数 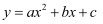 ,如果
,如果  且
且  ,则它的图象可能是( )
,则它的图象可能是( )
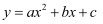 ,如果
,如果  且
且  ,则它的图象可能是( )
,则它的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知某圆柱的底面周长为12,高为2,矩形  是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为( )
是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为( )
 是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为( )
是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为( ) 
A .  B .
B . 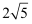 C . 3
D . 2
C . 3
D . 2
 B .
B . 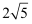 C . 3
D . 2
C . 3
D . 2
已知  ,则cos2α﹣sin2α=.
,则cos2α﹣sin2α=.
 ,则cos2α﹣sin2α=.
,则cos2α﹣sin2α=.
已知函数 , 若方程
, 若方程 有且仅有三个实数解,则实数
有且仅有三个实数解,则实数 的取值范围为( )
的取值范围为( )
 , 若方程
, 若方程 有且仅有三个实数解,则实数
有且仅有三个实数解,则实数 的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若关于  的不等式
的不等式  恒成立,则实数
恒成立,则实数  的取值范围是( )
的取值范围是( )
 的不等式
的不等式  恒成立,则实数
恒成立,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  是偶函数,
是偶函数,  是奇函数,它们的定义域是
是奇函数,它们的定义域是  ,且它们在
,且它们在  的图象如图所示,则不等式
的图象如图所示,则不等式  的解集为( )
的解集为( )
 是偶函数,
是偶函数,  是奇函数,它们的定义域是
是奇函数,它们的定义域是  ,且它们在
,且它们在  的图象如图所示,则不等式
的图象如图所示,则不等式  的解集为( )
的解集为( )
A . 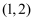 B .
B .  C .
C .  D .
D . 
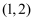 B .
B .  C .
C .  D .
D . 
满足{1,2,3}⊆B⊆{1,2,3,4,5}的集合B有个.
把Rt△ABC沿斜边上的高CD折起使平面ADC⊥平面BDC,如图所示,互相垂直的平面有 对.

已知直线l1:x+(1+m)y+m﹣2=0与直线l2:mx+2y+8=0平行,则经过点A(3,2)且与直线l1垂直的直线方程为
如图是函数  的导函数
的导函数  的图象,给出下列命题:
的图象,给出下列命题:
 的导函数
的导函数  的图象,给出下列命题:
的图象,给出下列命题: ①-2是函数  的极值点;②1不是函数
的极值点;②1不是函数  的极值点;③
的极值点;③  在
在 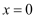 处切线的斜率小于零;④
处切线的斜率小于零;④  在区间
在区间  上单调递增.其中正确命题的序号是( )
上单调递增.其中正确命题的序号是( )

A . ①②④
B . ①②③
C . ②③④
D . ①②
已知  ,
,  ,且
,且  ,其中
,其中  为坐标原点,则
为坐标原点,则  点坐标为( )
点坐标为( )
 ,
,  ,且
,且  ,其中
,其中  为坐标原点,则
为坐标原点,则  点坐标为( )
点坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若|a|=2sin15°,|b|=4cos15°,a与b的夹角为30°,则a·b的值是( )
A .  B .
B .  C . 2
C . 2  D .
D . 
 B .
B .  C . 2
C . 2  D .
D . 
已知函数![]() 在点
在点![]() 的切线方程为
的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,求证:
,求证:![]() 在
在![]() 上恒成立;
上恒成立;
(Ⅲ)已知![]() ,求证:
,求证:![]() .
.
选修4—4:坐标系与参数方程。
已知曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (t为参数)若直线
(t为参数)若直线![]() 与曲线C相切。 求:a的值。
与曲线C相切。 求:a的值。
如图,点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.

如图是一容量为100的样本的质量的频率分布直方图,则由图可估计样本质量的中位数为( )

A.11 B.11.5
C.12 D.12.5
已知方程x2+(a﹣2)x+5﹣a=0的两个根均大于2,则实数a的取值范围是 .
最近更新
- 某非金属单质A经如下图所示的过程转化为含氧酸D,;已知D为强酸,请回答: (1)若A常温下为淡黄色固体,B是有刺激性气味
- 18世纪的英国,只有国王和议会才能授予公司特许……,但是,19世纪中叶以后,国家对企业的设立逐渐摈弃特权主义,企业的设立
- (2010·陕西省宝鸡市高三教学质量检测三) 18.She is lucky to have found a job s
- (13分)在75℃左右,用HgSO4做催化剂,乙炔可水化为乙醛,但HgSO4遇到某些特定物质常会发生催化剂中毒而失去催化
- 图一是某同学在公园里做完调查之后,根据所学的生物学知识绘制的一幅结构示意图,根据你自己的相关知识解答他的一些疑难:(1)
- 设NA为阿伏加德罗常数的值,下列说法正确的是( ) A.1 mol NaHSO4熔融或溶于水时电离出的离子总数均为
- 如图为元素周期表前四周期的一部分, 下列有关R、W、X、Y、Z 这5种元素的叙述中,正确的是 A.常压下5种元素的单质中
- 下列情况对空气质量指标不会产生影响的是( ) A、焚烧垃圾 B、用煤和石油产品作燃料C、太阳能的利用 D、汽车排
- 7.细菌很难生存在蜂蜜中,这是因为:() A.蜂蜜中含有天然的抗生素 B.蜂蜜中含有溶菌酶 C.蜂蜜中含有限制性内切酶
- 【原创】已知。当时,=7,那么,当=3时,= ( )A.B.C.D.
- 我国各少数民族都按照本民族的传统习俗欢度节日,如:藏族的藏历新年、“雪顿节”,回族、维吾尔等民族的“开斋节”、“古尔邦节
- 将一定量的铁粉放入含AgNO3和Zn(NO3)2的混合溶液里,搅拌,使其充分反应后过滤,滤渣中加入稀盐酸,有气泡产生,则
- 19世纪中后期,西方列强通过殖民扩张把广大亚、非、拉美地区沦为自己的殖民地或半殖民地。下列国家中,通过改革摆脱民族危机、
- 关于商品、货币和一般等价物三者之间关系描述正确的是 A.货币是一种特殊的商品,货币的本质是商品 B.一般等价物能表现其他
- 下列事件发生的先后顺序是( ) (1)九一八事变 (2)七七事变 (
- 下列词语中,没有错别字的一组是 A.雏形首屈一指消声匿迹智者千虑,必有一失 B.宣泄茅塞顿开相濡以沫坐收鱼人之利 C.证
- .......
- 罗斯福新政产生的效果有( ) ①使美国经济逐渐走出低谷 ②消除了资本主义社会的基本矛盾③遏制了美国法西斯主
- 30.基因型为AaBbCcDD的生物个体自交(按自由组合定律遗传),则其后代中基因型和表现型分别有 A.27种、8种
- ......



