高中 数学
设命题  对任意
对任意  ,不等式
,不等式  恒成立;命题q:存在
恒成立;命题q:存在  ,使得不等式
,使得不等式  成立.
成立.
 对任意
对任意  ,不等式
,不等式  恒成立;命题q:存在
恒成立;命题q:存在  ,使得不等式
,使得不等式  成立.
成立.
-
(1) 若p为真命题,求实数m的取值范围;
-
(2) 若命题p、q有且只有一个是真命题,求实数m的取值范围.
2019年初,某零售业巨头入驻石家庄市.为确定开设分店的个数,该公司对已开设分店的其他地区的数据得到如下表格.记  表示在各区开设的分店个数,
表示在各区开设的分店个数,  表示这
表示这  个分店的年收入之和.
个分店的年收入之和.
 表示在各区开设的分店个数,
表示在各区开设的分店个数,  表示这
表示这  个分店的年收入之和.
个分店的年收入之和. | | 2 | 3 | 4 | 5 | 6 |
| | 2.5 | 3 | 4 | 4.5 | 6 |
-
(1) 求
 关于
关于  的线性回归方程;
的线性回归方程;
-
(2) 假设该公司获得的总年利润
 (百万元)与
(百万元)与  之间满足
之间满足  试结合(1)中的线性回归方程,估计该公司在石家庄市需要开设多少分店,才能使得平均每个分店的年利润最大?
试结合(1)中的线性回归方程,估计该公司在石家庄市需要开设多少分店,才能使得平均每个分店的年利润最大? (注:
 ,
,  ,)参考数据
,)参考数据 
将1,2,3,4,5,6这6个数填入如图所示的3行2列表格中,要求表格每一行数字之和均相等,则可组成不同表格的个数为( )

A . 8
B . 24
C . 48
D . 64
设等差数列  的前n项和为Sn , 若S3=9,S6=36,则a7+a8+a9=( )
的前n项和为Sn , 若S3=9,S6=36,则a7+a8+a9=( )
 的前n项和为Sn , 若S3=9,S6=36,则a7+a8+a9=( )
的前n项和为Sn , 若S3=9,S6=36,则a7+a8+a9=( )
A . 63
B . 45
C . 43
D . 27
已知  是定义在
是定义在  上的函数
上的函数  的导函数,且
的导函数,且  ,当
,当 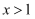 时,
时,  恒成立,则下列判断正确的是( )
恒成立,则下列判断正确的是( )
 是定义在
是定义在  上的函数
上的函数  的导函数,且
的导函数,且  ,当
,当 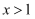 时,
时,  恒成立,则下列判断正确的是( )
恒成立,则下列判断正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知定义在R上的偶函数满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;
②x=﹣4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]单调递增;
④若方程f(x)=m在[﹣6,﹣2]上的两根为x1 , x2 , 则x1+x2=﹣8.
上述命题中所有正确命题的序号为.
设△ABC的内角A,B,C所对的边分别为a,b,c,在△ABC中,若  ,则△ABC一定是( )
,则△ABC一定是( )
 ,则△ABC一定是( )
,则△ABC一定是( )
A . 等腰三角形
B . 直角三角形
C . 等腰直角三角形
D . 等腰三角形或直角三角形
若  ,则
,则  .
.
 ,则
,则  .
.
已知 且
且 , 函数
, 函数 与函数
与函数 在同一个坐标系中的图象可能是( )
在同一个坐标系中的图象可能是( )
 且
且 , 函数
, 函数 与函数
与函数 在同一个坐标系中的图象可能是( )
在同一个坐标系中的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数 的图象关于( )
的图象关于( )
 的图象关于( )
的图象关于( )
A .  轴对称
B .
轴对称
B .  轴对称
C . 坐标原点对称
D . 直线
轴对称
C . 坐标原点对称
D . 直线 轴对称
轴对称
 轴对称
B .
轴对称
B .  轴对称
C . 坐标原点对称
D . 直线
轴对称
C . 坐标原点对称
D . 直线 轴对称
轴对称
已知数列  的前
的前  项和
项和  ,设
,设  ,
,  为数列
为数列  的前n项和,若对任意的
的前n项和,若对任意的  ,不等式
,不等式  恒成立,则实数
恒成立,则实数  的取值范围为( )
的取值范围为( )
 的前
的前  项和
项和  ,设
,设  ,
,  为数列
为数列  的前n项和,若对任意的
的前n项和,若对任意的  ,不等式
,不等式  恒成立,则实数
恒成立,则实数  的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
等比数列  的前n项和为
的前n项和为  ,已知
,已知  ,则
,则  ( )
( )
 的前n项和为
的前n项和为  ,已知
,已知  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图所示,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为(x,0).

-
(1) 求函数S=f(x)的解析式;
-
(2) 解不等式f(x)<14.
下图是国家统计局发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图,其中上面折线是同比涨跌幅情况折线图,下面折线是环比涨跌幅情况折线图,(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论不正确的是( )

A . 2018年3月至2019年3月全国居民消费价格同比均上涨
B . 2018年3月至2019年3月全国居民消费价格环比有涨有跌
C . 2019年3月全国居民消费价格同比涨幅最大
D . 2019年3月全国居民消费价格环比变化最快
已知函数  在区间[1,2]上单调递增,则
在区间[1,2]上单调递增,则  的取值范围是( )
的取值范围是( )
 在区间[1,2]上单调递增,则
在区间[1,2]上单调递增,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知:sin230°+sin290°+sin2150°=  ;
;
 ;
;sin25°+sin265°+sin2125°=  ;
;
sin212°+sin272°+sin2132°=  ;
;
通过观察上述两等式的规律,请你写出一般性的命题,并给予的证明.
如图,正三角形ABE与菱形ABCD所在的平面互相垂直,AB=2,∠ABC=60°,M是AB的中点.

(I)求证:EM⊥AD;
(II)求二面角A﹣BE﹣C的余弦值;
(III)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为45°,若存在,求出  的值;若不存在,说明理由.
的值;若不存在,说明理由.
若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 .
,则此数列的通项公式为 .
已知函数f(x)=x2﹣(2a+1)x+alnx.
(1)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当![]() a>0时,求函数f(x)的单调区间;
a>0时,求函数f(x)的单调区间;
(3)若对任意![]() 时,恒有ma﹣f(x)<1成立,求实数m的取值范围.
时,恒有ma﹣f(x)<1成立,求实数m的取值范围.
定义 ,已知函数
,已知函数 ,
, ,
, ,则
,则 的取值范围是__________,若
的取值范围是__________,若 有四个不同的实根,则
有四个不同的实根,则 的取值范围是__________.
的取值范围是__________.
最近更新
- —Look! Jane has ______ tense expression on her face. —S
- 17.下表反映了19世纪末20世纪初中国出口商品的情况。对下表解读正确的是()分类年份总量(吨)商品分类比重(%) 原料
- “往者,忧世之士亦鼓吹工业主义,以挽救时艰,而无效也。”后来他们认为“产业革命,今也其时矣”。导致上述变化的主要原因是
- (08年韶关市模拟)(12分)如图(甲)所示,在利用重物自由下落验证机械能守恒定律的实验中,某实验小组打出了三条纸带,但
- 葡萄糖在机体内彻底氧化和在体外燃烧的相同点是 ①都是葡萄糖中的碳和氢气与空气中的氧直接化合; ②能量都是逐步释放出来的;
- I usually take walks after supper. Buttoday I want to do __
- 2015年12月25日,山东省政府削减省级行政审批事项54项,涉及教育、医疗卫生、海洋渔业等领域。这意味着政府将 A.
- 0下列四组生物中,都属于真核生物的一组是:A.噬菌体和根霉 B.细菌和草履虫 C.蓝藻和酵母菌 D.衣藻和变形虫
- The car is expensive he cannotbuy it. A.too
- 5.下列各组加横线的词,词义相同的一项是( ) A.夫何使我至于此极也 而余亦悔其随之而不得极夫游
- 下列实验或现象中,可证明胶体粒子带电荷的是() A.电泳 B.丁达尔效应
- 如图,将45°直角三角板和30°直角三角板拼在一起,其中45°直角三角板的斜边与30°直角三角板的30°角所对的直角边重
- 读东西半球图,完成下列内容(1)写出下列字母所代表的大洲和大洋的名称 A B
- (4分)某兴趣小组进行粗盐提纯并配制NaCl溶液,请回答下列问题:(1)操作①、②、③依次为下图中的(填字母)
- 下列关于生长素的叙述,不正确的是() A.在植物体内可以进行极性运输和非极性运输 B.在植物体中含量很少,主要分布在生长
- 下列句子的表述有误的两项是( )( ) A.小说开始介绍葛朗台概况时,作者用漫画式的手法,从语言和行动上对葛
- Thomas Alva Edison didn’t “invent” the light bulb (灯泡), but
- 如图2-3-3所示,长为L的匀质链条,对称地悬挂在光滑的小滑轮上.若链条因受到微扰而滑动,求链条刚脱离滑轮时的速度. 图
- 中国歌手刘欢和英国歌手莎拉?布莱曼在2008年北京奥运会开幕式上演唱主题歌《我和你》,引起网民热议。“难道中国没有自己拿
- 若打点计时器采用50 Hz的交流电供电,并且每打5个点选一个计数点,那么,相邻计数点之间的时间间隔为_____.



