高中 数学
下列各组函数,在同一直角坐标系中  与
与  相同的一组是
相同的一组是 

 与
与  相同的一组是
相同的一组是 

A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
从1,3,5,7,9中任取3个不同的数字分别作为  ,则
,则  的概率是.
的概率是.
 ,则
,则  的概率是.
的概率是.
若曲线  和
和  上分别存在点
上分别存在点  ,使得
,使得 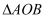 是以原点
是以原点  为直角顶点的直角三角形,
为直角顶点的直角三角形,  交
交  轴于点
轴于点  ,且
,且  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
 和
和  上分别存在点
上分别存在点  ,使得
,使得 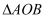 是以原点
是以原点  为直角顶点的直角三角形,
为直角顶点的直角三角形,  交
交  轴于点
轴于点  ,且
,且  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量  .若
.若  ,则x的值为( )
,则x的值为( )
 .若
.若  ,则x的值为( )
,则x的值为( )
A . -2
B . 2
C . 3
D . -3
在下列各图中,每个图的两个变量具有相关关系的图是 ( )

A . (1)(2)
B . (1)(3)
C . (2)(4)
D . (2)(3)
已知 的展开式中,
的展开式中, 项的系数是( )
项的系数是( )
 的展开式中,
的展开式中, 项的系数是( )
项的系数是( )
A . 10
B . -10
C . 40
D . -40
若 则角
则角 的终边落在直线( )上
的终边落在直线( )上
 则角
则角 的终边落在直线( )上
的终边落在直线( )上
A . 24x-7y=0
B . 24x+7y=0
C . 7x+24y=0
D . 7x-24y=0
新能源汽车的核心部件是动力电池,电池占了新能源整车成本的大头,而其中的原材料碳酸锂又是电池的主要成分.从2020年底开始,碳酸锂的价格一路水涨船高,下表是2022年某企业的前5个月碳酸锂的价格与月份的统计数据:
月份代码 | 1 | 2 | 3 | 4 | 5 |
碳酸锂价格 | 0.5 | 0.6 | 1 |
| 1.5 |
根据表中数据,得出y关于x的经验回归方程为 , 根据数据计算出在样本点
, 根据数据计算出在样本点 处的残差为
处的残差为 , 则表中
, 则表中 .
.
命题“  ,
,  ”的否定是( )
”的否定是( )
 ,
,  ”的否定是( )
”的否定是( )
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
已知直线ax﹣y+2a=0和(2a﹣1)x+ay+a=0互相垂直,则a=.
点在圆 上移动时,它与定点
上移动时,它与定点 连线的中点的轨迹方程是( )
连线的中点的轨迹方程是( )
 上移动时,它与定点
上移动时,它与定点 连线的中点的轨迹方程是( )
连线的中点的轨迹方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在空间直角坐标系O﹣xyz中,设点M是点N(2,﹣3,5)关于坐标平面xoz的对称点,则线段MN的长度等于.
以点(3,﹣1)为圆心且与直线3x+4y=0相切的圆的方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
阅读右边的程序框图,运行相应的程序,则输出 i 的值为 ( )
A . 3
B . 4
C . 5
D . 6
已知直线  ,圆
,圆  .
.
 ,圆
,圆  .
.
-
(1) 求直线
 被圆截得的弦长;
被圆截得的弦长;
-
(2) 在直线
 取一点
取一点  ,设Q为圆C上的点,求
,设Q为圆C上的点,求  的取值范围.
的取值范围.
学校艺术节对同一类的  ,
,  ,
,  ,
,  四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
 ,
,  ,
,  ,
,  四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是  或
或  作品获得一等奖”;
作品获得一等奖”;
乙说:“  作品获得一等奖”;
作品获得一等奖”;
丙说:“  ,
,  两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是  作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是.
(2009年龙岩市普通高中毕业班单科质量检查)已知![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
 在四棱锥
在四棱锥![]() 中,
中,![]() 平面
平面![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
在等差数列![]() 中,
中,![]() ,则此数列的前13项的和等于( )
,则此数列的前13项的和等于( )
A.13 B.26 C.8 D.16
不等式 的解集是( )
的解集是( )
A.
B.
C.
D. 或
或
A.
B.
C.
D.
最近更新
- 关于水的离子积常数Kw与水的电离平衡常数Kc的叙述中,正确的是 ( ) A.Kw和Kc都随温度
- 透视“姚明现象”,体育明星赚钱速度最快,从心理经济学来看,人只为自己喜欢的人买单。2.26米的身高、幽默的谈吐、良好的潜
- 2008年8月8日,北京奥运会火炬在北京正式完成奥运任务。下列图片中,为2008北京奥运会火炬的是
- 已知集合,则集合=( ) (A) (B) (C) (D)
- 下列有关酸的说法错误的是() A. 浓硫酸具有吸水性,浓盐酸具有挥发性 B. 稀盐酸和稀硫酸都可用于金属除锈 C. 稀盐
- 学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示.已知每个菱形图案
- 人们之所以要尊重生命,是因为① 它是地球上最宝贵的东西② 只有人类的生命才需要尊重③ 它是珍贵的④ 人类是自然界的一部分
- 右图为DNA分子结构示意图,对该图的描述正确的是( )A.②和③相间排列,构成了DNA分子的基本骨架 B.④的名称
- 两实验小组使用相同规格的元件,按图3-4-17电路进行测量.他们将滑动变阻器的滑片P分别置于a、b、c、d、e五个间距相
- 下列物质属于同系物的是 A.CH3CH2CH2OH与CH3OH
- 阅读下列短文并按要求回答问题(共3小题,满分7分) In China, more and more middle sch
- 下列关于声现象的说法正确的是()A. 声音在15℃的空气中的传播速度是340m/s B. 宇航员能够进行交流,所以真空能
- 下列关于动物体的内环境和稳态的叙述不正确的是 A.葡萄糖、生物激素、抗体都属于人体内环境的成分 B.内环境稳态若不能维持
- As a basketball player, you should always keep in mindthat i
- 下表是分析豌豆的两对基因遗传情况所得到的F2基因型结果(非等位基因位于非同源染色体上),表中列出部分基因型,有的以数字表
- 染色体、DNA、基因三者关系密切,下列叙述中不正确的是 ( ) A.每个染色体一般含有一个DNA分子,每个D
- 如图,、分别是、上一点,,与互余,.试说明
- 绿色化学的核心是反应过程的绿色化,即要求原料物质中的所有原子完全被利用且全部转入期望的产品中,下列过程不符合这一思想的的
- 下列属于化学变化的是( ) A.石蜡融化 B.衣服晾干 C.酒精挥发 D.食物腐败
- 如图所示,在垂直于纸面的范围足够大的匀强磁场中,有一个矩形线圈abcd,线圈平面与磁场垂直,O1O2是线圈的对称轴,应





