高中 数学
已知函数f(x)=ax3+3x2+2,若f′(﹣1)=4,则a的值等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若平面向量  、
、  满足
满足  ,
,  .
.
 、
、  满足
满足  ,
,  .
.
-
(1) 若
 .求
.求  与
与  的夹角;
的夹角;
-
(2) 若
 ,求
,求  的坐标.
的坐标.
若直线y=k(x+2)上存在点(x,y)∈{(x,y)|x﹣y≥0,x+y≤1,y≥﹣1},则实数k的取值区间为.
已知函数  和
和  的图像如图所示,则不等式
的图像如图所示,则不等式  的解集是
的解集是
 和
和  的图像如图所示,则不等式
的图像如图所示,则不等式  的解集是
的解集是 
已知向量 满足
满足 .
.
 满足
满足 .
.
-
(1) 求
 ;
;
-
(2) 若
 , 求实数
, 求实数 的值.
的值.
设函数  ,
,  ,若存在
,若存在  、
、  使得
使得  成立,则
成立,则  的最小值为1时,实数
的最小值为1时,实数  .
.
 ,
,  ,若存在
,若存在  、
、  使得
使得  成立,则
成立,则  的最小值为1时,实数
的最小值为1时,实数  .
.
已知全集  ,集合
,集合  ,集合
,集合  ,则
,则  为 ( )
为 ( )
 ,集合
,集合  ,集合
,集合  ,则
,则  为 ( )
为 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数f(x)在R上存在导数f′(x),∀x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(2﹣m)+f(﹣m)﹣m2+2m﹣2≥0,则实数m的取值范围为( )
A . [﹣1,1]
B . [1,+∞)
C . [2,+∞)
D . (﹣∞,﹣2]∪[2,+∞)
若  ,则
,则  的最小值为( )
的最小值为( )
 ,则
,则  的最小值为( )
的最小值为( )
A . 1
B . 2
C .  D . 4
D . 4
 D . 4
D . 4
设函数f(x)=lnx+x2﹣ax(a∈R).
(Ⅰ)当a=3时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个极值点x1 , x2 , 且x1∈(0,1],求证:f(x1)﹣f(x2)≥﹣ +ln2;
+ln2;
(Ⅲ)设g(x)=f(x)+2ln , 对于任意a∈(2,4),总存在
, 对于任意a∈(2,4),总存在 , 使g(x)>k(4﹣a2)成立,求实数k的取值范围.
, 使g(x)>k(4﹣a2)成立,求实数k的取值范围.
不等式  的解集为( )
的解集为( )
 的解集为( )
的解集为( )
A . (-4,1)
B . (-1,4)
C . (-∞,-4)∪(1,+∞)
D . (-∞,-1)∪(4,+∞)
函数  的定义域为( ).
的定义域为( ).
 的定义域为( ).
的定义域为( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知三棱锥  的体积为
的体积为 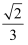 ,且
,且  ,
,  ,
,  ,则三棱锥
,则三棱锥  的表面积为( )
的表面积为( )
 的体积为
的体积为 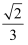 ,且
,且  ,
,  ,
,  ,则三棱锥
,则三棱锥  的表面积为( )
的表面积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,  ,则C的实轴长为( )
,则C的实轴长为( )
 ,则C的实轴长为( )
,则C的实轴长为( )
A .  B .
B .  C . 4
D . 8
C . 4
D . 8
 B .
B .  C . 4
D . 8
C . 4
D . 8
一机构随机调查了某小区100人的月收入情况,将所得数据按  ,
,  ,
,  ,
,  ,
,  ,
,  (单位:元)分成六组,并且作出如图所示的频率分布直方图.
(单位:元)分成六组,并且作出如图所示的频率分布直方图.
 ,
,  ,
,  ,
,  ,
,  ,
,  (单位:元)分成六组,并且作出如图所示的频率分布直方图.
(单位:元)分成六组,并且作出如图所示的频率分布直方图. 
-
(1) 根据频率分布直方图估计样本数据的中位数;
-
(2) 根据题目分组情况,按分层抽样的方法在
 ,
,  ,
,  三组中抽取6人,再从这6人中抽取2人,求至少有一人收入在
三组中抽取6人,再从这6人中抽取2人,求至少有一人收入在  的概率.
的概率.
已知数列  是首项为1的等差数列,且公差不为零.而等比数列
是首项为1的等差数列,且公差不为零.而等比数列  的前三项分别是
的前三项分别是  ,
,  ,
,  .
.
 是首项为1的等差数列,且公差不为零.而等比数列
是首项为1的等差数列,且公差不为零.而等比数列  的前三项分别是
的前三项分别是  ,
,  ,
,  .
.
-
(1) 求数列
 的通项公式
的通项公式  ;
;
-
(2) 若b1+b2+……+bk=85,求正整数k的值.
已知函数![]() ,且
,且![]() .
.
(1)判断函数![]() 的单调性;
的单调性;
(2)若方程![]() 有两个根为
有两个根为![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.

已![]() 知函数
知函数![]() 在R上单调递减,且
在R上单调递减,且![]() ,则
,则![]() 的取值范围为
的取值范围为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() ( )
( )
定义运算![]() 为执行如图所示的程序框图输出的s值,则
为执行如图所示的程序框图输出的s值,则![]() 的值为( )
的值为( )
A.4 B.3 C.2 D.—1

最近更新
- 噬菌体侵染大肠杆菌实验不能说明的是 A.DNA是主要的遗传物质 B.DNA能自我复制 C.DNA是遗传物
- 如图6甲所示为杂技表演的安全网示意图,网绳的结构为正方格形,O、a、b、c、d…等为网绳的结点.安全网水平张紧后,若质量
- (本小题满分14分)若点,在中按均匀分布出现.(1)点横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则
- I don’t likemath. It’s _________. A. funny
- 当前源于美国的金融危机是1929至1933年“大萧条”以来华尔街遭遇的最严 危机,百年一遇,蔓延迅速。阅读下列材料回答问
- (08年惠州一中四模理) 如图,将圆分成个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种
- 的值为______.
- 下列不属于新事物的是( ) ①苏联解体,东欧演变 ②我国社会主义现代化建设与改革开放 ③比较完备的、成熟的资本
- 2012年1月10日,聊城电视台天气预报:“聊城明天天气多云转晴,北风转南风3—4级,湖面4—5级。最低气温:-6℃左右
- He sat _______ to her______ the stairs. A. to listen; to c
- 观察H2燃烧产生火焰的颜色时,燃气导管口的材料最好用( ) A.钠玻璃 B.钾玻璃
- Secret codes (密码)keep messages private. Banks, companies, an
- 我国于2010年11月1日正式启动的第六次全国人口普查已经完成。通过普查能掌握准确的人口数量、人口素质、人口结构和人口分
- 部分十一届全国人大代表到某市进行实地视察,听取了该市政府的工作汇报,并就百姓关心的突出问题提出了合理化建议。这说明 A.
- 材料一:2008年我国企业景气和企业家信心指数 注:受国际金融危机的影响,2008年我国GDP增长9%,同比回落2个多百
- “五十六个民族,五十六枝花,五十六个兄弟姐妹是一家……”这首歌唱出了各族人民的心声。请你判断,我国人口最多的少数民族主
- 指出下列句中成语的错误 1 对于房价在全国略胜一筹的北京来说,经济适用房的低价位无疑对工薪阶层具有巨大的吸引力。 2
- 由函数确定数列,,若函数的反函数能确定数列,,则称数列是数列的“反数列”. (1)若函数确定数列的反数列为,求的通项公式
- 将栽有刚发芽的玉米幼苗的小盆固定于如图所示的以一定速度匀速旋转的转盘上(小盆不透光),并给予左侧光照。一段时间后,玉米的
- 写作 阅读下列文字,按要求作文。 电脑键盘上有许多功能键:CTRL+C复制,CTRL+X剪切,CTRL+V粘贴,CTRL



