高中 数学
从2名教师和5名学生中,选出3人参加“我爱我的祖国”主题活动.要求入选的3人中至少有一名教师,则不同的选取方案的种数是( )
A . 20
B . 55
C . 30
D . 25
已知 , 则tan2α=( )
, 则tan2α=( )
 , 则tan2α=( )
, 则tan2α=( )
A .  B .
B .  C . -
C . - D . -
D . -
 B .
B .  C . -
C . - D . -
D . -
设函数f(x)定义在R上,它的图像关于直线x=1对称,且当x≥1时,f(x)=3x﹣1,则有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知 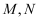 是互不重合的直线,
是互不重合的直线,  是互不重合的平面,下列四个命题中正确的是( )
是互不重合的平面,下列四个命题中正确的是( )
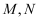 是互不重合的直线,
是互不重合的直线,  是互不重合的平面,下列四个命题中正确的是( )
是互不重合的平面,下列四个命题中正确的是( )
A . 若  ,则
,则  B . 若
B . 若  ,则
,则  C . 若
C . 若  ,则
,则  D . 若
D . 若  ,则
,则 
 ,则
,则  B . 若
B . 若  ,则
,则  C . 若
C . 若  ,则
,则  D . 若
D . 若  ,则
,则 
若函数 恰有四个单调区间,则实数m的取值范围( )
恰有四个单调区间,则实数m的取值范围( )
 恰有四个单调区间,则实数m的取值范围( )
恰有四个单调区间,则实数m的取值范围( )
A .  B .
B .  且
且 C .
C .  D .
D . 
 B .
B .  且
且 C .
C .  D .
D . 
有如图所示的程序框图,则该程序框图表示的算法的功能是( )
A . 输出使 成立的最小整数n.
B . 输出使
成立的最小整数n.
B . 输出使 成立的最大整数n.
C . 输出使
成立的最大整数n.
C . 输出使 成立的最大整数n+2.
D . 输出使
成立的最大整数n+2.
D . 输出使 成立的最小整数n+2.
成立的最小整数n+2.
 成立的最小整数n.
B . 输出使
成立的最小整数n.
B . 输出使 成立的最大整数n.
C . 输出使
成立的最大整数n.
C . 输出使 成立的最大整数n+2.
D . 输出使
成立的最大整数n+2.
D . 输出使 成立的最小整数n+2.
成立的最小整数n+2.
各项均为正数的数列 的前n项和为
的前n项和为 ,
,  , 数列
, 数列 为等比数列,且
为等比数列,且 .
.
 的前n项和为
的前n项和为 ,
,  , 数列
, 数列 为等比数列,且
为等比数列,且 .
.
-
(1) 求数列
 、
、 的通项公式;
的通项公式;
-
(2) 记
 ,
,  为数列
为数列 的前n项和,对任意的
的前n项和,对任意的 .
. 恒成立,求
恒成立,求 及实数的
及实数的 取值范围.
取值范围.
已知函数 若
若 , 则
, 则 ( )
( )
 若
若 , 则
, 则 ( )
( )
A . 7
B . -2
C . 2
D . 7或-2
已知向量  ,
,  满足
满足  ,
,  ,
,  ,则
,则  与
与  的夹角为( )
的夹角为( )
 ,
,  满足
满足  ,
,  ,
,  ,则
,则  与
与  的夹角为( )
的夹角为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知公差小于零的等差数列{an}的前n项和为Sn , 且满足a3a4=117,a2+a5=22.
-
(1) 求数列{an}的通项公式;
-
(2) 求Sn的最大值.
下列对条件语句的描述正确的是( )
A . ELSE后面的语句不可以是条件语句
B . 两个条件语句可以共用一个END IF语句
C . 条件语句可以没有ELSE后的语句
D . 条件语句中IF—THEN和ELSE后的语句必须都有
已知函数  ,(
,(  )是偶函数.
)是偶函数.
 ,(
,(  )是偶函数.
)是偶函数.
-
(1) 求
 的值;
的值;
-
(2) 设函数
 ,其中
,其中  .若函数
.若函数  与
与  的图象有且只有一个交点,求
的图象有且只有一个交点,求  的取值范围.
的取值范围.
已知函数f(x)=  ﹣
﹣  +x+d在R上单调,则b的取值范围为.(用区间表示)
+x+d在R上单调,则b的取值范围为.(用区间表示)
 ﹣
﹣  +x+d在R上单调,则b的取值范围为.(用区间表示)
+x+d在R上单调,则b的取值范围为.(用区间表示)
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(Ⅰ)求该几何体的体积V;
(Ⅱ)求该几何体的面积S.

与圆(x﹣3)2+(y﹣3)2=8相切,且在x、y轴上截距相等的直线有( )
A . 4条
B . 3条
C . 2条
D . 1条
如图,在![]() △
△![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() .
.
(Ⅰ)求证:![]() 是△
是△![]() 的外接圆的切线;
的外接圆的切线;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.

 如图, 直线y=
如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点.
(1) 求点Q的坐标;
(2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.
从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为
A.2097 B.2264 C.2111 D.2012
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
… | |||||||
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ![]() )的周期为π,且图象上的一个最低点为M(
)的周期为π,且图象上的一个最低点为M(![]() ).
).
(1)求f(x)的解析式及单调递增区间;
(2)当x∈[0,![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )
A . ![]() a2 B.
a2 B. ![]() a2 C.
a2 C. ![]() a2 D.
a2 D. ![]() a2
a2
最近更新
- 利用反应6NO2+8NH3===7N2+12H2O构成电池的方法,既能实现有效消除氮氧化物的排放,减轻环境污染,又能充分
- 以下措施都能使海洋钢质钻台增强抗腐蚀能力,其中属于“牺牲阳极的阴极保护法”的是() A.对钢材“发蓝”(钝化) B
- —_________ —Yes,D-E-S-K. A. Can you spell i
- 设全集U={x},集合A={x},B={x2+px+12=0},且(CUA)B={1,4,3,5},求实数P、q的值。
- “世上疮痍,诗中圣哲;民间疾苦,笔底波澜。”郭沫若这副对联是称赞下列哪位诗人的( ) A 杜甫 B李白
- 阅读下面材料,根据自己的感悟和联想,写一篇不少于800字的文章。 章太炎读了许多中医著作,自认为医术高明,喜好替人医病,
- 《〈论语〉十则》中最早由儒家提倡的待人接物的处世之道的句子是: 。
- 读图为“城市人口比重变化折线图”,回答1-2题1.下列叙述正确的是 ( ) A.图中甲曲线表示发展中国家,乙曲
- 如图所示,物体A、B的质量分别是、,用轻弹簧相连接放在光滑的水平面上,物体B左侧与竖直墙相接触.另有一个物体C以速度向左
- 2005年2月16日,旨在要求相关签约成员减少温室气体排放的国际性条约《京都议定书》正式生效。《京都议定书》是1997年
- 现有一量程为3V的电压表,内阻约为5kΩ~6kΩ。为了较准确地测量其内电阻,在没有电流表的情况下,某同学设计了如图甲所示
- 以下关于菌种保藏的叙述,错误的是( )。 A.菌种保藏的目的是保持菌种的纯净 B.固体斜面培养基可用于菌种的临时保藏
- 材料一:我国宪法规定:“中华人民共和国的一切权力属于人民。人民行使国家权力 的机关是全国人民代表大会和地方各级人民代表大
- 如图5,在四棱柱ABCDA1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,
- 3月27日,2011年女子冰壶世锦赛上中国队险胜丹麦队夺得铜牌.如图9所示,比赛中两名队员在冰壶前方“刷冰”,这是通过
- (本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分 . 设函数的最大值为,最小值为, 其中. (1)
- On April 9,2010,a solar-powered plane successfully made its
- 2013年暑假期间,某学校课题研究小组为了撰写关于未知材料电阻率的实践报告,设计了一个测量电阻率(被测电阻丝的阻值约为2
- 联合国卫生组织经过严密的科学分析,认为我国的铁锅是最理想的炊具,并向全世界大力推广,其主要原因是A.价格便宜
- 地球上陆地面积约占( ) A.29% B.48% C.71%




