高中 数学
一物体在力F(x)=3x2﹣2x+3的作用下沿与力F(x)相同的方向由x=1m运动到x=5m时F(x)做的功为.
若复数z满足  ,其中
,其中 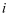 为虚数单位,则
为虚数单位,则  ( )
( )
 ,其中
,其中 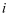 为虚数单位,则
为虚数单位,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知非零向量 满足
满足 ,
,  , 则
, 则 .
.
 满足
满足 ,
,  , 则
, 则 .
.
第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,为了保护各国元首的安全,将5个安保小组全部安排到指定三个区域内工作,且这三个区域每个区域至少有一个安保小组,则这样的安排的方法共有( )
A . 96种
B . 100种
C . 124种
D . 150种
能得出 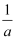 <
< 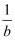 成立的是( )
成立的是( )
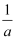 <
< 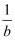 成立的是( )
成立的是( )
A .  B .
B .  C .
C .  D .
D . 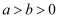
 B .
B .  C .
C .  D .
D . 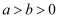
在同一坐标系中,函数y=2x与y=  的图象之间的关系是( )
的图象之间的关系是( )
 的图象之间的关系是( )
的图象之间的关系是( )
A . 关于y轴对称
B . 关于x轴对称
C . 关于原点对称
D . 关于直线y=x对称
将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,若函数
的图象,若函数 在区间
在区间 上单调递增,则
上单调递增,则 的值可能为( )
的值可能为( )
 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,若函数
的图象,若函数 在区间
在区间 上单调递增,则
上单调递增,则 的值可能为( )
的值可能为( )
A .  B .
B .  C . 3
D . 4
C . 3
D . 4
 B .
B .  C . 3
D . 4
C . 3
D . 4
函数y=2x﹣x2的大致图象应是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某车间20名工人年龄数据如表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(Ⅰ) 求这20名工人年龄的众数与平均数;
(Ⅱ) 以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(Ⅲ) 从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
已知直线  与圆
与圆  交于
交于  ,
,  两点,则
两点,则  的最小值为.
的最小值为.
 与圆
与圆  交于
交于  ,
,  两点,则
两点,则  的最小值为.
的最小值为.
在我国南北朝时期,数学家祖暅在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.其意思是,用一组平行平面截两个几何体,若在任意等高处的截面面积都对应相等,则两个几何体的体积必然相等.根据祖暅原理,“两几何体A、B的体积不相等”是“A、B在等高处的截面面积不恒相等”的( )条件
A . 充分不必要
B . 必要不充分
C . 充要
D . 既不充分也不必要
在 中,若
中,若 , 则
, 则 是 ( )
是 ( )
 中,若
中,若 , 则
, 则 是 ( )
是 ( )
A . 等腰或直角三角形
B . 等腰三角形
C . 直角三角形
D . 钝角三角
函数  的单调递增区间是( )
的单调递增区间是( )
 的单调递增区间是( )
的单调递增区间是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知角  的终边经过点
的终边经过点  ,则( )
,则( )
 的终边经过点
的终边经过点  ,则( )
,则( )
A .  B .
B .  C .
C .  D . 若
D . 若  为钝角,则
为钝角,则 
 B .
B .  C .
C .  D . 若
D . 若  为钝角,则
为钝角,则 
点M(x,y)是不等式组  表示的平面区域Ω内的一动点,且不等式2x﹣y+m≥0恒成立,则的取m值范围是( )
表示的平面区域Ω内的一动点,且不等式2x﹣y+m≥0恒成立,则的取m值范围是( )
 表示的平面区域Ω内的一动点,且不等式2x﹣y+m≥0恒成立,则的取m值范围是( )
表示的平面区域Ω内的一动点,且不等式2x﹣y+m≥0恒成立,则的取m值范围是( )
A . m≥3﹣2  B . m≥3
C . m≥0
D . m≥1﹣2
B . m≥3
C . m≥0
D . m≥1﹣2 
 B . m≥3
C . m≥0
D . m≥1﹣2
B . m≥3
C . m≥0
D . m≥1﹣2 
设![]() 为等差数列
为等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
某个实心零部件的形状是如图所示的几何体,其下部是底面均是正
方形,侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD,上部是
一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
ABCD-A2B2C2D2.
(1)证明:直线B1D1⊥平面ACC2A2;
(2)现需要对该零部件表面进行防腐处理,已知AB=10![]() ,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?
,A1B1=20,AA2=30,AA1=13(单位:厘米),每平方厘米的加工处理费为0.20元,需加工处理费多少元?

.sin 1,sin 2,sin3的大小关系为… …( )
A.sin 1<sin 2< sin3 B.sin 2<sin3 <sin 1
C.sin 3<sin 2< sin1 D.sin3<sin 1< sin2
若幂函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]() 的值为__________.
的值为__________.
若![]() 、
、![]() ,则“
,则“![]() ”是“
”是“![]() ”成立的
”成立的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
最近更新
- 读图,完成下面试题。图中Q地的年降雪日数可能是 A.8天 B.12天 C.9天 D.4天 造成P地一月等温线向北弯
- 下列物质的性质,不是由于氢键引起的是 A.沸点:H2O>H2S B.溶解性:NH3(易溶
- (2012·河南省中考试题) 下列词语中加点的字,每对读音都不相同的一项是( ) A扭转/纽带 粗犷/旷日持久 哽
- 2008年5月16日人民币对美元汇率中间价报6.9895,较前一交易日走高105个基点。这意味着 ①美元兑换人民币的汇率
- 用某人的胰岛素基因制成的DNA探针,检测下列物质,能形成杂交分子的是 ( ) ①该人胰
- 下列消毒产品,消毒效果最好的可能是( ) A.84消毒液
- 某混合气体可能含CO、CO2、NH3、HCl、H2和H2O(g)中的一种或几种,当依次通过澄清石灰水(无浑浊现象)、氢氧
- Y元素最高正价与负价的绝对值之差是4;Y元素与M 元素形成化合物,并在水中电离出电子层结构相同的离子,该化合物是(
- 与黄土高原处在同一个地势阶梯的地形区是 A.山东丘陵
- 在撇开其他因素影响的前提下,下列图示能体现价格对商品需求量影响情况的是(y轴为需求量,x轴为价格)
- ,然后天梯石栈相钩连。上有六龙回日之高标, 。
- 用惰性电极电解下列溶液一段时间后,再加入一定量的某种物质(括号内物质),能够使溶液恢复到原来的成分和浓度的是( ) A
- 下列属于伯里克利时代的雅典民主政治主要表现包括:①对某些别有企图的野心家制定了“陶片放逐法”②除十将军以外,各级官职向公
- 下列各组中的两种物质作用时,反应条件或反应物用量改变时,对生成物没有影响的是 A.Na2O2与CO2 B.Na与O2
- 读图回答下列问题。 湄公河是一条国际河流。2008年3月3日,围绕加强资源、能源合理利用,扩大贸易市场等问题,湄公河流域
- 下列话语不应该出自孔子的是:() A.“性本善” B.“为政以德”
- 设函数,曲线在点处的切线方程为. (1)求的解析式; (2)证明:曲线上任一点处的切线与直线和直线所围成的三角形面积
- —What could I get my father for Father's Day?—___________get
- If you travel or go abroad, it’s necessary tomix with the lo
- I canthink of many cases ______ students obviously know a l



