高中 数学
 或
或  ,
,  .
.
-
(1) 当
 时,求
时,求  ;
;
-
(2) 若
 ,求实数
,求实数  的取值范围.
的取值范围.
 的总体抽取容量为
的总体抽取容量为  的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率依次为
的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率依次为  ,
,  ,
,  ,则( ).
,则( ).
 B .
B .  C .
C .  D .
D . 
 ,其中
,其中  .
.-
(1) 当
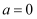 时,求
时,求  的最小值;
的最小值;
-
(2) 若
 有三个不同的单调区间,求实数
有三个不同的单调区间,求实数  的取值范围.
的取值范围.
 的双曲线
的双曲线 ﹣
﹣ =1(a>0,b>0)称为黄金双曲线.给出以下几个说法:
=1(a>0,b>0)称为黄金双曲线.给出以下几个说法:(1)双曲线x2﹣ =1是黄金双曲线;
=1是黄金双曲线;
(2)若b2=ac,则该双曲线是黄金双曲线;
(3)若MN经过右焦点F2且MN⊥F1F2 , ∠MON=90°,则该双曲线是黄金双曲线;
(4)若F1 , F2为左右焦点,A1 , A2为左右顶点,B1(0,b),B2(0,﹣b)且∠F1B1A2=90°,则该双曲线是黄金双曲线. 其中正确命题的序号为
 、
、  、
、  和实数λ,下列正确的是( )
和实数λ,下列正确的是( )
 •
•  =0,则
=0,则  =0或
=0或  =0
B . 若λ
=0
B . 若λ  =0,则λ=0或
=0,则λ=0或  =
=  C . 若
C . 若  2=
2=  2 , 则
2 , 则  =
=  或
或  =﹣
=﹣  D . 若
D . 若  •
•  =
=  •
•  ,则
,则  =
= 
 =a+bx,则最小二乘法的思想是( )
=a+bx,则最小二乘法的思想是( )
 [yi﹣(ai+bxi)]最小
B . 使得
[yi﹣(ai+bxi)]最小
B . 使得  |yi﹣(ai+bxi)|最小
C . 使得
|yi﹣(ai+bxi)|最小
C . 使得  [yi2﹣(ai+bxi)2]最小
D . 使得
[yi2﹣(ai+bxi)2]最小
D . 使得  [yi﹣(ai+bxi)]2最小
[yi﹣(ai+bxi)]2最小
 相切的半径最小的圆方程是( )
相切的半径最小的圆方程是( )
 B .
B .  C .
C .  D .
D . 
 是方程
是方程  的两根,角
的两根,角  满足:
满足:  ,求角
,求角  的度数,边
的度数,边  的长度及
的长度及  的面积.
的面积. 是等差数列
是等差数列  的前
的前  项和,若
项和,若  ,则
,则  .
.
 中,四边形
中,四边形 为菱形,
为菱形, , 则
, 则 .
.
 中,
中,  是棱
是棱  的中点,已知
的中点,已知  底面
底面  ,
,  ,
, 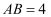 ,
,  ,则异面直线
,则异面直线  ,
,  所成角的正弦值为( )
所成角的正弦值为( ) 
 B .
B .  C .
C .  D .
D . 
 ,
,  满足
满足  •(
•(  +
+  )=5,且|
)=5,且|  |=2,|
|=2,|  |=1,则
|=1,则  与
与  夹角的大小为.
夹角的大小为.在(1-x)5+(1-x)6+(1-x)7+(1-x)8的展开式中,含x3的项的系数是________.
-121 [展开式中含x3的项的系数为
设![]() ,
,![]() 分别是椭圆E:
分别是椭圆E:![]() +
+![]() =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过![]() 的直线与E相交于A、B两点,且
的直线与E相交于A、B两点,且![]() ,
,![]() ,
,![]() 成等差数列。
成等差数列。
(1)求![]() 的周长
的周长
(2)求![]() 的长
的长
(3)若直线的斜率为1,求b的值。
在平面直角坐标系xOy中,以原点为极点,以x轴正半轴为极轴建立极坐标系,已知曲线C1的参数方程为![]()
![]() (α为参数),曲线C2的方程为x2+(y﹣4)2=16.
(α为参数),曲线C2的方程为x2+(y﹣4)2=16.
(Ⅰ)求曲线C1的极坐标方程;
(Ⅱ)若曲线θ=![]()
![]() (ρ>0)与曲线C1.C2交于A,B两点,求|AB|.
(ρ>0)与曲线C1.C2交于A,B两点,求|AB|.
某电脑公司有5名产品推销员,其工作年限与年推销金额的数据如表:
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限 | 3 | 5 | 6 | 7 | 9 |
| 推销金额 | 2 | 3 | 3 | 4 | 5 |

![]() 求年推销金额y关于工作年限x的线性回归方程;
求年推销金额y关于工作年限x的线性回归方程;
![]() 判断变量x与y之间是正相关还是负相关;
判断变量x与y之间是正相关还是负相关;
![]() 若第6名推销员的工作年限是11年,试估计他的年推销金额.
若第6名推销员的工作年限是11年,试估计他的年推销金额.
(参考数据 ,
, ,
,
参考公式:线性回归方程![]() 中,
中,![]() ,其中
,其中![]() 为样本平均数)
为样本平均数)
已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=![]() ,A+C=2B,求:角A的大小.
,A+C=2B,求:角A的大小.
在![]() ABC中,
ABC中,![]() ,
,![]() ,A=30°,则B解的个数是( ).
,A=30°,则B解的个数是( ).
A.0个 B.1个 C.2个 D.不确定的
设a=log2![]() ,b=(
,b=(![]() )3,c=3
)3,c=3![]() ,则( )
,则( )
A.c<b<a B.a<b<c C.c<a<b D.b<a<c
已知集合![]() ,集合
,集合![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
- 在“测定小灯泡的额定功率”的实验中,小灯泡的额定电压为2.5V,小灯泡的电阻大约为10Ω。(1)实验电路图如图8所示,请
- 武侠电影里经常描写一大侠双目失明,还能判断出攻击者的方位,这是因为:A.他的眼睛根本就没有失明;B.他的耳朵有特异功能;
- When I was nineyears old, I loved to go fishing with my
- 如图1,抛物线y=ax2+bx -1经过A(-1,0)、B(2,0)两点,交y轴于点C.点P为抛物线上的一个动点,过点P
- 25. ______, a small advertisement held my attention, which r
- 在化学反应6CO2+6H2OC6H12O6+6O2中没有涉及到的物质类别是() A.单质 B.氧化物 C.盐 D
- 材料一 质询权是目前人大监督工作中的一个热点。所谓质询,是指各级人大代表或人大常委会组成人员,按照法律规定的程序,对本级
- 进行化学实验时,下列应急措施正确的是 ( )
- 18.根据下面的材料,根据要求写一篇不少于800字的文章。 与其他手机公司相比,化为公司28年坚持只做一件事,就是对准通
- 围绕新文化运动提出“打倒孔家店”的口号,某班学生展开评论。你认为哪一评论是不妥当的 A、这一口号体现了对东西方文化的
- 用NA表示阿伏加德罗常数的值。下列叙述中正确的是() A.标准状况下,0.1 mol Cl2溶于水,转移的电子数目为0.
- “PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,它造成的雾霾天气对人体健康的危害甚至要比沙尘暴更大.环境检
- 阅读下面的《论语》选段,回答问题。 孔子于乡党,恂恂①如也,似不能言者。其在宗庙、朝廷,便便②言,唯谨尔。 [注] ①恂
- 人民网正式推出“直通中南海——中央领导人和中央机构留言板”。该留言板突出互动性,旨在让广大网友对中央领导人倾诉心声,给中
- 汽车尾气排放的CO、NOx等气体是大气污染的主要来源,NOx也是雾霾天气的主要成因之一。 i.在汽车排气管加装催化转化器
- 在十二届全国人大的2987名代表中,工人、农民、知识分子、解放军、民主党派、港澳及归国华侨等各占一定比例。这充分说明我国
- 中国特色社会主义理论体系就是包括 等重大战略思想在内的科学理论体系,是马克思主义中国化的最新理论成果。 ①生态文
- 同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为.但n为100时,应如何计算正方形的具体个数
- 下列食品添加剂中,其使用目的与反应速率有关的是 A.抗氧化剂 B.调味剂 C.着色剂
- 在距地面高为h的光滑水平桌面上,一个轻弹簧左端固定,右端紧挨一质量为m的小球。用小球压缩弹簧后放手,小球沿水平桌面滑动后



