高中 数学
设函数  ,点
,点  (
(  ),
),  为坐标原点,设向量
为坐标原点,设向量  ,若向量
,若向量  ,且
,且  是
是  与
与  的夹角,记
的夹角,记  为数列
为数列  的前n项和,则
的前n项和,则  ,
,  .
.
 ,点
,点  (
(  ),
),  为坐标原点,设向量
为坐标原点,设向量  ,若向量
,若向量  ,且
,且  是
是  与
与  的夹角,记
的夹角,记  为数列
为数列  的前n项和,则
的前n项和,则  ,
,  .
.
抛物线 上与焦点的距离等于6的点横坐标是( )
上与焦点的距离等于6的点横坐标是( )
 上与焦点的距离等于6的点横坐标是( )
上与焦点的距离等于6的点横坐标是( )
A . 1
B . 2
C . 3
D . 4
设  为非零向量,则“
为非零向量,则“  ”是“
”是“  与
与  共线”的( )
共线”的( )
 为非零向量,则“
为非零向量,则“  ”是“
”是“  与
与  共线”的( )
共线”的( )
A . 充分而不必要条件
B . 必要而不充分条件
C . 充要条件
D . 既不充分也不必要条件
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.

(Ⅰ)求直方图中x的值;
(Ⅱ)试估计所抽取的数学成绩的平均数;
(Ⅲ)试根据样本估计“该校高一学生期末数学考试成绩≥70”的概率.
已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:
x | 1 | 2 | 3 |
f(x) | 2 | 3 | 1 |
g(x) | 3 | 2 | 1 |
则关于x的方程g(f(x))=x的解是x=.
如图,  的二面角的棱上有
的二面角的棱上有  两点,直线
两点,直线  分别在这个二面角的两个半平面内,且都垂直于
分别在这个二面角的两个半平面内,且都垂直于  .已知
.已知  ,则
,则  的长为
的长为
 的二面角的棱上有
的二面角的棱上有  两点,直线
两点,直线  分别在这个二面角的两个半平面内,且都垂直于
分别在这个二面角的两个半平面内,且都垂直于  .已知
.已知  ,则
,则  的长为
的长为 
A .  B . 7
C .
B . 7
C .  D . 9
D . 9
 B . 7
C .
B . 7
C .  D . 9
D . 9
已知函数 则( )
则( )
 则( )
则( )
A .  的单调递减区间为
的单调递减区间为 B .
B .  的解集为
的解集为 C . 若
C . 若 有三个不同的根,则实数
有三个不同的根,则实数 D .
D .  存在最大值3和最小值2
存在最大值3和最小值2
 的单调递减区间为
的单调递减区间为 B .
B .  的解集为
的解集为 C . 若
C . 若 有三个不同的根,则实数
有三个不同的根,则实数 D .
D .  存在最大值3和最小值2
存在最大值3和最小值2
对任意函数  ,
,  ,可按如图所示的程序框图构造一个数列发生器,记由数列发生器产生数列
,可按如图所示的程序框图构造一个数列发生器,记由数列发生器产生数列  ,
,  .
.
 ,
,  ,可按如图所示的程序框图构造一个数列发生器,记由数列发生器产生数列
,可按如图所示的程序框图构造一个数列发生器,记由数列发生器产生数列  ,
,  .
.
(Ⅰ)若定义函数  ,且输入
,且输入  ,请写出数列
,请写出数列  的所有项;
的所有项;
(Ⅱ)若定义函数  ,且输入
,且输入  ,求数列
,求数列  的通项公式
的通项公式  .
.
在四面体  中,
中,  ,二面角
,二面角  的大小为
的大小为 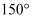 ,则四面体
,则四面体  外接球的半径为.
外接球的半径为.
 中,
中,  ,二面角
,二面角  的大小为
的大小为 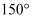 ,则四面体
,则四面体  外接球的半径为.
外接球的半径为.
已知复数z满足  ,则
,则  的最大值是.
的最大值是.
 ,则
,则  的最大值是.
的最大值是.
设函数 , 若对任意的实数a,b,总存在
, 若对任意的实数a,b,总存在 使得
使得 成立,则实数
成立,则实数 的最大值为( )
的最大值为( )
 , 若对任意的实数a,b,总存在
, 若对任意的实数a,b,总存在 使得
使得 成立,则实数
成立,则实数 的最大值为( )
的最大值为( )
A . -1
B . 0
C .  D . 1
D . 1
 D . 1
D . 1
设  ,且
,且  ,则下列各不等式中恒成立的是( )
,则下列各不等式中恒成立的是( )
 ,且
,且  ,则下列各不等式中恒成立的是( )
,则下列各不等式中恒成立的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知实数x,y满足条件  ,则z=y﹣2x的最小值为.
,则z=y﹣2x的最小值为.
 ,则z=y﹣2x的最小值为.
,则z=y﹣2x的最小值为.
求圆心在y轴上,且与直线l1:4x-3y+12=0, 直线l2:3x-4y-12=0都相切的圆的方程.
已知函数f(x)=lnx+![]()
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m![]() R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n>![]() ∈N*).
∈N*).
设α为第四象限的角,若![]() ,则tan2α=_______________。
,则tan2α=_______________。
已知向量![]() ,
,![]() ,函数
,函数![]() ,(x∈R)。
,(x∈R)。
(1)求函数![]() 的最大值及其相对应的x值;
的最大值及其相对应的x值;
(2)求函数![]() 的单调增区间.
的单调增区间.
用辗转相除法求840与1764的最大公约数.
已知函数![]() (常数
(常数![]() 且
且![]() ).
).
(1)证明:当![]() 时,函数
时,函数![]() 有且只有一个极值点;
有且只有一个极值点;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,证明:
,证明:![]() 且
且![]() .
.
![]() 的值为
的值为
最近更新
- 肼(N2H4)是一种无色油状液体,完全燃烧的反应方程式如下:N2H4+O2=X+2H2O,放出大量的热.下列有关说法不正
- 下列说法不正确的是A.氢氟酸能和玻璃的成分SiO2发生化学反应 B.根据SiO2+Na2CO3Na2SiO3+CO2↑的
- “忠孝”是儒家传统的核心要义之一,在专制等级社会,“忠孝”往往意味着臣子无条件效忠皇帝和儿女无条件服从父母。但在今天,“
- 在顶端优势现象中,侧芽生长素浓度总是高于顶芽,但是顶芽产生的生长素仍大量积存于侧芽部位,这种生长素极性运输的特性是因为生
- 请在下面横线上填写相应的句子(15分) (1) ,
- 物体在同一位置做平抛运动,下列说法正确的是( ) A.落地前物体每秒的速度增量总是大小相等,方向相同 B.物体落地
- 下列关于生命活动调节的叙述正确的是:() A.血浆渗透压下降时引起口渴 B.在冬季时健康人机体产热多于散热
- 综合性学习(共3分) 10.在北京市第29个义务植树日到来之际,某校开展了关于义务植树的调查活动,下面是活动小组搜集到的
- Some people think clowns are only funny for children. ______
- 下列有关肽键写法中,不正确的是() A. B.﹣CO﹣NH﹣ C. D.
- 18.下列对散文《我与地坛》选段的理解与分析,不恰当的一项是 我常觉得这中间有着宿命的味道:仿佛这古园就是为了等我,而历
- HEMA是制备软质隐形眼镜的材料,其名称是聚甲基丙烯酸羟乙酯,则合成它的单体应为( ) D.CH3—CH=CH—C
- 实验室制取气体选择收集方法时,对气体的下列性质不必考虑的是A.颜色B.密度C.溶解性D.是否与水反应
- 下列关于中和热的说法中正确的是() A.10 L 0.05mol·L-1Ba(OH)2溶液与20 L 0.05mol·L
- 0<a<1,不等式>1的解是 () A.x>a B.a<x<1
- Eat less food _______ you want to put on weight . A. if
- 计算:852﹣152=()A. 70 B. 700 C. 4900 D. 7000
- 根据下面例句的句式和含义,仿写两个句子。 例句: 脆弱的时候,就看山,因为大山有一种硬度;得意的时候,就眺海,因为大海有
- (2009年海淀模拟)环境因素对生物生长、发育、生殖、行为和分布等有直接或间接的影响。下列关于环境因素对生物影响的叙述,
- ____ since the night before, I felt very hungry. A. Having e



