高中 数学
已知函数  .
.
 .
.
-
(1) 若
 在
在  单调递增,求
单调递增,求  的取值范围:
的取值范围:
-
(2) 若
 ,证明:当
,证明:当  时,
时,  .
.
已知函数  ,
,  .
.
 ,
,  .
.
-
(1) 若
 ,求曲线
,求曲线  在点
在点  处的切线方程;
处的切线方程;
-
(2) 若函数
 在
在  上是减函数,求实数
上是减函数,求实数  的取值范围.
的取值范围.
如图2﹣①,一个圆锥形容器的高为a,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为  (如图2﹣②),则图2﹣①中的水面高度为.
(如图2﹣②),则图2﹣①中的水面高度为.
 (如图2﹣②),则图2﹣①中的水面高度为.
(如图2﹣②),则图2﹣①中的水面高度为. 
已知  ,
,  是两个平面,
是两个平面,  ,
,  是两个条件,则下列结论正确的是( )
是两个条件,则下列结论正确的是( )
 ,
,  是两个平面,
是两个平面,  ,
,  是两个条件,则下列结论正确的是( )
是两个条件,则下列结论正确的是( )
A . 如果  ,
,  ,那么
,那么  B . 如果
B . 如果  ,
,  ,
,  ,那么
,那么  C . 如果
C . 如果  ,
,  ,那么
,那么  D . 如果
D . 如果  ,
,  且
且  ,那么
,那么 
 ,
,  ,那么
,那么  B . 如果
B . 如果  ,
,  ,
,  ,那么
,那么  C . 如果
C . 如果  ,
,  ,那么
,那么  D . 如果
D . 如果  ,
,  且
且  ,那么
,那么 
已知数1、a、b成等差数列,而1、b、a成等比数列,若a≠b,则a的值为( )
A . - B .
B .  C .
C .  D . -
D . -
 B .
B .  C .
C .  D . -
D . -
已知函数f(x)=|x﹣a|.
(1)若f(x)≤m的解集为{x|﹣1≤x≤5},求实数a,m的值.
(2)当a=2且0≤t<2时,解关于x的不等式f(x)+t≥f(x+2).
下列函数中是奇函数,又在定义域内为减函数的是( )
A . 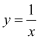 B .
B .  C .
C . 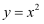 D .
D . 
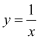 B .
B .  C .
C . 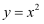 D .
D . 
已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,1].
(Ⅰ)求m的值;
(Ⅱ)若a,b,c∈R,且  =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.
已知函数f(x)=alnx+b(a,b∈R),曲线f(x)在x=1处的切线方程为x﹣y﹣1=0.
-
(1) 求a,b的值;
-
(2) 证明:f(x)+
 ≥1;
≥1;
-
(3) 已知满足xlnx=1的常数为k.令函数g(x)=mex+f(x)(其中e是自然对数的底数,e=2.71828…),若x=x0是g(x)的极值点,且g(x)≤0恒成立,求实数m的取值范围.
把﹣ 化成角度是( )
化成角度是( )
 化成角度是( )
化成角度是( )
A . ﹣960°
B . ﹣480°
C . ﹣120°
D . ﹣60°
设集合S={ },在S上定义运算为:
},在S上定义运算为: 其中k为i+j被4除的余数,i、j=0,1,2,3.满足关系式
其中k为i+j被4除的余数,i、j=0,1,2,3.满足关系式 的x(x∈S)的个数为( )
的x(x∈S)的个数为( )
 },在S上定义运算为:
},在S上定义运算为: 其中k为i+j被4除的余数,i、j=0,1,2,3.满足关系式
其中k为i+j被4除的余数,i、j=0,1,2,3.满足关系式 的x(x∈S)的个数为( )
的x(x∈S)的个数为( )
A . 4
B . 3
C . 2
D . 1
抛物线  的准线方程为( )
的准线方程为( )
 的准线方程为( )
的准线方程为( )
A . 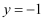 B .
B . 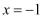 C .
C .  D .
D . 
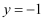 B .
B . 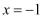 C .
C .  D .
D . 
已知:函数  对一切实数x , y都有
对一切实数x , y都有  成立,且
成立,且  .
.
 对一切实数x , y都有
对一切实数x , y都有  成立,且
成立,且  .
.
-
(1) 求
 的值.
的值.
-
(2) 求
 的解析式.
的解析式.
-
(3) 已知
 ,设P:当
,设P:当  时,不等式
时,不等式  恒成立;Q:当
恒成立;Q:当  时,
时,  是单调函数.如果满足P成立的a的集合记为A , 满足Q成立的a的集合记为B , 求
是单调函数.如果满足P成立的a的集合记为A , 满足Q成立的a的集合记为B , 求  (
(  为全集).
为全集).
已知角  的终边经过点
的终边经过点  .
.
 的终边经过点
的终边经过点  .
.
-
(1) 求
 ,
,  ;
;
-
(2) 求
 的值.
的值.
已知奇函数f(x)=  的定义域为R,其中g(x)为指数函数且过点(2,9).
的定义域为R,其中g(x)为指数函数且过点(2,9).
 的定义域为R,其中g(x)为指数函数且过点(2,9).
的定义域为R,其中g(x)为指数函数且过点(2,9). (Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)判断函数f(x)的单调性,并用函数单调性定义证明.
已知函数  ,则
,则  的值等于( )
的值等于( )
 ,则
,则  的值等于( )
的值等于( )
A . 2
B . 7
C . -4
D . -7
一条线段的长是5,它的一个端点A(2,1),另一端点B的横坐标是-1,则B的纵坐标是( )
A.-3 B.5
C.-3或5 D.-5或3
函数![]() 的定义域为 ( )
的定义域为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
设O为坐标原点,直线![]() 与抛物线
与抛物线![]() 交于D,E两点,若
交于D,E两点,若![]() ,则C的焦点坐标为
,则C的焦点坐标为
A. (![]() ,0)
,0)
B. (![]() ,0)
,0)
C. (1,0)
D. (2,0)
在![]() 中,角
中,角![]() 对边分别为
对边分别为![]() ,角
,角![]() ,且
,且![]() .
.
(1)证明:![]() ;
;
(2)若![]() 面积为1,求边
面积为1,求边![]() 的长.
的长.
最近更新
- 将3.42 g蔗糖和3.24 g淀粉的混合物完全水解后共生成a g葡萄糖和b g果糖,则a与b的比值为( ) A.
- 在⊙O中,弦AB=2cm,圆心角=60°,则⊙O的直径为___________cm。
- A new bridge ____ across the river and is expected to open n
- 某离子晶体的晶胞结构如图3-25所示。试求: 图3-25(1)晶体中每个Y同时吸引着__________个X,每个X同
- 亚非大陆是人类文明的摇篮,尼罗河流域的古埃及文明的标志是A.金字塔 B.长城 C.种姓制
- 阅读下面的文字,完成下面试题。 李白的诗歌固然有高超的艺术技巧,但若论章法的严密、用典的巧妙、对偶的工整,未必就比其他诗
- 分子式为C5H10O3的有机物,在一定条件下能发生如下反应:①在浓硫酸存在下,能分别与CH3CH2OH或CH3COOH反
- 20世纪以来,国际关系格局经历了凡尔赛---华盛顿体系、两极格局到多极化趋势的演进。前两次格局与多极化趋势相比,不同点是
- (15分)为了实验“神舟六号”飞船安全着陆,在飞船距离地面约1m时(即将着陆前的瞬间),安装在返回舱底部的四台发动机同时
- 填入下文方框内最恰当的一句是: ( ) 她已年过半百,对于演员,年龄是大了些。可是, . A只要听她唱,就会觉得她
- 两极格局结束的根源在于( )A.苏联解体,东欧剧变 B.第三世界的崛起C.美国咄咄逼人
- 图3-6-12所示的电路原来是接通的,在时刻突然打开开关S,则通过电阻的电流随时间的变化图象应是图3-6-13中的()
- 中俄天然气管道东线开工仪式于2014年9月1日举行。根据双方商定,从2018年起,俄罗斯开始通过中俄天然气管道东线
- 陈独秀在《前锋》杂志上撰文认为:“殖民地半殖民地的社会阶级固然一体幼稚,然而资产阶级的力量究竟比农民集中,比工人雄厚”。
- 在酸性溶液中,能大量共存的离子组是 A.K+、NH4+、NO3-、SO42- B.K+、Na
- 下边是某同学在历史课堂笔记上记下的关键词。该同学学习的应是() A.新中国成立 B.社会主义制度确立 C.“” D.改革
- 云冈石窟位于下列哪一省区 A.陕西 B.山西
- 下列各组词语中,有错别字的一组是 A.委曲 委屈求全
- 2009年国庆节期间,《建国大业》、《天安门》等影片给观众带来了新的感受,取得了票房和口碑的“双赢”。这些影片之所以能征
- 由欧姆定律公式可知() A.同一导体两端的电压跟通过导体的电流成反比 B.导体两端的电压为零时,因为没有电流通过,所以导



