高中 数学
直线  被圆
被圆  截得的弦长为( )
截得的弦长为( )
 被圆
被圆  截得的弦长为( )
截得的弦长为( )
A . 4
B .  C .
C . 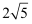 D .
D . 
 C .
C . 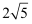 D .
D . 
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=  ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为  ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )
 ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为  ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( ) 
A . “弦”  米,“矢”
米,“矢”  米
B . 按照经验公式计算所得弧田面积(
米
B . 按照经验公式计算所得弧田面积(  )平方米
C . 按照弓形的面积计算实际面积为(
)平方米
C . 按照弓形的面积计算实际面积为(  )平方米
D . 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据
)平方米
D . 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据 
 )
)
已知a,b∈R* , 且ab2=4,则a+b的最小值为.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼 的时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外课外体育运动时间在[40,60)上的学生评价为“课外体育达标”.
-
(1) 请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标
课外体育达标
合计
男
女
20
110
合计
参考公式:
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.参考数据:
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
-
(2) 将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为X,若每次抽取的结果是相互独立的,求X的数学期望和方差.
已知  ,其中
,其中  为常数,若
为常数,若  ,则
,则  =.
=.
 ,其中
,其中  为常数,若
为常数,若  ,则
,则  =.
=.
已知函数  (
(  ,
,  )恒过定点
)恒过定点  ,则函数
,则函数  的图像不经过( )
的图像不经过( )
 (
(  ,
,  )恒过定点
)恒过定点  ,则函数
,则函数  的图像不经过( )
的图像不经过( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
若向量  与
与  的夹角为锐角,则m的取值范围是.
的夹角为锐角,则m的取值范围是.
 与
与  的夹角为锐角,则m的取值范围是.
的夹角为锐角,则m的取值范围是.
已知函数f(x)=﹣x2+2bx+c,设函数g(x)=|f(x)|在区间[﹣1,1]上的最大值为M.
-
(1) 若b=2,试求出M;
-
(2) 若M≥k对任意的b、c恒成立,试求k的最大值.
椭圆  的长轴长、短轴长、离心率依次是( )
的长轴长、短轴长、离心率依次是( )
 的长轴长、短轴长、离心率依次是( )
的长轴长、短轴长、离心率依次是( )
A . 7,2,  B . 14,4,
B . 14,4,  C . 7,2,
C . 7,2,  D . 14,4,
D . 14,4, 
 B . 14,4,
B . 14,4,  C . 7,2,
C . 7,2,  D . 14,4,
D . 14,4, 
已知集合  ,若集合
,若集合  恰有8个子集,则
恰有8个子集,则  的取值范围是( )
的取值范围是( )
 ,若集合
,若集合  恰有8个子集,则
恰有8个子集,则  的取值范围是( )
的取值范围是( )
A . (-2,-1]
B . [-2,-1)
C . [-1,0)
D . (-1,0]
设F1 , F2是椭圆 的两个焦点,点P在椭圆上,且F1P⊥PF2 , 则△F1PF2的面积为
的两个焦点,点P在椭圆上,且F1P⊥PF2 , 则△F1PF2的面积为
 的两个焦点,点P在椭圆上,且F1P⊥PF2 , 则△F1PF2的面积为
的两个焦点,点P在椭圆上,且F1P⊥PF2 , 则△F1PF2的面积为
已知数列{an}是各项正数首项1等差数列,Sn为其前n项和,若数列{  }也为等差数列,则
}也为等差数列,则  的最小值是.
的最小值是.
 }也为等差数列,则
}也为等差数列,则  的最小值是.
的最小值是.
已知(2﹣  x)50=a0+a1x+a2x2+…+a50x50 , 其中a0 , a1 , …a50是常数,计算:
x)50=a0+a1x+a2x2+…+a50x50 , 其中a0 , a1 , …a50是常数,计算:
 x)50=a0+a1x+a2x2+…+a50x50 , 其中a0 , a1 , …a50是常数,计算:
x)50=a0+a1x+a2x2+…+a50x50 , 其中a0 , a1 , …a50是常数,计算:
-
(1) a0+a1+a2+…+a50;
-
(2) a0+a2+…+a50;
-
(3) a10;
-
(4) (a0+a2+a4+…+a50)2﹣(a1+a3+…+a49)2 .
已知平面  的法向量为
的法向量为  ,点
,点  在平面
在平面  内,若点
内,若点  到平面
到平面  的距离
的距离  为
为 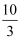 ,则
,则 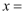 .
.
 的法向量为
的法向量为  ,点
,点  在平面
在平面  内,若点
内,若点  到平面
到平面  的距离
的距离  为
为 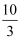 ,则
,则 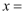 .
.
已知![]() ,
,![]() ,若向量
,若向量![]() 与
与![]() 共线,则
共线,则![]() 和
和![]() 方向上的投影为 .
方向上的投影为 .
已知正三棱锥SABC的底面边长为4,高为3,在正三棱锥内任取一点P,使得VPABC<![]() VSABC的概率是________.
VSABC的概率是________.
设函数![]() .
.
(1)若![]() ,求
,求![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 时,
时, ![]() 的值域为
的值域为![]() ,求
,求![]() 的值.
的值.
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第![]() 个图形包含
个图形包含![]() 个小正方形.则
个小正方形.则![]() 的表达式为_________.
的表达式为_________.

函数 的值域是_____________.
的值域是_____________.
最近更新
- 为解决“相权”对“皇权”的威胁,中国历代统治者采取了许多措施。下面有一组关于汉代以后,历朝限制丞相权力的说法。根据你的理
- However, happened later proved me wrong. A.what B.that C.whi
- 用呼吸抑制剂处理红细胞,其对下列物质吸收量显著减少的是() A.乙醇和苯 B. O2和H2
- 阅读下面的文字,完成后面各题。 快手刘 冯骥才 ①人人在童年,都是时间的富翁。有时呆在家里闷得慌,或者父亲嫌我太闹,打发
- 下列四幅图片中,能够反映热带草原景观的是( )
- 下列各组词语中有错别字的一组是( ) A. 重叠 迭挫强敌 文彩 神采奕奕 B. 泄露
- After months of voyage, Columbusarrived in ______ later pro
- 无论是什么性质的国家,通常都设有国家元首。下列对于国家元首的正确认识有 A. 国家元首是一个国家的最高领导人 B. 国家
- 日光灯电路主要由镇流器、启运器和灯管组成,下列说法正确的是A.灯管正常发光后,启动器两个触片是连接的B.灯管正常发光后,
- 虾青素(C40H52O4)是一种具有极强的抗肿瘤、抗氧化性能的物质,可增强动物免疫能力。下列有关它的说法正确的是
- 诗言志。从李白“长风破浪会有时,”的诗句中,我们能感受到诗人乘长风破万里浪,挂上云帆,横渡沧海,到达理想彼岸的豪情;从杜
- 林则徐在给道光皇帝的奏稿中提出:“迨(等到)流毒于天下……数十年后,中原几无可以御敌之兵,且无可以充饷之银……(白银)果
- New York, London, Paris and other big cities are exciting pl
- 下列山脉中,属东西走向最北的一列是:( ) A.大兴安岭-太行山 B.昆仑山-秦岭 C.南岭
- 右图是某品牌服装标签。下列有关错误的是( ) A.羊毛属于合成纤维 B.该服装面料不耐高温 C.羊毛和涤纶可用燃烧
- ---Which is ______, the sun, the moon or the earth? ---Of
- 如图2-4-7所示,电压U保持不变,当滑片由a端移到b端的过程中,R1两端电压变化的范围从U到5U/6,则滑动变阻器总阻
- 20世纪以来,苏俄、美国、中国在现代化道路的探索中进行了各自的实践,开创了不同杜会制度下社会改革经济发展的模式。阅读以下
- .1967年马丁•路德荣登《时代周刊》封面,目的是褒扬马丁•路德对人类进步所作的贡献。马丁•路德的宗教改革在促进思想解放
- 右图为等高线地形图,其代表某种文化景观,读图回答8-9题。8.该种文化景观是: A.小溪 B.梯田 C.平原




