高中 数学
方程  的实数根所在的区间为( )
的实数根所在的区间为( )
 的实数根所在的区间为( )
的实数根所在的区间为( )
A .  B .
B . 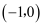 C .
C .  D .
D . 
 B .
B . 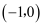 C .
C .  D .
D . 
已知  对任意的
对任意的  恒成立,若
恒成立,若  ,则
,则 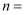 .
.
 对任意的
对任意的  恒成立,若
恒成立,若  ,则
,则 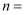 .
.
如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若  四点均位于图中的“晶格点”处,且
四点均位于图中的“晶格点”处,且  的位置所图所示,则
的位置所图所示,则  的最大值为.
的最大值为.
 四点均位于图中的“晶格点”处,且
四点均位于图中的“晶格点”处,且  的位置所图所示,则
的位置所图所示,则  的最大值为.
的最大值为.
下列说法正确的是( )
A . 坐标平面内的任何一条直线均有倾斜角
B . 不经过原点的直线都可以用方程
 表示
C . 直线
表示
C . 直线
 ,
,
 , 则与直线
, 则与直线
 与
与
 距离相等的直线方程为
距离相等的直线方程为
 D . 已知圆
D . 已知圆
 , 圆心为
, 圆心为
 ,
,
 为直线
为直线
 上一动点,过点
上一动点,过点
 向圆
向圆
 引两条切线
引两条切线
 和
和
 ,
,
 、
、
 为切点,则四边形
为切点,则四边形
 的面积的最小值为
的面积的最小值为

 表示
C . 直线
表示
C . 直线
 ,
,
 , 则与直线
, 则与直线
 与
与
 距离相等的直线方程为
距离相等的直线方程为
 D . 已知圆
D . 已知圆
 , 圆心为
, 圆心为
 ,
,
 为直线
为直线
 上一动点,过点
上一动点,过点
 向圆
向圆
 引两条切线
引两条切线
 和
和
 ,
,
 、
、
 为切点,则四边形
为切点,则四边形
 的面积的最小值为
的面积的最小值为

已知函数f(x)=x2﹣4|x|+3.
-
(1) 试证明函数f(x)是偶函数;
-
(2) 画出f(x)的图象;(要求先用铅笔画出草图,再用中性笔描摹)
-
(3) 请根据图象指出函数f(x)的单调递增区间与单调递减区间;(不必证明)
-
(4) 当实数k取不同的值时,讨论关于x的方程x2﹣4|x|+3=k的实根的个数.
若方程  有实数根
有实数根  ,则称
,则称  为函数
为函数  的一个不动点,已知函数
的一个不动点,已知函数  .
.
 有实数根
有实数根  ,则称
,则称  为函数
为函数  的一个不动点,已知函数
的一个不动点,已知函数  .
.
-
(1) 若
 ,求证:
,求证:  有唯一不动点;
有唯一不动点;
-
(2) 若
 有两个不动点,求实数a的取值范围.
有两个不动点,求实数a的取值范围.
 的大小关系为( )
的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知灯塔 在海洋观察站
在海洋观察站 的北偏东50°的方向上,灯塔
的北偏东50°的方向上,灯塔 在海洋观察站
在海洋观察站 的南偏东70°的方向上,
的南偏东70°的方向上, ,
,  两点间的距离为5海里,
两点间的距离为5海里, ,
,  两点间的距离为7海里,则
两点间的距离为7海里,则 ,
,  两点间的距离为( )海里.
两点间的距离为( )海里.
 在海洋观察站
在海洋观察站 的北偏东50°的方向上,灯塔
的北偏东50°的方向上,灯塔 在海洋观察站
在海洋观察站 的南偏东70°的方向上,
的南偏东70°的方向上, ,
,  两点间的距离为5海里,
两点间的距离为5海里, ,
,  两点间的距离为7海里,则
两点间的距离为7海里,则 ,
,  两点间的距离为( )海里.
两点间的距离为( )海里.
A . 3
B . 4
C . 6
D . 8
某城市随机抽取一年(365天)内100天的空气质量指数  (Air Pollution Index)的监测数据,结果统计如下:
(Air Pollution Index)的监测数据,结果统计如下:
 (Air Pollution Index)的监测数据,结果统计如下:
(Air Pollution Index)的监测数据,结果统计如下:
|
|
|
|
|
|
| 大于300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重 污染 | 重度污染 |
天数 | 10 | 15 | 20 | 30 | 7 | 6 | 12 |
(Ⅰ)若本次抽取的样本数据有30天是在供暖季,其中有7天为重度污染,完成下面  列联表,并判断能否有
列联表,并判断能否有  的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: 
(Ⅱ)政府要治理污染,决定对某些企业生产进行管控,当  在区间
在区间  时企业正常生产;当
时企业正常生产;当  在区间
在区间  时对企业限产
时对企业限产  (即关闭
(即关闭  的产能),当
的产能),当  在区间
在区间  时对企业限产
时对企业限产 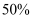 ,当
,当  在300以上时对企业限产
在300以上时对企业限产  ,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
,企业甲是被管控的企业之一,若企业甲正常生产一天可得利润2万元,若以频率当概率,不考虑其他因素:
①在这一年中随意抽取5天,求5天中企业被限产达到或超过 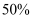 的恰为2天的概率;
的恰为2天的概率;
②求企业甲这一年因限产减少的利润的期望值.
过点  作直线
作直线  ,与抛物线
,与抛物线  只有一个公共点,满足条件的直线有( )
只有一个公共点,满足条件的直线有( )
A . 0条
B . 3条
C . 2条
D . 1条
下列命题中,正确的命题是 



A . 任意三点确定一个平面
B . 三条平行直线最多确定一个平面
C . 不同的两条直线均垂直于同一个平面,则这两条直线平行
D . 一个平面中的两条直线与另一个平面都平行,则这两个平面平行
已知向量  与
与  的夹角为
的夹角为  ,
,  ,
,  ,则
,则  .
.
 与
与  的夹角为
的夹角为  ,
,  ,
,  ,则
,则  .
.
已知全集  ,集合
,集合  ,则
,则  =.
=.
 ,集合
,集合  ,则
,则  =.
=.
若过点  可作圆
可作圆  的两条切线,则实数
的两条切线,则实数  的取值范围为.
的取值范围为.
 可作圆
可作圆  的两条切线,则实数
的两条切线,则实数  的取值范围为.
的取值范围为.
已知函数 .
.
 .
.
-
(1) 判定函数
 的单调性;
的单调性;
-
(2) 若
 时,
时, , 求实数a的取值范围.
, 求实数a的取值范围.
在①  ;②
;②  这两个条件中任选一个作为已知条件,补充到下面的横线上并作答.
这两个条件中任选一个作为已知条件,补充到下面的横线上并作答.
 ;②
;②  这两个条件中任选一个作为已知条件,补充到下面的横线上并作答.
这两个条件中任选一个作为已知条件,补充到下面的横线上并作答. 问题:在  中,角A,B,C的对边分别为a,b,c,已知___________.
中,角A,B,C的对边分别为a,b,c,已知___________.
-
(1) 求角A;
-
(2) 若
 ,求
,求  的周长.
的周长. 注:如果选择多个条件分别解答,按第一个解答计分.
已知圆C1的方程为(x-2)2+(y-1)2=![]() ,椭圆C2的方程为
,椭圆C2的方程为![]() =1(a>b>
=1(a>b>
0),C2的离心率为![]() ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程
已知曲线![]() .
.
(1)求曲线![]() 在(1,1)点处的切线的方程;
在(1,1)点处的切线的方程;
(2)求由曲线![]() 、直线
、直线![]() 和直线所围成图形的面积.
和直线所围成图形的面积.
已知函数:![]() ,其中:
,其中:![]() ,记函数
,记函数![]() 满足条件:
满足条件:![]() 为事件为A,则事件A发生的概率为( )
为事件为A,则事件A发生的概率为( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则截去的几何体
是( )

A. 三棱锥 B. 三棱柱 C. 四棱锥 D. 四棱柱
是( )

A. 三棱锥 B. 三棱柱 C. 四棱锥 D. 四棱柱
最近更新
- 16.卢作孚于1926年创办的民生实业股份有限公司,其章程曰:以个人影响社会,以事业影响环境,以社会影响国家,个人为事业
- 古希腊哲学家泰勒斯有句名言:“水是万物之源”;我国古代也有“五行说”,认为世界是由金、木、水、火、土演化而来。这两种哲学
- 下列鉴别物质的方法能达到实验目的的是 ( ) A.用澄清石
- . 明清时期,阻碍近代科学在中国产生的最主要原因是() A.闭关锁国的实行 B.八股取士
- 阅读下列材料: 材料一:北京大学发行杂志多种,转以提倡过激派伪说。平时教授学生也本此旨。此次罢学风潮,近因虽由政治问题以
- 水是生命之源,也是人类宝贵的资源.请用化学知识回答下列问题: (1)自来水厂在净水时,加入明矾的目的是. (2)生活中将
- 用一个平面去截一个圆柱体,不可能的截面是( ). A. B. C.D.
- 下列几种物质的用途说法正确的是A.氨气可以用来保存粮食、水果B.福尔马林稀溶液可用于各种水产品保鲜C.二氧化硫可以使酸性
- 材料:海尔停产非节水型洗衣机,只生产达到国家A级标准的洗衣机,这将推动中国的洗衣机产品向着节水环保方向发展。由于我国众多
- 函数与的图象在同一平面直角坐标系内的交点的个数是( ) A、1个 B、2个
- 1978年以来,国有企业改革不断深化。在改革中,党中央做出了关于国有企业改革和发展若干重大问题的决定,颁布了国有企业党员
- 沙特阿拉伯的贝都因人的住房通常是:A.高脚屋 B.帐篷 C.木屋D.冰屋
- 铝能制成铝箔是因为铝具有A.延展性B.导电性C.导热性D.抗腐蚀性
- 如图所示,光滑水平桌面上,有物体A、B用轻弹簧相连,两物块质量相等,即mA=mB,在水平拉力FA和FB的作用下一起运动,
- 在pH=1的溶液中能大量共存的一组离子或分子是 ( )A. Na+、Mg2+、ClO-、NO3-
- 下列关于实验现象的描述,正确的是A.蜡烛在氧气中燃烧产生大量的白烟B.木炭在空气中燃烧呈红热状态C.铜片在空气中加热表面
- 直线l的极坐标方程为,圆C的极坐标方程为.则直线l和圆C的位置关系为
- (3分)氢气是一种清洁能源,它燃烧后只生成水对环境无污染。若使40g的氢气完全燃烧,消耗氧气的质量是多少克?
- 下列关于误差的说法中正确的是: A.认真细致的测量可以避免误差 B.测量时未遵守操作规则会引起误差 C.测量时的错误就是
- 阅读下面的文字,完成1-4题。 地效飞行器——“鹈鹕” 几十年来,美国军队的机动性一直是最让五角大楼关注的问题。建立一支











