高中 数学
如图,在四面体ABCD中,若截面PQMN是正方形,则在下列命题中,不一定正确的是( )

A . AC⊥BD
B . AC∥截面PQMN
C . AC = BD
D . 异面直线PM与BD所成的角为 
已知数列  满足:
满足:  .
.
 满足:
满足:  .
. (Ⅰ)若  ,且
,且  ,
,  ,
,  成等比数列,求
成等比数列,求  ;
;
(Ⅱ)若  ,且
,且  ,
,  ,
,  ,
,  成等差数列,求
成等差数列,求  .
.
已知数列  中,
中,  ,且
,且  ,
,  ,则数列
,则数列  的前20项和为.
的前20项和为.
 中,
中,  ,且
,且  ,
,  ,则数列
,则数列  的前20项和为.
的前20项和为.
函数f(x)=sinωx(ω>0),对任意实数x有  ,且
,且  ,那么
,那么  =( )
=( )
 ,且
,且  ,那么
,那么  =( )
=( )
A . a
B .  C .
C .  D . ﹣a
D . ﹣a
 C .
C .  D . ﹣a
D . ﹣a
某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球占用时间的情况,采用分层抽样的方法,收集300位业务足球运动员每周平均踢足球占用时间的样本数据(单位:小时)
得到业余足球运动员每周平均踢足球所占用时间的频率分布直方图(如图所示),其中样本数据分组区间为:(0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
将“业务运动员的每周平均踢足球时间所占用时间超过4小时”
定义为“热爱足球”.
附:K2= 
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |

-
(1) 应收集多少位女运动员样本数据?
-
(2) 估计该地区每周平均踢足球所占用时间超过4个小时的概率.
-
(3) 在样本数据中,有80位女运动员“热爱足球”.请画出“热爱足球与性别”列联表,并判断是否有99%的把握认为“热爱足球与性别有关”.
设  为
为  所在平面内一点,
所在平面内一点,  ,
,  ,
,  ,则
,则  ( )
( )
 为
为  所在平面内一点,
所在平面内一点,  ,
,  ,
,  ,则
,则  ( )
( )
A . 20
B . -20
C . 12
D . -12
在  中,角A,B,C所对的边分别为a,b,c,满足
中,角A,B,C所对的边分别为a,b,c,满足  ,点D,E满足
,点D,E满足  ,
,  .
.
 中,角A,B,C所对的边分别为a,b,c,满足
中,角A,B,C所对的边分别为a,b,c,满足  ,点D,E满足
,点D,E满足  ,
,  .
.
-
(1) 求
 的大小;
的大小;
-
(2) 若
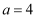 ,
,  ,求b,c.
,求b,c.
将函数  的图象上各点的横坐标缩小为原来的
的图象上各点的横坐标缩小为原来的  ,再向右平移
,再向右平移  个单位后得到的图象关于直线
个单位后得到的图象关于直线  对称,则
对称,则  的最小值是( )
的最小值是( )
 的图象上各点的横坐标缩小为原来的
的图象上各点的横坐标缩小为原来的  ,再向右平移
,再向右平移  个单位后得到的图象关于直线
个单位后得到的图象关于直线  对称,则
对称,则  的最小值是( )
的最小值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知偶函数  满足:
满足:  ,并且当
,并且当  时,
时,  ,函数
,函数  与函数
与函数  的交点个数是.
的交点个数是.
 满足:
满足:  ,并且当
,并且当  时,
时,  ,函数
,函数  与函数
与函数  的交点个数是.
的交点个数是.
设a、b为实数,函数f(x)=ax+b满足:对任意x∈[0,1],有1≥|f(x)|,则ab的最大值为.
设抛物线C:y2=3px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为
cos  的值为( )
的值为( )
 的值为( )
的值为( )
A .  B . ﹣
B . ﹣  C . ﹣
C . ﹣  D .
D . 
 B . ﹣
B . ﹣  C . ﹣
C . ﹣  D .
D . 
已知1>a>b>c>0,且a,b,c依次成等比数列,设m=logab,n=logbc,p=logca,则m、n、p的大小关系为( )
A . p>n>m
B . m>p>n
C . p>m>n
D . m>n>p
数列  中,
中,  ,
,  ,且
,且  .
.
 中,
中,  ,
,  ,且
,且  .
.
-
(1) 令
 ,将
,将  用
用  表示,并求
表示,并求  通项公式;
通项公式;
-
(2) 令
 ,求证:
,求证:  .
.
已知数列{an}中,  ,(n∈N+),则在数列{an}的前50项中最小项和最大项分别是( )
,(n∈N+),则在数列{an}的前50项中最小项和最大项分别是( )
 ,(n∈N+),则在数列{an}的前50项中最小项和最大项分别是( )
,(n∈N+),则在数列{an}的前50项中最小项和最大项分别是( )
A . a1 , a50
B . a1 , a8
C . a8 , a9
D . a9 , a50
化简计算:
-
(1) 计算:
 ;
;
-
(2) 化简:
 .
.
设命题![]() :实数
:实数![]() 满足
满足![]() ;命题
;命题![]() :实数
:实数![]() 满足
满足![]() ;命题
;命题![]() :实数
:实数![]() 满足
满足![]() 的集合为
的集合为![]() .
.
(1) 若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
(2) 若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
已知在函数![]() (
(![]() )的所有切线中,有且仅有一条切线与直线
)的所有切线中,有且仅有一条切线与直线![]() 垂直.
垂直.
(1)求的值和切线的方程;
(2)设曲线![]() 在任一点处的切线倾斜角为
在任一点处的切线倾斜角为![]() ,求
,求![]() 的取值范围.
的取值范围.
已知![]() ,且
,且![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
函数![]() 的最小正周期T为_______.
的最小正周期T为_______.
最近更新
- 为了得到函数的图象,只需把函数的图象上所有的点的 ( )
- 第二节:书面表达(满分25分) 下图是你校2009年在水电、学生用纸、学生伙食人均费用与2008年比较的增长情况。从图表
- NaHSO4在水溶液中能够电离出H+、Na+、和SO42-。下列对于NaHSO4的分类中不正确的是( ) A.NaH
- 在中,分别为角的对边,且,则( ) A.成等比数列 B.成等差数列 C.成等比数列
- 某地区一些玉米植株比一般玉米植株早熟,生长整齐而健壮,且果穗大,籽粒多.这些植株可能是 (
- He started to explain, but she cut him short,_____ she had t
- 动物细胞工程技术的基础是 A 动物细胞融合 B 胚胎移植 C 动物细胞培养
- O2F2可以发生反应:H2S+4O2F2=SF6+2HF+4O2,下列说法正确的是( ) A.氧气是氧化产物 B.O
- 阅读《与女儿沟通音乐》回答问题。 像大多数女孩一样,我女儿喜欢听流行音乐,对走红的港台歌星如数家珍,书桌周围的墙
- 阅读下列材料,结合所学知识回答问题。 材料一 口述史是记录历史的古老形式,唐德刚给口述史注入了新的因素,树立了活的范例
- “上得山丘好,欢乐含苦辛。请勿歌仰止,雄峰正相迎”这首诗启示我们实现人生价值 ①需要社会提供一定的客观条件 ②要有顽强拼
- 已知函数(,),. (Ⅰ)证明:当时,对于任意不相等两个正实数、,均有 ; (Ⅱ)记, (ⅰ)若在上单调递增,求实数的取
- 下列变化中,属于化学变化的是() A.酒精挥发B.矿石粉碎C.木材燃烧D.干冰升华
- “铁、铜、铝、锌”是生活中常见的金属 (1)人体缺 元素会引起食欲不振,生长迟缓,发育不良; (2)铜丝常用来作电
- 下面对有关名著名篇的说明,不正确的两项是(5分) 附加题A.《雷雨》的作者曹禺把三十多年间发生过的事情,集中地放在周公
- 阅读下面的文字,完成19―22题,(共19分)看花的姿态 迟子健我是白先勇先生的读者。他的《永远的尹雪艳》和《金大班的
- 下面各组词语中有错别字的一项是 ( )3分 A、崎岖 麻木不仁 粗制滥造
- 原子是构成物质的基本粒子。下列有关原子的叙述错误的是( ) A原子在化学变化中能够再分 B.原子质量很小 C.原子
- 读图,回答14﹣16题.14.图中,学校在农业实验区的方向.( ) A.西南 B.东北
- (7分)下图是某草原生态系统中部分生物之间关系的示意图,请据图回答:(1)生态系统中的生物成分包括生产者、消费者、 _



