高中 数学
函数f(x)=  的定义域为
的定义域为
 的定义域为
的定义域为
设集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C . 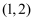 D .
D . 
 B .
B .  C .
C . 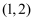 D .
D . 
在正方体ABCD﹣A1B1C1D1中,M,N是棱A1B1 , B1B的中点,求异面直线AM和CN所成角的余弦值.

{an} 是首项为1,公差为2的等差数列,令bn=a3n , 则数列 {bn} 的一个通项公式是( )
A . bn=3n+2
B . bn=4n+1
C . bn=6n﹣1
D . bn=8n﹣3
若直线y=﹣x+1的倾斜角为  ,则
,则 
 ,则
,则 
A .  B . 1
C .
B . 1
C .  D .
D . 
 B . 1
C .
B . 1
C .  D .
D . 
 的值为.
的值为.
已知f(x)=| ﹣
﹣ x|﹣|
x|﹣|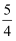 +
+ x|
x|
 ﹣
﹣ x|﹣|
x|﹣|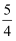 +
+ x|
x|(Ⅰ)关于x的不等式f(x)≥a2﹣3a恒成立,求实数a的取值范围;
(Ⅱ)若f(m)+f(n)=4,且m<n,求m+n的取值范围.
某高中数学社团招募成员,依次进行笔试,面试两轮选拔,每轮结果都分“合格”和“不合格”.当参选同学在第一轮笔试中获得“合格”时,才能进入下一轮面试选拔,两轮选拔都合格的同学入选到数学社团.现有甲同学参加数学社团选拔,已知甲同学在笔试,面试选拔中获得“合格”和“不合格”的概率分别为 ,
,  , 且在笔试,面试两轮选拔中取得的成绩均相互独立,互不影响且概率相同,则甲同学能进入到数学社团的概率是,设甲同学在本次数学社团选拔中恰好通过X轮选拔,则数学期望
, 且在笔试,面试两轮选拔中取得的成绩均相互独立,互不影响且概率相同,则甲同学能进入到数学社团的概率是,设甲同学在本次数学社团选拔中恰好通过X轮选拔,则数学期望 .
.
 ,
,  , 且在笔试,面试两轮选拔中取得的成绩均相互独立,互不影响且概率相同,则甲同学能进入到数学社团的概率是,设甲同学在本次数学社团选拔中恰好通过X轮选拔,则数学期望
, 且在笔试,面试两轮选拔中取得的成绩均相互独立,互不影响且概率相同,则甲同学能进入到数学社团的概率是,设甲同学在本次数学社团选拔中恰好通过X轮选拔,则数学期望 .
.
已知数列 是等比数列,且
是等比数列,且 , 公比
, 公比
 是等比数列,且
是等比数列,且 , 公比
, 公比
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 数列
 满足
满足 ,
,  , 求数列
, 求数列 的前
的前 项和
项和 的最小值
的最小值
若当  时,不等式
时,不等式  恒成立﹐则实数
恒成立﹐则实数  的取值范围是.
的取值范围是.
 时,不等式
时,不等式  恒成立﹐则实数
恒成立﹐则实数  的取值范围是.
的取值范围是.
如图是指数函数①  、②
、②  、③
、③  、④
、④  的图像,则a,b,c,d与1的大小关系是( )
的图像,则a,b,c,d与1的大小关系是( )
 、②
、②  、③
、③  、④
、④  的图像,则a,b,c,d与1的大小关系是( )
的图像,则a,b,c,d与1的大小关系是( ) 
A . c<d<1<a<b
B . d<c<1<b<a
C . c<d<1<b<a
D . 1<c<d<a<b
“10既是自然数又是偶数”为形式.(填“p∧q”或“p∨q”)
设全集 ,
,  ,
,  , 则图中阴影部分表示的集合为( )
, 则图中阴影部分表示的集合为( )
A .  B .
B .  C . [-1,0)
D .
C . [-1,0)
D . 
 B .
B .  C . [-1,0)
D .
C . [-1,0)
D . 
已知全集为  ,集合
,集合  ,
,  ,则
,则  .
.
 ,集合
,集合  ,
,  ,则
,则  .
.
在△ABC中,内角A,B,C所对边分别为a,b,c,且a=3b,sinB=  ,则sinA等于( )
,则sinA等于( )
 ,则sinA等于( )
,则sinA等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,
,  ,则
,则  .
.
 ,
,  ,则
,则  .
.
若  ,且
,且  .
.
 ,且
,且  .
.
-
(1) 求
 ,
,  ,
,  ,
,  ,
,
-
(2) 归纳猜想通项公式
 ,用数学归纳法证明.
,用数学归纳法证明.
选修4—1:几何证明选讲
如图,AB是⊙O的直径,C,F是⊙O上的点,OC垂直于直径AB,过F点作⊙O的切线交AB的延长线于D.连结CF交AB于E点.
(1)求证:DE2=DB·DA;
(2)若⊙O的半径为![]() ,OB=
,OB=![]() OE,求EF的长.
OE,求EF的长.

集合![]() ,
,![]() ,则A∩B=( )
,则A∩B=( )
A.{x|2<x≤3} B.{x|2≤x≤3} C.{x|1≤x<4} D.{x|1<x<4}
若![]() 且
且![]() ,则
,则![]() 在( )
在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
最近更新
- 第三部分:阅读理解(共20小题,每题2分,满分40分) 阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳
- 如果从政府角度,给下面漫画拟写一个标题,最佳的是( )A.公共权力 切莫乱用 B.加强管理 依法执政 C.接
- 木炭在空气燃烧的现象是木炭红热,在氧气中燃烧发出白光放出大量的热,硫在空气中燃烧产生淡蓝火焰放出热,在氧气中产生蓝紫火焰
- 图中的A、B、C三图表示基因、DNA、染色体的关系,D图表示李冰同学的体细胞内一对染色体上的一对基因D、d,请回答下列问
- 书面表达 根据汉语提示,写出意思连贯、符合逻辑、不少于80词的短文。 假设你叫陈泉,昨天收到了笔友David的e-mai
- 在构建社会主义和谐社会过程中,建立适合社会主义市场经济要求的社会保障制度必须坚持的原则有 ( ) ①
- “吃一碗方便面需要32天解毒”,“wifi辐射会严重损害身体健康”,类似的“科学流言”在微信朋友圈中时常可见。传播的流言
- 在二项式的展开式中,的系数是,则实数的值为_________.
- 19.补写出下列句子中的空缺部分。(1)苏轼在《赤壁赋》中慨叹“人生短促,人很渺小”的句子是:“ ,
- 已知NaHSO3溶液显酸性,溶液中存在以下平衡: HSO3-+H2OH2SO3+OH- ① HSO3-H++SO
- 我国的植物资源十分丰富,其中居世界首位的是( ) A.藻类植
- 根据金属活动顺序表的有关知识,回答下列问题: (1)用Mg、Zn、Cu三种金属分别与稀盐酸反应,根据金属与稀盐酸反应的
- 2.下列各句中,没有语病的一项是( ) A.劳动者的时间都去哪儿了?据调查结果显示,中国九成行业周工时超过40小时,
- 已知:如图,正方形ABCD的边长为a,BM,DN分别平分正方形的两个外角,且满足,连结MC,NC,MN.【小题1】(1)
- 某几何体的三视图如图所示,则此几何体是()A.圆锥 B.圆柱 C.长方体 D.四棱柱
- 向体积为2 L的固定密闭容器中通入3molX气体,在一定温度下发生如下反应: 2X(g) Y(g)+3Z(g) (1)
- I don't ________ ghosts but I do ________ my eyes -- I saw i
- 据图的演讲内容,该演讲者的主题是( ) 在佛山某中学的演讲提纲 同学们,今天我演讲的主题是:……
- “再长的路,一步步也能走完;再短的路,不迈开双脚也无法到达。”从哲学上看,这是因为( ) A.事物发展的方向是前进上
- 如图所示,一半径r = 0.2m的1/4光滑圆弧形槽底端B与水平传带相接,传送带的运行速度为v0=4m/s,长为L=1.



