高中 数学
集合U,M,N,P如图所示,则图中阴影部分所表示的集合是( )

A . M∩(N∪P)
B . M∩∁U(N∪P)
C . M∪∁U(N∩P)
D . M∪∁U(N∪P)
已知 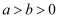 ,函数
,函数 
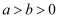 ,函数
,函数 
-
(1) 若
 ,
,  ,求不等式
,求不等式  的解集﹔
的解集﹔
-
(2) 求证:
 .
.
若椭圆 的弦
的弦 恰好被点
恰好被点 平分,则
平分,则 所在的直线方程为( )
所在的直线方程为( )
 的弦
的弦 恰好被点
恰好被点 平分,则
平分,则 所在的直线方程为( )
所在的直线方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,椭圆  的离心率为
的离心率为  ,以椭圆
,以椭圆  的上顶点
的上顶点  为圆心作圆
为圆心作圆  ,圆
,圆  与椭圆
与椭圆  在第一象限交于点
在第一象限交于点  ,在第二象限交于点
,在第二象限交于点  .
.
 的离心率为
的离心率为  ,以椭圆
,以椭圆  的上顶点
的上顶点  为圆心作圆
为圆心作圆  ,圆
,圆  与椭圆
与椭圆  在第一象限交于点
在第一象限交于点  ,在第二象限交于点
,在第二象限交于点  .
. 
(Ⅰ)求椭圆  的方程;
的方程;
(Ⅱ)求  的最小值,并求出此时圆
的最小值,并求出此时圆  的方程;
的方程;
(Ⅲ)设点  是椭圆
是椭圆  上异于
上异于  ,
,  的一点,且直线
的一点,且直线  ,
,  分别与
分别与  轴交于点
轴交于点  ,
,  ,
,  的坐标原点,求证:
的坐标原点,求证:  为定值.
为定值.
在  中,内角
中,内角  ,
,  ,
,  对边的边长分别是
对边的边长分别是  ,
,  ,
,  .已知
.已知  .
.
 中,内角
中,内角  ,
,  ,
,  对边的边长分别是
对边的边长分别是  ,
,  ,
,  .已知
.已知  .
.
-
(1) 求角
 的大小;
的大小;
-
(2) 若
 ,
,  ,求
,求  的值.
的值.
若在区间  上,函数
上,函数  的最小值不小于
的最小值不小于  的最大值,则m的取值可能为( )
的最大值,则m的取值可能为( )
 上,函数
上,函数  的最小值不小于
的最小值不小于  的最大值,则m的取值可能为( )
的最大值,则m的取值可能为( )
A . -2
B . 0
C . 5
D . 6
已知  ,
,  ,
,  ,则
,则 

 ,
,  ,
,  ,则
,则 

A .  B .
B .  C .
C .  D .
D . 
已知向量  ,
,  满足
满足  ,
,  ,若
,若  ,则
,则  与
与  的夹角为.
的夹角为.
 ,
,  满足
满足  ,
,  ,若
,若  ,则
,则  与
与  的夹角为.
的夹角为.
已知函数  是奇函数,
是奇函数,  为偶函数,
为偶函数,  且(e是自然对数的底数).
且(e是自然对数的底数).
 是奇函数,
是奇函数,  为偶函数,
为偶函数,  且(e是自然对数的底数).
且(e是自然对数的底数).
-
(1) 分别求出
 和
和  的解析式;
的解析式;
-
(2) 记
 ,请判断
,请判断  的奇偶性和单调性,并分别说明理由;
的奇偶性和单调性,并分别说明理由;
-
(3) 若存在
 ,使得不等式
,使得不等式  能成立,求实数m的取值范围.
能成立,求实数m的取值范围.
已知A={x|x=3k﹣1,k∈Z},则下列表示正确的是( )
A . ﹣1∉A
B . ﹣11∈A
C . 3k2﹣1∈A
D . ﹣34∉A
已知 ,
,  是单位向量,且
是单位向量,且 , 向量
, 向量 是与
是与 同向的单位向量,则向量
同向的单位向量,则向量 在
在 上的投影向量为( )
上的投影向量为( )
 ,
,  是单位向量,且
是单位向量,且 , 向量
, 向量 是与
是与 同向的单位向量,则向量
同向的单位向量,则向量 在
在 上的投影向量为( )
上的投影向量为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  在点
在点  处的切线方程是( )
处的切线方程是( )
 在点
在点  处的切线方程是( )
处的切线方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  的部分图象如图所示,则( )
的部分图象如图所示,则( )
 的部分图象如图所示,则( )
的部分图象如图所示,则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
不等式|1﹣2x|<3的解集是 ( )
A . {x|x<1}
B . {x|﹣1<x<2}
C . {x|x>2}
D . {x|x<﹣1或x>2}
中心在原点、焦点在x轴上的椭圆与双曲线有公共焦点,左右焦点分别为  、
、  ,且它们在第一象限的交点为
,且它们在第一象限的交点为  ,
,  是以
是以  为底边的等腰三角形.若
为底边的等腰三角形.若  ,双曲线离心率的取值范围为
,双曲线离心率的取值范围为  ,则椭圆离心率的取值范围是.
,则椭圆离心率的取值范围是.
 、
、  ,且它们在第一象限的交点为
,且它们在第一象限的交点为  ,
,  是以
是以  为底边的等腰三角形.若
为底边的等腰三角形.若  ,双曲线离心率的取值范围为
,双曲线离心率的取值范围为  ,则椭圆离心率的取值范围是.
,则椭圆离心率的取值范围是. 
下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形的内角![]() 和是180°,归纳出所有三角形的内角和都是180°;
和是180°,归纳出所有三角形的内角和都是180°;
③张军某次考试成绩是100分,由此推出全班同学的成绩都是100分;
④三角形内角和是180°,四边形内角和是360°,五边形内角和是540°,由此得凸n边形内角和是(n-2)·180°.
A.①② B.①③ C.①②④ D.②④
已知![]() ,则
,则![]() 的共轭复数
的共轭复数![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
设![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
已知圆![]() 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线![]() 相切.
相切.
(1)求直线![]() 被圆C所截得的弦AB的长;
被圆C所截得的弦AB的长;
(2)过点![]() 作两条与圆
作两条与圆![]() 相切的直线,切点分别为
相切的直线,切点分别为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若与直线![]() 垂直的直线
垂直的直线![]() 不过点
不过点![]() ,且与圆C交于不同的两点
,且与圆C交于不同的两点![]() .若
.若![]() 为钝角,求直线
为钝角,求直线![]() 的纵截距的取值范围.
的纵截距的取值范围.
最近更新
- (2013重庆市冲刺卷)设某人造卫星绕地球做匀速圆周运动,轨道半径为r。已知地球的质量为M,万有引力常量为G,该人造卫星
- 阅读下面的文言文,完成9~12题。 柳宗元 王叔文之党坐谪官者,凡十年不量移,执政有怜其才欲渐进之者,悉召至京师。谏官争
- 《汽化和液化》中考试题(21.(2003·福州市)在“观察水的沸腾”的实验中,如图所示. (1)本实验目的是:观察水
- Tom and Mike were good friends. 1 , sometimes they were
- 以速度v0水平抛出一小球,如果从抛出到某时刻小球的竖直分位移与水平分位移大小相等,以下判断正确的是( )
- 下图是1949年以来中国新增建交国数示意图。其中建交国数量最多时的主要原因是 A..新中国在万隆会议上赢得尊重
- 下列国家中两次社会性质的变化都是通过改革而完成的是( ) A.日本 B.美国
- 下面为“1981年8月27日20时生成的热带气旋中心位置及其移动路径图”,和反映该天气系统强度演变过程的中心海平面气压值
- I lost my way in complete darkness and, ____ matters worse,
- 区域产业竞争力系数表示该区域某产业的输出额占一定区域市场的比重,产业竞争力系数越大,产业竞争力也就越强。产业竞争力系数可
- 函数,若,则的取值范围是__________________。
- 20世纪50年代中期到70年代初,日本经济持续高速发展。其原因有①美国的扶持 ②制定适当的经济政策 ③引进最新的科技成就
- 已知△ABC内接于抛物线y2=16x,其中A(1,4),且△ABC的重心为抛物线的焦点,求直线BC的方程.
- 已知等差数列{ }中,,,则的值是() A. 15 B. 30 C. 31
- 自行车在我国是很普及的代步工具,从自行车的结构和使用上来看,它涉及了许多物理知识,对其认识错误的是( )A.坐垫呈马
- 提高效率,促进公平,是经济学家和社会学家讨论的永恒话题。关于效率与公平,下列说法中合理的是 A.基于公平原则,个税征缴应
- 寒山转苍翠,_______________。倚仗柴门外,临风听暮蝉。(王维《辋川闲居赠裴秀才迪》)
- 将纯锌片和纯铜片按图示方式插入同浓度的稀硫酸中一段时间,以下叙述正确的是A.两烧杯中铜片表面均无气泡产生 B.甲中铜片是
- Some people worry about being the target of laughter. These
- 如图所示,在足够高的竖直墙面上A点,以水平速度v0向左抛出一个质量为m的小球,小球抛出后始终受到水平向右的恒定风力的作用



