高中 数学
 ,且
,且  ,则实数
,则实数  的取值范围为( )
的取值范围为( )
 B .
B .  C .
C .  D .
D . 
 与
与  轴相切于点
轴相切于点  ,与
,与  轴的正半轴交于
轴的正半轴交于  两点,且
两点,且  ,求圆
,求圆  的标准方程
的标准方程
 ,下面4个判断错误的有( )
,下面4个判断错误的有( ) ①函数  的图象是中心对称图形;②函数
的图象是中心对称图形;②函数  的图象是轴对称图形;③函数
的图象是轴对称图形;③函数  在
在  单调递增;④函数
单调递增;④函数  在
在  单调递减;
单调递减;
 的图象上的相异两点,若点A,B到直线
的图象上的相异两点,若点A,B到直线  的距离相等,则点A,B的横坐标之和的取值范围是( )
的距离相等,则点A,B的横坐标之和的取值范围是( )
某学校社团为了解进园旅客的具体情形以及采集旅客对园区的建议,特别在2017年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)
年龄 | 频数 | 频率 | 男 | 女 |
[0,10) | 10 | 0.1 | 5 | 5 |
[10,20) | ① | ② | ③ | ④ |
[20,30) | 25 | 0.25 | 12 | 13 |
[30,40) | 20 | 0.2 | 10 | 10 |
[40,50) | 10 | 0.1 | 6 | 4 |
[50,60) | 10 | 0.1 | 3 | 7 |
[60,70) | 5 | 0.05 | 1 | 4 |
[70,80) | 3 | 0.03 | 1 | 2 |
[80,90) | 2 | 0.02 | 0 | 2 |
合计 | 100 | 1.00 | 45 | 55 |

-
(1) 完成表格一中的空位①﹣④,并在答题卡中补全频率分布直方图,并估计2017年4月1日当日接待游客中30岁以下人数.
-
(2) 完成表格二,并问你能否有97.5%的把握认为在观花游客中“年龄达到50岁以上”与“性别”相关?
-
(3) 按分层抽样(分50岁以上与50以下两层)抽取被调查的100位游客中的10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)的人数为ξ,求ξ的分布列
(表二)
50岁以上
50岁以下
合计
男生
5
40
45
女生
15
40
55
合计
20
80
100
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:k2=
 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
 上的奇函数
上的奇函数 满足
满足 , 且在区间
, 且在区间 上单调递增,则( )
上单调递增,则( )
 B .
B .  C .
C .  D .
D . 
 B . m>
B . m> C . m<0
D . m≤
C . m<0
D . m≤
 ,
,  ,则
,则  等于( )
等于( )
 B .
B . 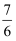 C .
C . 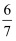 D .
D . 
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为  ,且各次投篮互不影响.
,且各次投篮互不影响.
-
(1) 求甲乙各投球一次,比赛结束的概率;
-
(2) 求甲获胜的概率.
 的叙述中正确的有( )
的叙述中正确的有( )
 是函数f(x)的最靠近y轴的一条对称轴,则
是函数f(x)的最靠近y轴的一条对称轴,则 C . 若
C . 若 , 则点(
, 则点(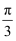 , 0)是函数f(x)的一个对称点
D . 若函数f(x)在区间[0,π]上有两个零点,则
, 0)是函数f(x)的一个对称点
D . 若函数f(x)在区间[0,π]上有两个零点,则
 的展开式中
的展开式中  的系数为( )
的系数为( )
 )上是减函数的是( )
)上是减函数的是( )

 的前n项和为
的前n项和为  ,
,  且
且  ,当
,当  取最大值时,n的值为( )
取最大值时,n的值为( )

-
(1) 根据表中数据建立年销售量y关于年宣传费x的回归方程;
-
(2) 已知这种产品的年利润z与x,y的关系为
 ,根据(1)中的结果回答下列问题:
,根据(1)中的结果回答下列问题: ①当年宣传费为10万元时,年销售量及年利润的预报值是多少?
②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.
附:回归方程
 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为
参考数据:
 .
.
 .
. (1)求f(x)的解析式
(2)若常数m>0,求函数f(x)在区间[﹣m,m]上的最大值.

已知不等式![]() .
.
(1)若![]() ,求不等式的解集;
,求不等式的解集;
(2)若已知不等式的解集不是空集,求![]() 的取值范围.
的取值范围.
抛物线![]() 的焦点为
的焦点为![]() ,斜率为正的直线
,斜率为正的直线![]() 过点
过点![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,满足
两点,满足![]() .
.
(1)求直线![]() 的斜率;
的斜率;
(2)过焦点![]() 与
与![]() 垂直的直线交抛物线于
垂直的直线交抛物线于![]() 两点,求四边形
两点,求四边形![]() 的面积.
的面积.
已知O为坐标原点,△AOB中,边OA所在的直线方程是![]() ,边AB所在的直线方程是
,边AB所在的直线方程是![]() ,且顶点B的横坐标为6。
,且顶点B的横坐标为6。
(1)求△AOB中,与边AB平行的中位线所在直线的方程;
(2)求△AOB的面积;
(3)已知OB上有点D,满足△AOD与△A![]() BD的面积
BD的面积![]() 比为2,求AD所在的直线方程。
比为2,求AD所在的直线方程。
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将
△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD。
(1)求证:AB⊥DE;
(2)若点F为BE的中点,求直线AF与平面ADE所成角正弦值。

A. 2 B. -2 C. 4 D. -4
- 2013年,央视节目《中国汉字听写大会》在周末黄金时间播出,其宣传语是“书写的文明传递,民族的未雨绸缪”。与汉字一脉相承
- 具有“国宝”称号,并为我国所特有的珍惜哺乳动物是 A. 白鳍豚 B. 金丝猴 C. 大熊猫 D. 扬子鳄
- (6分)某种金属板M受到某种紫外线照射时会不停地发射电子,射出的电子具有不同的方向,其速度大小也不相同.在M旁放置一个金
- –Sorry! I’m busy today. I can’t go swimming with you. --____
- 读长江干流及南北向铁路干线示意图,衡山、峨眉山、庐山、武陵源分别位于图中铁路沿线的顺序是( ) A.②③④①
- 已知向量.令, (1)求的最小正周期; (2)当时,求的最小值以及取得最小值时的值.
- 下列词语中,各对加点字的读音都不相同的一项是( ) A、背负/背井离乡 模样/模棱两可 调动/调
- 已知直线与曲线相切,则的值为( ) A.1 B. 2
- 下列不属于化合反应,但属于氧化反应的是( ) A.红磷在空气中燃烧 B. 酒精在空气
- 四位同学在体育测试时各准备了一些补充能量的食物,甲准备了一些水果,乙准备了一些牛肉干,丙准备了一些糖,丁准备了一些牛奶。
- 蹦床比赛时,从接触蹦床到运动到最低点的过程中,运动员的( ) A.动能增大 B.动能转
- Mr Smith, _________ of the ___________speech, started to rea
- 万金油的主要成分是薄荷脑(C10H10O),下列关于薄荷脑的说法错误的是( ) A.属于有机物B.由碳、氢、氧三种元
- 4.下列各句中,没有语病的一项是( ) A.当今的环境保护技术不仅做到了生产过程不浪费资源,不污染环境,保证产品
- 英国君主立宪制确立的标志是下列哪一法律文献的通过( ) A.《神学政治论》 B.《政府论》 C.《独立宣言》 D
- 只含有碳、氢或碳、氢、氧的物质充分燃烧后的产物均为CO2和H2O.相同分子数目的①C2H5OH②CH3OH ③CH4④C
- 原产地在非洲的经济作物是( ) A、咖啡、橄榄、油棕、香蕉 B、水稻、花生、可可、芝麻 C
- 穿越时光隧道来到宋代,下面哪些社会风貌是可以看到的( ) ① 在当时商业都市里你可以看到琳琅满目的商品,其中就
- (本小题满分12分)在数学研究性学习活动中,某小组要测量河对面和两个建筑物的距离,作图如下,所测得的数据为米,,,,,请
- 如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求:直径AB的长



