高中 数学
已知两条直线m,n,两个平面 ,
,  , 给出下面四个命题:
, 给出下面四个命题:
① , 或者m,n相交
, 或者m,n相交
② ∥
∥ ,
,  ,
, 

③m∥n,m∥
 n∥
n∥
④ , m∥n
, m∥n n∥
n∥ 或者n∥
或者n∥
其中正确命题的序号是( )
 ,
,  , 给出下面四个命题:
, 给出下面四个命题:①
 , 或者m,n相交
, 或者m,n相交②
 ∥
∥ ,
,  ,
, 

③m∥n,m∥

 n∥
n∥
④
 , m∥n
, m∥n n∥
n∥ 或者n∥
或者n∥
其中正确命题的序号是( )
A . ①③
B . ②④
C . ①④
D . ②③
对某商店一个月内(按30天计)每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )
A . 47,45,56
B . 46,45,53
C . 46,45,56
D . 45,47,53
已知x,y满足不等式组  ,则z=2y﹣x的最大值为.
,则z=2y﹣x的最大值为.
 ,则z=2y﹣x的最大值为.
,则z=2y﹣x的最大值为.
已知扇形的圆心角为60°,所在圆的半径为10cm,则扇形的面积是 cm2 .
用乘法原理求出(a+b+c)5的项数.
已知函数  是偶函数
是偶函数
 是偶函数
是偶函数
-
(1) 求实数
 的值;
的值;
-
(2) 若函数
 没有零点,求实数
没有零点,求实数  的取值范围
的取值范围
-
(3) 若函数
 ,
,  的最大值为0,求实数
的最大值为0,求实数  的值.
的值.
已知双曲线  =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0).
 =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0).
-
(1) 若双曲线的一条渐近线方程为y=x且c=2,求双曲线的方程;
-
(2) 以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过A作圆的切线,斜率为﹣
 ,求双曲线的离心率.
,求双曲线的离心率.
已知⊙C:x2+y2﹣2x+my﹣4=0上有两点M、N关于2x+y=0对称,直线l:λx+y﹣λ+1=0与⊙C相交于A、B,则|AB|的最小值为.
“费马点”是由十七世纪法国业余数学家之王费马提出并征解的一个问题,该问题是指在位于三角形内找一个到三角形三个顶点距离之和最小的点.由当时意大利数学家托里拆利给出解答,当三角形三个内角均小于 时,“费马点”与三个顶点的连线正好三等分“费马点”所在的周角,即该点所对的三角形三边的张角相等且均为
时,“费马点”与三个顶点的连线正好三等分“费马点”所在的周角,即该点所对的三角形三边的张角相等且均为 ;当三角形有一内角大于或等于
;当三角形有一内角大于或等于 时,所求点为三角形最大内角的顶点.在
时,所求点为三角形最大内角的顶点.在 中,
中, 、
、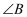 、
、 的对边分别为a、b、c,且
的对边分别为a、b、c,且 ,
,  ,
,  成等差数列,
成等差数列, .
.
 时,“费马点”与三个顶点的连线正好三等分“费马点”所在的周角,即该点所对的三角形三边的张角相等且均为
时,“费马点”与三个顶点的连线正好三等分“费马点”所在的周角,即该点所对的三角形三边的张角相等且均为 ;当三角形有一内角大于或等于
;当三角形有一内角大于或等于 时,所求点为三角形最大内角的顶点.在
时,所求点为三角形最大内角的顶点.在 中,
中, 、
、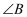 、
、 的对边分别为a、b、c,且
的对边分别为a、b、c,且 ,
,  ,
,  成等差数列,
成等差数列, .
.
-
(1) 证明:
 是直角三角形;
是直角三角形;
-
(2) 若O是
 的“费马点”,
的“费马点”, .设
.设 ,
,  ,
,  , 求
, 求 的值.
的值.
定义在  上的奇函数
上的奇函数  ,对于
,对于  ,都有
,都有  ,且满足
,且满足  ,
,  ,则实数取值范围是( )
,则实数取值范围是( )
 上的奇函数
上的奇函数  ,对于
,对于  ,都有
,都有  ,且满足
,且满足  ,
,  ,则实数取值范围是( )
,则实数取值范围是( )
A .  或
或  B .
B .  C .
C .  或
或  D .
D . 
 或
或  B .
B .  C .
C .  或
或  D .
D . 
甲、乙、丙三人各买了一辆不同品牌的新汽车,汽车的品牌为奇瑞、传祺、吉利.甲、乙、丙让丁猜他们三人各买的什么品牌的车,丁说:“甲买的是奇瑞,乙买的不是奇瑞,丙买的不是吉利.”若丁的猜测只对了一个,则甲、乙所买汽车的品牌分别是( )
A . 吉利,奇瑞
B . 吉利,传祺
C . 奇瑞,吉利
D . 奇瑞,传祺
甲乙丙三人参加2022年冬奥会北京、延庆、张家口三个赛区志愿服务活动,若每人只能选择一个赛区,且选择其中任何一个赛区是等可能的.记X为三人选中的赛区个数,Y为三人没有选中的赛区个数,则( )
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
“  成立”是“
成立”是“  成立”的( )
成立”的( )
 成立”是“
成立”是“  成立”的( )
成立”的( )
A . 充分不必要条件
B . 必要不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
 ( ).
( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  是定义在
是定义在  上的奇函数,且当
上的奇函数,且当  时,
时,  ,
,
 是定义在
是定义在  上的奇函数,且当
上的奇函数,且当  时,
时,  ,
,
-
(1) 求
 在
在  上的解析式;
上的解析式;
-
(2) 求
 在
在  上的值域;
上的值域;
-
(3) 求
 的值.
的值.
已知向量  ,
,  ,若
,若 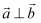 ,则实数
,则实数  的值为( )
的值为( )
 ,
,  ,若
,若 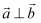 ,则实数
,则实数  的值为( )
的值为( )
A . -2
B .  C .
C .  D . 2
D . 2
 C .
C .  D . 2
D . 2
若函数  的解析式为
的解析式为  ,则
,则  .
.
 的解析式为
的解析式为  ,则
,则  .
.
设 , 则( )
, 则( )
 , 则( )
, 则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如下图所示):
(1)该算法使用什么类型的循环结构;
(2)图中①处和②处应填上什么语句,使之能完成该题算法功能;
(3)根据程序框图写出程序。

已知函数![]() ,若在区间
,若在区间![]() 上随机取一点
上随机取一点![]() ,则使得
,则使得![]() 的概率为 ▲ .
的概率为 ▲ .
最近更新
- Imagine a mass of floating waste is two times the size of th
- 标准状况下二氧化碳是一种_______、_______、密度比空气_______、_______溶于水的气体。加大压强、
- 下图是近年来出现的国外种植返销国内模式,对这一模式认识正确的是( ) ①参与经济全球化就能够推动经济发展 ②经济发展
- Competition. It’s a simple word, yeta very complex word that
- _______ that Marie was able to set up new branches elsewhere
- 某手机网站反复弹出广告:“发送短信,告知生辰八字,可洞晓您的姻缘”“大师指点靓名,让您小孩幸福一生”……,等等。诸如此类
- 在下面横线处填写相关诗文。(8分,每空2分) (1)我寄愁心与明月, 。(《闻王昌龄左迁龙标遥有此寄
- 科学家将两种元素(铅和氪)的原子对撞,获得一种质子数为118,中子数为175的超重元素,该元素的原子核内的中子数与核外电
- His test results are not very consistent (一致的). He does well
- 直到康乾盛世,中国的小农经济历经千年发展到了辉煌的顶峰,中国的GDP在晚清甚至达到了当时世界的三分之一,然而著名历史学家
- 在高能物理研究中,粒子回旋加速器起着重要作用,如图甲为它的示意图。它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条
- 下列各句中,加点词语使用正确的一句是( )A.阳春三月,一位老人在杭州西湖岸边展示他高超的拳脚功夫,引来许多行人侧目观赏
- 下列关于动、植物结构层次的叙述正确的是( ) A.动、植物的结构层次均为:细胞 组织 器官 系统生物体
- 敲 雪 ①睡到半夜,忽然觉得好冷。也许,外面下雪了。我想。我
- 下列词语中加点的字,读音有错误的一组是A.炽情(chì) 霎时(chà) 纤维(xiān) 锃光瓦亮(zèng)
- NEMS NEWRIEnvironmental Master of ScienceNEWRI: NanyangEnvir
- 下列消费行为中属于适度消费的是
- 找出没有语病的一项 ( )A.我国目前的测控通信网,是我国航天史上规模最庞大、技术最先进、可靠性更高的系统。B.北京时间
- 阅读下面的文章,完成下面试题。 牛的写意 李汉荣 ①
- 读某日某时海平面天气图(下图,单位:百帕),回答下图中,此时可能出现降水天气的地区是A.山东半岛 B.长江三角洲



