高中 数学
设点P是直线  上的动点,过点P引圆
上的动点,过点P引圆  的切线
的切线  (切点为
(切点为  ),若
),若  的最大值为
的最大值为  ,则该圆的半径r等于.
,则该圆的半径r等于.
 上的动点,过点P引圆
上的动点,过点P引圆  的切线
的切线  (切点为
(切点为  ),若
),若  的最大值为
的最大值为  ,则该圆的半径r等于.
,则该圆的半径r等于.
设  为奇函数,则
为奇函数,则  .
.
 为奇函数,则
为奇函数,则  .
.
下列各组函数是同一函数的是( )
A . f(x)=x-1, g(x)=( 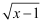 )2
B . f(x)=|x-1|, g(x)=
)2
B . f(x)=|x-1|, g(x)=  C .
C .  ,
,  D . f(x)=
D . f(x)=  ,
, 
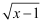 )2
B . f(x)=|x-1|, g(x)=
)2
B . f(x)=|x-1|, g(x)=  C .
C .  ,
,  D . f(x)=
D . f(x)=  ,
, 
“关于x的不等式 对于一切实数x都成立”是“
对于一切实数x都成立”是“ ”的( )
”的( )
 对于一切实数x都成立”是“
对于一切实数x都成立”是“ ”的( )
”的( )
A . 充要条件
B . 充分非必要条件
C . 必要非充分条件
D . 既非充分又非必要条件
如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,AC=4,BD=2,且侧棱AA1=3.其中O1为A1C1与B1D1的交点.

-
(1) 求点B1到平面D1AC的距离;
-
(2) 在线段BO1上,是否存在一个点P,使得直线AP与CD1垂直?若存在,求出线段BP的长;若不存在,请说明理由.
已知m∈R,命题p:对任意x∈[0,1],不等式2x﹣2≥m2﹣3m 恒成立;命题q:存在x∈[﹣1,1],使得m≤ax 成立.
-
(1) 若p为真命题,求m 的取值范围;
-
(2) 当a=1 时,若p且q为假,p或q为真,求m的取值范围.
设定义在区间(﹣b,b)上的函数f(x)=lg 是奇函数(a,b∈R,且a≠﹣2),则ab的取值范围是( )
是奇函数(a,b∈R,且a≠﹣2),则ab的取值范围是( )
 是奇函数(a,b∈R,且a≠﹣2),则ab的取值范围是( )
是奇函数(a,b∈R,且a≠﹣2),则ab的取值范围是( )
A . (1, ]
B . (0,
]
B . (0, ]
C . (1,
]
C . (1, )
D . (0,
)
D . (0, )
)
 ]
B . (0,
]
B . (0, ]
C . (1,
]
C . (1, )
D . (0,
)
D . (0, )
)
已知  的二项展开式中,所有二项式系数之和为1024.
的二项展开式中,所有二项式系数之和为1024.
 的二项展开式中,所有二项式系数之和为1024.
的二项展开式中,所有二项式系数之和为1024.
-
(1) 求n的值,并求展开式所有项的系数之和;
-
(2) 写出展开式中所有x的整数次幂的项.
下列是  成立的一个充分不必要条件的是( )
成立的一个充分不必要条件的是( )
 成立的一个充分不必要条件的是( )
成立的一个充分不必要条件的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
数 f(x)=x2 在点 (2,f(2))处的切线方程为( )
A . y=4
B . y=4x+4
C . y=4x+2
D . y=4x-4
在湖边,我们常看到成排的石柱子之间两两连以铁链,这就是悬链线(Catenary),其形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名.选择适当的坐标系后,悬链线的方程是一个双曲余弦函数  ,其中a为非零常数,在此坐标平面上,过原点的直线与悬链线相切于点
,其中a为非零常数,在此坐标平面上,过原点的直线与悬链线相切于点  ,则
,则  的值可能为( )(注:
的值可能为( )(注:  表示不大于x的最大整数)
表示不大于x的最大整数)
 ,其中a为非零常数,在此坐标平面上,过原点的直线与悬链线相切于点
,其中a为非零常数,在此坐标平面上,过原点的直线与悬链线相切于点  ,则
,则  的值可能为( )(注:
的值可能为( )(注:  表示不大于x的最大整数)
表示不大于x的最大整数) 
A . -2
B . -1
C . 1
D . 2
已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是( )
A . 3cm
B . 26cm
C . 24cm
D . 65cm
已知奇函数  是定义在
是定义在  上的单调函数,若正实数
上的单调函数,若正实数  ,
,  满足
满足  则
则  的最小值是( )
的最小值是( )
 是定义在
是定义在  上的单调函数,若正实数
上的单调函数,若正实数  ,
,  满足
满足  则
则  的最小值是( )
的最小值是( )
A .  B .
B .  C . 2
D . 4
C . 2
D . 4
 B .
B .  C . 2
D . 4
C . 2
D . 4
已知函数  ,若
,若  ,则x的取值范围是.
,则x的取值范围是.
 ,若
,若  ,则x的取值范围是.
,则x的取值范围是.
与圆x2+(y﹣2)2=2相切,且在两坐标轴上的截距相等的直线方程为
已知扇形的半径为9,圆心角为120°,则扇形的弧长为,面积为.
如图所示,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 为侧棱
为侧棱 上靠近
上靠近 的三等分点,
的三等分点, 底面
底面 , 且
, 且 .
.
 中,底面
中,底面 为正方形,
为正方形, 为侧棱
为侧棱 上靠近
上靠近 的三等分点,
的三等分点, 底面
底面 , 且
, 且 .
.
-
(1) 在侧棱
 上是否存在点
上是否存在点 , 使得点
, 使得点 四点共面?若存在,指出点
四点共面?若存在,指出点 的位置,并证明;若不存在,请说明理由;
的位置,并证明;若不存在,请说明理由;
-
(2) 求二面角
 的余弦值.
的余弦值.
已知动圆过定点 



的直线与轨迹

在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)若![]() 为曲线
为曲线![]() ,
,![]() 的公共点,求直线
的公共点,求直线![]() 的斜率;
的斜率;
(Ⅱ)若![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,当
上的动点,当![]() 取最大值时,求
取最大值时,求![]() 的面积.
的面积.
sin2(π+α)-cos(π+α)cos(-α)+1的值为( )
A.1 B.2sin2α C.0 D.2
最近更新
- 海水经过晒盐后得到粗盐和苦卤,重结晶后的食盐中还含有硫酸钠、氯化镁、氯化钙等可溶性杂质,他们在溶液中主要以SO42-、C
- 读图,回答下面试题。关于该图反映的大气运动的叙述正确的是 A.只有水平气压梯度力作用 B.高空 C.不考虑摩擦力 D
- 下列实验中,对应的现象以及结论都正确且两者具有因果关系的是
- 股票与债券的相同点是( ) A.都可以上市流通 B.收益是一样的 C.到期都还本付息
- I learned to play on a pianopurchased at Grinnell Brothers i
- 比较下列各对数的大小. 与;
- 2010年2月27日,中共中央政治局常委、国务院总理温家宝在接受中国政府网、新华网联合专访,与广大网友在线交流时指出:“
- 下图中甲图是一盆栽植物,乙图表示该植物不同器官对不同浓度的生长素的反应。据图回答下列问题:(1)乙图中
- 在等差数列中,,.令,数列的前项和为. (1)求数列的通项公式; (2)求数列的前项和; (3)是否存在正整数,(),使
- — Is your father a doctor in No.2Hospital? —No, he _________
- 下列有关生物体内水的叙述,错误的是 ①参与运输营养物质和代谢废物的水是自由水 ②生物体内化学反应离不开水 ③水是细胞结构
- (2013•怀化)下列属于我国特有珍稀植物的是()A. 银杉 B. 桃树 C. 毛竹 D. 杨梅
- 函数=的最小正周期是 A. B.2
- 明太祖朱元璋废除丞相,主要是由于( ) A.元朝丞相贪婪暴戾,扰乱朝纲 B.丞相大多平庸无能,败坏
- 港澳和珠江三角洲地区相比,港澳的优势是( ) A.廉价的劳动力B.土地资源 C.先进的技术和管理经验D.矿产资源
- 下面语句中加点的成语,使用恰当的一项是( )A.进入岳麓山,古木参天,云雾缭绕,极目远眺,翠竹林海,
- 如图所示, 在倾角为θ的光滑斜面上放有两块小木块,劲度系数为k1的轻质弹簧两端分别与质量为m1和m2的物块1、2拴接,
- —Let's watch TV.—______. A.Sorry,I don't
- 完成下面两道综合性学习题 (1)湖南省第十二届运动会将于今年9月在 娄底举行。红山学校九年级5班的同学们积极参与筹备委员
- 玉米子粒中黄色对无色为显性。用无色玉米作母本,去雄后授以黄色玉米花粉,若母本植株所结子粒中出现无色子粒,原因可能是



