高中 数学
 为左右焦点,
为左右焦点, 为短轴端点,长轴长为4,焦距为
为短轴端点,长轴长为4,焦距为 , 且
, 且 ,
,  的面积为
的面积为 .
.
(Ⅰ)求椭圆 的方程
的方程
(Ⅱ)设动直线 椭圆
椭圆 有且仅有一个公共点
有且仅有一个公共点 , 且与直线
, 且与直线 相交于点
相交于点 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点 , 使得以
, 使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在求出点
?若存在求出点 的坐标,若不存在.请说明理由.
的坐标,若不存在.请说明理由.
 :
:  经过两点
经过两点  ,
,  .
. (Ⅰ)求椭圆  的标准方程;
的标准方程;
(Ⅱ)过椭圆的右焦点  的直线
的直线  交椭圆
交椭圆  于
于  ,
,  两点,且直线
两点,且直线  与以线段
与以线段  为直径的圆交于另一点
为直径的圆交于另一点  (异于点
(异于点  ),若
),若  ,求直线
,求直线  的斜率.
的斜率.
 外接圆的半径为1,圆心为O.且
外接圆的半径为1,圆心为O.且 , 则
, 则 等于( )
等于( )
 B .
B .  C .
C . 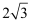 D . 3
D . 3
 D . ﹣
D . ﹣ 
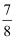 ,SA与圆锥底面所成角为45°。若△SAB的面积为
,SA与圆锥底面所成角为45°。若△SAB的面积为  ,则圆锥的侧面积为。
,则圆锥的侧面积为。
 .
.
-
(1) 求sinB的值;
-
(2) 若D为AC的中点,且BD=1,求△ABD面积的最大值.
 的部分图像为( )
的部分图像为( )
 B .
B .  C .
C .  D .
D . 

 可以用如下方法定义:
可以用如下方法定义: ,
,  , 则
, 则 是数列
是数列 的第几项?( )
的第几项?( )
 =(sinx,1),
=(sinx,1),  =(
=(  Acosx,
Acosx,  cos2x)(A>0),函数f(x)=
cos2x)(A>0),函数f(x)=  •
•  的最大值为6.
的最大值为6.
-
(1) 求A;
-
(2) 将函数y=f(x)的图象像左平移
 个单位,再将所得图象各点的横坐标缩短为原来的
个单位,再将所得图象各点的横坐标缩短为原来的  倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,  ]上的值域.
]上的值域.

-
(1) 求证:直线BD1∥平面PAC;
-
(2) 求证:平面PAC⊥平面BDD1B1;
-
(3) 求CP与平面BDD1B1所成的角大小.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90º,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD。
(1)若点O为线段AC的中点,求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所夹的角。
所夹的角。

已知 
” 是 “

A .充分而不必要条件 B .必要而不充分条件
C .充分必要条件 D .既不充分也不必要条件
已知定义在![]() 上的奇函数
上的奇函数![]() 和偶函数
和偶函数![]() 满足:
满足: ![]() ,则( )
,则( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
在平面四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1) 求![]() ;
;
(2) 若![]() ,求
,求![]() .
.
直角三角形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一个动点,且
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.

(1)当![]() 时,证明:
时,证明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
对两个变量x、y进行线性回归分析,计算得到相关系数r=﹣0.9962,则下列说法中正确的是( )
A.x与y正相关 B.x与y具有较强的线性相关关系
C.x与y几乎不具有线性相关关系 D.x与y的线性相关关系还需进一步确定
- 请回答下列关于人体营养和血糖、体温调节的问题。 (1)营养学家在调查素食者人群时发现,由于长期营养缺陷导致贫血病的发病率
- 工业上通常用工业酒精和生石灰混合蒸馏法制取无水乙醇。如图是实验室中模拟工业原理制取无水乙醇的装置。 回答下列问题: (1
- 在等比数列{an}中,,则首项a1=( )A. B.
- 下列叙述正确的是 A.狗的白毛与黑毛,兔的长毛与卷毛都是相对性状 B.基因型相同,表现型一定相同;表现型
- 在直角坐标系中,正比例函数y=kx(k≠0)中,k<0,则其图象可能是( )
- 阅读温庭筠的《菩萨蛮》一词,完成下列题目。 小山①重叠②金③明灭,鬓云欲度香腮雪。懒起画蛾眉,弄妆梳洗迟。
- 分别选出下列各题中对文言句子的翻译有误的一项。 A.夫夷以近,则游者众。(平坦而又近的地方,前来游览的人便多。) B.有
- He is not _____ professional. He plays _____ pianojust for
- ㈠阅读下面一首诗,完成小题。(4分)(一)《村晚》(4分)草满池塘水满陂①,山衔落日浸寒漪②。牧童归去横牛背,短笛无腔③
- 下图是某生态系统食物网简图,请据图回答:(1)该食物网中数量最多的生物是 (1) ;如果该系统中喷洒了含有有机汞
- 6.下列各项中,加点词解释有错误的一项是 A. 原庄宗之所以得天下(推究) 系燕父子以组(缚)
- 体积为1×10-3m3的物体浸没在水中,物体受到的浮力为_______N,若物体受到的浮力与重力的合力为20N,则物体的
- 顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形满足条件的是() ①平行四边形;②菱形;③对角线互相垂直的四边
- 下列词语中没有错别字的一项是 A. 端倪 砥砺 给予 加官晋爵 B. 分外 恍惚 喝采
- 依托孕烯是一种激素类药物,结构如图所示。下列有关依托孕烯的说法正确的是 A.依托孕烯的分子式为C21H28O2B.依托孕
- There are many old trees in our school, each ________ about
- 如图是从平面镜中看到的钟表,则其指示的真实时刻是 ()A .1:45 B.2:57 C.9:03 D.11:15
- 南昌大学研究人员发现,用2%的小苏打漱口能有效预防口腔粘膜糜烂溃疡的发生或修复原有口腔黏膜的损伤。小苏打属于( ) A.
- 在“十二五”规划中,国家将在民族自治地方资源开发项目和基础设施建设项目中适当增加国家投资比重和政策性银行贷款比重,加大对
- 锌银电池广泛用作各种电子仪器的电源,它的充电、放电过程可表示为2Ag+Zn(OH)2Ag2O+Zn+H2O 回答下列有关



