高中 数学
若角  的终边过点
的终边过点  ,则
,则  =.
=.
 的终边过点
的终边过点  ,则
,则  =.
=.
已知 , 用单位圆求证下面的不等式:
, 用单位圆求证下面的不等式:
 , 用单位圆求证下面的不等式:
, 用单位圆求证下面的不等式:sinx<x<tanx;
设全集为  ,集合
,集合  ,
,  ,则
,则  ;
;  .
.
 ,集合
,集合  ,
,  ,则
,则  ;
;  .
.
如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形,则该多面体的各条棱中,最长的棱的长度为( )

A . 2  B .
B . 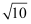 C . 2
C . 2  D .
D . 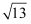
 B .
B . 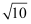 C . 2
C . 2  D .
D . 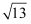
已知圆  经过坐标原点
经过坐标原点  和点
和点  ,且圆心
,且圆心  在直线
在直线  上.
上.
 经过坐标原点
经过坐标原点  和点
和点  ,且圆心
,且圆心  在直线
在直线  上.
上.
-
(1) 求圆
 的方程;
的方程;
-
(2) 设
 是圆
是圆  的两条切线,其中
的两条切线,其中  为切点.
为切点. ①若点
 在直线
在直线  上运动,求证:直线
上运动,求证:直线  经过定点;
经过定点;②若点
 在曲线
在曲线  (其中
(其中  )上运动,记直线
)上运动,记直线  与
与  轴的交点分别为
轴的交点分别为  , 求
, 求  面积的最小值.
面积的最小值.
已知直线  的斜率为
的斜率为  ,则直线
,则直线  的法向量为( )
的法向量为( )
 的斜率为
的斜率为  ,则直线
,则直线  的法向量为( )
的法向量为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知平面α∥β∥γ,两条直线l,m分别与平面α,β,γ相交于点A,B,C和D,E,F,已知AB=6,  ,则AC=.
,则AC=.
 ,则AC=.
,则AC=.
已知函数y=f(x)的定义R在上的奇函数,当x<0时f(x)=x+1,那么不等式f(x)< 的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A . [0, )
B . (-
)
B . (- ,-
,- )
) [0,
[0, )
C . (-
)
C . (- ,-
,- )
D . (-
)
D . (- ,-
,- )
) (0,
(0, )
)
 )
B . (-
)
B . (- ,-
,- )
) [0,
[0, )
C . (-
)
C . (- ,-
,- )
D . (-
)
D . (- ,-
,- )
) (0,
(0, )
)
已知函数  .
.
 .
.
-
(1) 求
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
-
(2) 若
 在区间
在区间  上的最大值与最小值的和为
上的最大值与最小值的和为  ,求
,求  的值.
的值.
在平面直角坐标系xOy中,已知直线  与圆O:
与圆O:  相切.
相切.
 与圆O:
与圆O:  相切.
相切.
-
(1) 直线l过点(2,1)且截圆O所得的弦长为
 ,求直线l的方程;
,求直线l的方程;
-
(2) 已知直线y=3与圆O交于A,B两点,P是圆上异于A,B的任意一点,且直线AP,BP与y轴相交于M,N点.判断点M、N的纵坐标之积是否为定值?若是,求出该定值;若不是,说明理由.
已知倾斜角为  的直线
的直线  过点
过点  和点
和点  ,
,  在第一象限,
在第一象限,  .
.
 的直线
的直线  过点
过点  和点
和点  ,
,  在第一象限,
在第一象限,  .
.
-
(1) 求点
 的坐标;
的坐标;
-
(2) 若直线
 与双曲线
与双曲线  :
:  相交于
相交于  、
、  两点,且线段
两点,且线段  的中点坐标为
的中点坐标为  ,求
,求  的值;
的值;
-
(3) 对于平面上任一点
 ,当点
,当点  在线段
在线段  上运动时,称
上运动时,称  的最小值为
的最小值为  与线段
与线段  的距离,已知点
的距离,已知点  在
在  轴上运动,写出点
轴上运动,写出点  到线段
到线段  的距离
的距离  关于
关于  的函数关系式.
的函数关系式.
设函数 , 若
, 若 , 则实数a的值为.
, 则实数a的值为.
 , 若
, 若 , 则实数a的值为.
, 则实数a的值为.
如果球的体积为  ,那么该球的表面积为
,那么该球的表面积为
 ,那么该球的表面积为
,那么该球的表面积为
用反证法证明“若x2﹣1=0,则x=﹣1或x=1”时,应假设
规定[x]表示不超过x的最大整数,f(x)= , 若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
, 若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
 , 若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
, 若方程f(x)=ax+1有且仅有四个实数根,则实数a的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在平面直角坐标系xOy中,已知直线l的普通方程为 , 曲线E的参数方程为
, 曲线E的参数方程为 (
(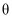 为参数).
为参数).
 , 曲线E的参数方程为
, 曲线E的参数方程为 (
(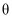 为参数).
为参数).
-
(1) 以原点O为极点,x轴正半轴为极轴建立极坐标系,求直线l及曲线E的极坐标方程;
-
(2) 若P为曲线E在第一象限上一点,射线OP按逆时针方向旋转
 ,与直线l相交于点Q,若
,与直线l相交于点Q,若 的面积为
的面积为 , 求
, 求 的值.
的值.
设等差数列 






有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是( )
A.ax+by+cz B.az+by+cx C.ay+bz+cx D.ay+bx+cz
南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为 ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为 ,则“
,则“ 相等”是“
相等”是“ 总相等”的
总相等”的

A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件

A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
已知直线 是曲线
是曲线 在点
在点 处的切线,则直线
处的切线,则直线 的方程为__________.
的方程为__________.
最近更新
- 设P是△ABC所在平面内的一点,+=2,则( ) A.+= B.+= C.+= D.++=
- 随着阳光体育运动在全国的开展,“每天锻炼一小时,健康工作50年,幸福生活一辈子。”的理念深入人心,校园里出现了可喜的变化
- (一)文言文阅读(19分) 阅读下面的文言文,完成4-7题。 何之元,庐江灊人也。之元幼好学,有才思,居丧过礼,
- 阅读下面的文言文,完成后面题目。 (李)愬,字元直,有筹略,善骑射。宪宗讨吴元济①,唐、邓节度使高霞寓既败,七月,唐邓节
- 名著填空。(共5分,每空1分) (1)《水浒》是中国第一部歌颂农民起义的长篇____体小说,作者 。小说以 末
- 下列四幅图是我市一同学在探究学习活动中绘制的正午日照图(分别选取不同季节的一天),你认为我们l月份期末考试期间的正午日照
- 下列汉字书写完全正确的一项是( ) A.憧憬 跑龙套
- a、b两种色光以相同的入射角从某种介质射向真空,光路如图所示,则以下描述错误的是 A.a光的频率大于b光的频率B.
- 已知函数,则 ( ) A 、 8 B、—8
- 从广州开往北京的列车对铁轨的磨损程度
- 集合A={x|-1≤x<3},B={x|2x-4≥x-2}. (1)求A∩B; (2)若集合C={x|2x+a&g
- (理)数列{an}为等差数列,从{a1,a2,…,a20}中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数
- 英国人麦考利1830年说:“如今我们国家比1790年还穷吗?我们坚决相信,尽管统治者有种种管理不当之处,但英国一直在变得
- 2009年6月13日是我国第四个“文化遗产日”。为体现我国政府高度重视少数民族非物质文化遗产的抢救与保护,展示少数民族传
- 一艘汽船以4 m/s的速度在河面上航行,船上发出一声鸣笛,旅客在3 s后听到前方悬崖反射回来的声音,问悬崖离汽船原来的位
- Tom kept quiet about the accident _______ lose his job
- 若│-5│=4+m,则m= ;若│x-│+(2y+1)2=0,则x2+y3的值= 。
- 将函数f(x)=sin x-cos x的图象向左平移m(m>0)个单位长度,若所得图象对应的函数为偶函数,则m的最
- 如图,矩形中,,,是的中点,点在矩形的边上沿运动,则的面积与点经过的路程之间的函数关系用图象表示大致是下图中的
- 阅读下面短文,根据所需内容在文后第76至第85小题的空格添上适当的单词或短语,并将答案转写到答题卡上。 注意:



