高中 数学
 ,
,  ,则
,则  ;
;  .
.
 ,则
,则  的值为( )
的值为( )
 B .
B .  C .
C .  D .
D . 
 ,则
,则  =( )
=( )
 ,则满足条件的集合
,则满足条件的集合  的个数是( )
的个数是( )
 , 圆
, 圆 :
: , 点
, 点 是圆
是圆 上的动点,
上的动点, 的垂直平分线与
的垂直平分线与 交于点
交于点 , 记
, 记 的轨迹为
的轨迹为 .
.
-
(1) 求
 的方程;
的方程;
-
(2) 设经过点
 的直线
的直线 与
与 交于
交于 ,
,  两点,求证:
两点,求证: 为定值,并求出该定值.
为定值,并求出该定值.

-
(1) 证明:
 ;
;
-
(2) 若
 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 交BD于O.
交BD于O.
-
(1) 求证:平面
 平面PBD;
平面PBD;
-
(2) 延长BC至G,使BC=CG,连结
 .试在棱PA上确定一点E,使
.试在棱PA上确定一点E,使  平面BDE,并求此时
平面BDE,并求此时  的值.
的值.
 在点
在点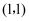 处的切线方程为.
处的切线方程为.

 B .
B .  C .
C .  D .
D . 
某单位有员工120人,其中女员工有72人,为做某项调查,拟采用分层抽样抽取容量为15的样本,则男员工应选取的人数是( )
A.5 B.6 C.7 D.8
本小题![]() 满分12分
满分12分
如图,在直三棱柱ABC—A1B1C1中,AC=1,AB=![]() ,BC=
,BC=![]() ,AA1=
,AA1=![]() 。
。
(I)求证:A1B⊥B1C;
(II)求二面角A1—B1C—B的大小。

已知函数f(x)=sin2x,g(x)=cos![]() ,直线
,直线![]() 与函数
与函数![]() 的图像分别交于M、N两点.
的图像分别交于M、N两点.
(1)当![]() 时,求|MN|的值;
时,求|MN|的值;
(2)求|MN|在![]() 时的最大值.
时的最大值.
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
|
| 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 |
| 6 | |
| 女生 | 10 | ||
| 合计 |
|
| 48 |
已知在全班48人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
参考公式:
 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
正三棱锥S-ABC的外接球半径为2,底边长AB=3,则此棱锥的体积为
A.![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]()
已知![]() 辆汽车通过某一段公路时的时速的频率分布直方图如右图所示:
辆汽车通过某一段公路时的时速的频率分布直方图如右图所示:
(1)求a的值;
(2)估计汽车通过这段公路时时速不小于60km的概率.

1
已知函数 ![]() .
.
(Ⅰ)若函数f(x)在x=1处的切线l过原点,求a的值及切线l的方程;
(Ⅱ)若a=2,且存在t∈R使得f(t)>k,求整数k的最大值.(参考数据:ln5-ln4=0.223).
若 


A .第一象限的角 B .第二象限的角
C .第三象限的角 D .第四象限的角
若![]() ,则
,则![]() 的值为( )
的值为( )
![]()
![]()
![]()
![]()
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
- 下列各组词语中,没有错别字的一组是() A.磋商 举步为艰 仗势欺人 自鸣不凡 B.誊写
- 据史书记载,西周最初分封的七十一国中,姬姓有五十三人,都是周天子的同姓亲属,可见同姓亲属是西周分封的主体。这些同姓亲属受
- 果蝇体细胞内有8个染色体,一个处于减数分裂联会时期的果蝇细胞内四分体数目为 A.16个 B.8
- 下图是“某日某时海平面天气图”,读图完成在图示季节内,可能发生的地理现象有
- 君主专制在从秦到清不断强化的过程中偶有特殊情况,能反映这一情况的是( ) A.战国时期秦国以王为首,统一后秦王称皇帝
- .下列做法中正确的是( ) A.为了节约药品,用剩的药品应放回原试剂瓶 B.为了获得感性认识,可触摸药品或尝药品
- 阅读下面一段话,按要求答题。(4分) 坐在竹伐上,顺流而下,脚下是一条清澈的缓缓溪流,两岸是一片浓密的脉脉翠绿
- Teen Climbing Camp 2010 This 5-day climbing camp is suitabl
- ………你所在的用户组无权浏览除“牛顿运动定律”之外的其它资料,请注册普通会员 或登录………
- 在密闭容器里,A与B反应生成C,其反应速率分别用vA、vB、vC表示,已知2 vB =3 vA、3 vC = 2vB,则
- 3.依次填人下面一段文字横线处的语句,衔接最恰当的一组是 其实,孔子对于读书有自己的看法。 ,
- 已知sin(x+)=-,则sin2x的值等于() (A) (B) (C)- (D)-
- 物质的量浓度相同时,下列既能跟NaOH溶液反应,又能跟盐酸反应的溶液中,pH最大的是()A. Na2CO3溶液 B. N
- Their diet c_________ a lot of fat in the form of butter, cr
- 中国无产阶级的产生先于中国资产阶级,造成这种现象的原因是( ) A. 外国资本主义在中国的早期资本输出 B
- 18. 下列各句中,没有语病、句意明确的一句是( ) A. 不仅是中国、俄罗斯、韩国,就连美国的不少专家也认为,在韩
- 已知关于的函数的图像与坐标轴只有2个交点,求的值.
- 4.下列各句中加点的成语使用恰当的一项是( ) A.90后的思想和理念与老一辈有很大的不同,他们敢于独树一帜,有着不同
- 2010年1月,同在上海的同济大学、上海财经大学、华东师范大学、华东理工大学、上海外国语大学和东华大学等6所高校,各自进
- 下列说法中肯定错误的是( ) A.某原子K层上只有一个电子 B.某原子M层上电子数为L层电子数的4倍 C.某离子M层



